Lista dei politopi regolari

Questa voce elenca i politopi regolari negli spazi euclidei, sferici e iperbolici. La notazione di Schläfli descrive ogni politopo regolare, ed è usata ampiamente nel seguito come abbreviazione per ciascuno di essi.

I politopi regolari sono raggruppati per dimensione e divisi in forme convesse, non convesse e infinite. Le forme non convesse usano gli stessi vertici delle forme convesse, ma hanno facet che si intersecano. Le forme infinite tassellano uno spazio euclideo di dimensione inferiore.

Le forme infinite possono essere estese per tassellare uno spazio iperbolico. Lo spazio iperbolico è come quello normale a brevi distanze, ma le rette parallele divergono a grandi distanze. Questo permette alle figure di vertice di avere difetto d'angolo negativo, come ad esempio componendo un vertice di 7 triangoli equilateri e permettendogli di giacere nello stesso piano. Non può essere fatto nel piano regolare, ma alla giusta scala può essere fatto sul piano iperbolico.

Elenco dei politopi regolari ordinati per dimensione

Dimensione	Convesso	Non convesso	Tassellazioni euclidee convesse	Tassellazioni iperboliche convesse	Tassellazioni iperboliche non convesse
2	∞ poligoni	∞ poligoni stellati	1	1	0
3	5 solidi platonici	4 solidi di Kepler-Poinsot	3 tassellature	∞	∞
4	6 policori convessi	10 policori di Schläfli-Hess	1 alveari	4	0
5	3 5-politopi convessi	0 5-politopi non convessi	3 tassellazioni	5	4
6+	3	0	1	0	0

Politopi regolari bidimensionali

I politopi bidimensionali sono chiamati poligoni. I poligoni regolari sono equilateri e ciclici.

Di solito soltanto i poligoni convessi sono considerati regolari, tuttavia i poligoni stellati, come il pentagramma, possono essere considerati anch'essi regolari. Essi usano gli stessi vertici delle forme convesse, ma si connettono in un percorso alternato che fa il giro più volte prima di ritornare al punto di partenza.

I poligoni stellati andrebbero chiamati non convessi piuttosto che concavi perché gli spigoli che si intersecano non generano nuovi vertici e tutti i vertici stanno su una circonferenza.

Politopi regolari tridimensionali

In 3 dimensioni, i politopi regolari vengono chiamati poliedri:

Un poliedro regolare con simbolo di Schläfli ${\displaystyle \{p,q\}}$ ha facce regolari di tipo ${\displaystyle \{p\}}$, e figura al vertice regolare ${\displaystyle \{q\}}$.

Una figura al vertice (di un poliedro) è un poligono, ottenibile connettendo quei vertici che sono a uno spigolo di distanza da un vertice dato. Per i poliedri regolari, questa figura al vertice è sempre un poligono regolare (e planare).

L'esistenza di un poliedro regolare ${\displaystyle \{p,q\}}$ è vincolata da una disuguaglianza, legata all'angolo di difetto della figura al vertice:

${\displaystyle 1/p+1/q>1/2}$ : Poliedro (esistente nello spazio euclideo tridimensionale)

${\displaystyle 1/p+1/q=1/2}$ : Tassellatura planare euclidea

${\displaystyle 1/p+1/q<1/2}$ : Tassellatura del piano iperbolico

Contando le permutazioni, troviamo 5 forme convesse, 4 forme non convesse e 3 tassellature planari, tutte con poligoni ${\displaystyle \{p\}}$ e ${\displaystyle \{q\}}$ limitati a: ${\displaystyle \{3\},\{4\},\{5\},\{5/2\}}$, e ${\displaystyle \{6\}}$.

Oltre allo spazio euclideo, c'è un insieme infinito di tassellature regolari del piano iperbolico.

Politopi regolari quadridimensionali

I policori regolari con simbolo di Schläfli ${\displaystyle \{p,q,r\}}$ hanno celle di tipo ${\displaystyle \{p,q\}}$, facce di tipo ${\displaystyle \{p\}}$, figure di spigolo ${\displaystyle \{r\}}$, e figure di vertice ${\displaystyle \{q,r\}}$.

• Una figura al vertice (di un policoro) è un poliedro, ottenibile dalla disposizione dei vertici vicini a un vertice dato. Per un policoro regolare, questa figura al vertice è un poliedro regolare.
• Una figura allo spigolo è un poligono, ottenibile dalla disposizione delle facce attorno a uno spigolo. Per i policori regolari, questa figura allo spigolo è un poligono regolare.

L'esistenza di un policoro regolare ${\displaystyle \{p,q,r\}}$ è vincolata dell'esistenza di poliedri regolari ${\displaystyle \{p,q\},\{q,r\}}$.

Ognuno di questi esisterà in uno spazio dipendente dalla seguente espressione:

${\displaystyle \sin \left({\frac {\pi }{p}}\right)\sin \left({\frac {\pi }{r}}\right)-\cos \left({\frac {\pi }{q}}\right)}$

${\displaystyle >0}$ : Policoro di superficie ipersferica (nello spazio quadridimensionale)

${\displaystyle =0}$ : Alveare tridimensionale euclideo

${\displaystyle <0}$ : Alveare tridimensionale iperbolico

Questi vincoli permettono 21 forme: 6 sono convesse, 10 sono non convesse, 1 è un alveare tridimensionale euclideo, e 4 sono alveari iperbolici.

La caratteristica di Eulero ${\displaystyle \chi }$ per i policori è: ${\displaystyle \chi =V+F-E-C}$ ed è 0 per tutte le forme.

Politopi regolari a cinque dimensioni

In cinque dimensioni, un politopo regolare può essere scritto come ${\displaystyle \{p,q,r,s\}}$ dove ${\displaystyle \{p,q,r\}}$ è il tipo di ipercella, ${\displaystyle \{p,q\}}$ è il tipo di cella, ${\displaystyle \{p\}}$ è il tipo di faccia, e ${\displaystyle \{s\}}$ è la figura alla faccia, ${\displaystyle \{r,s\}}$ è la figura allo spigolo, e ${\displaystyle \{q,r,s\}}$ è la figura al vertice.

Un 5-politopo viene chiamato politero, e se infinito (cioè un alveare) un 5-politopo può essere chiamato un

Una figura al vertice (di un 5-politopo) è un policoro, ottenibile dalla disposizione dei vertici vicini a un dato vertice.

Una figura allo spigolo (di un 5-politopo) è un poliedro, ottenibile dalla disposizione delle facce attorno a un dato spigolo.

Una figura alla faccia (di un 5-politopo) è un poligono, ottenibile dalla disposizione delle celle attorno a una data faccia.

Un politopo regolare ${\displaystyle \{p,q,r,s\}}$ esiste solo se ${\displaystyle \{p,q,r\}}$ e ${\displaystyle \{q,r,s\}}$ sono policori regolari.

Lo spazio che riempie si basa sulla seguente espressione:

${\displaystyle {\frac {\cos ^{2}\left({\frac {\pi }{q}}\right)}{\sin ^{2}\left({\frac {\pi }{p}}\right)}}+{\frac {\cos ^{2}\left({\frac {\pi }{r}}\right)}{\sin ^{2}\left({\frac {\pi }{s}}\right)}}}$

${\displaystyle <1}$ : Politopo sferico

${\displaystyle =1}$ : Tassellazione dello spazio euclideo quadridimensionale

${\displaystyle >1}$ : Tassellazione dello spazio iperbolico quadridimensionale

Con questi vincoli si ottengono 3 politopi convessi, zero politopi non convessi, 3 tassellazioni dello spazio euclideo quadridimensionale, e 5 tassellazioni dello spazio iperbolico quadridimensionale.

Politopi convessi classici

Due dimensioni

Il simbolo di Schläfli ${\displaystyle {p}}$ rappresenta un p-agono regolare.

I poligoni regolari convessi sono:

Name	Schläfli Symbol {p}
triangolo equilatero	{3}
quadrato	{4}
pentagono regolare	{5}
esagono regolare	{6}
eptagono regolare	{7}
ottagono regolare	{8}
nonagono regolare	{9}
decagono regolare	{10}
endecagono regolare	{11}
dodecagono regolare	{12}
...n-agono regolare	{n}
apeirogono	{∞}

{2}

{3}

{4}

{5}

{6}

{7}

{8}

{9}

{10}

{11}

{12}

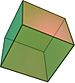
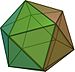
Un digono, {2}, può essere considerato un poligono regolare degenere.

Tre dimensioni

I cinque poliedri regolari convessi vengono chiamati solidi platonici. (Per ciascun vertice è data la figura al vertice corrispondente.)

Nome	Simbolo di Schläfli {p,q}	Facce {p}	Spigoli	Vertici {q}	χ	Symmetria	Duale
Tetraedro	{3,3}	4 {3}	6	4 {3}	2	Td	Autoduale
Cubo (esaedro)	{4,3}	6 {4}	12	8 {3}	2	Oh	Ottaedro
Ottaedro	{3,4}	8 {3}	12	6 {4}	2	Oh	Cubo
Dodecaedro	{5,3}	12 {5}	30	20 {3}	2	Ih	Icosaedro
Icosaedro	{3,5}	20 {3}	30	12 {5}	2	Ih	Dodecaedro

{3,3}	{4,3}	{3,4}	{5,3}	{3,5}

In geometria sferica, l'osoedro (simbolo di Schläfli {2,n}) e il diedro (simbolo di Schläfli {n,2}) possono essere considerati poledri regolari (tassellature della sfera).

Quattro dimensioni

I 6 policori regolari sono i seguenti:

Name	Simbolo di Schläfli {p,q,r}	Celle {p,q}	Facce {p}	Spigoli {r}	Vertici {q,r}	χ	Duale {r,q,p}
5-cella (Pentacoro)	{3,3,3}	5 {3,3}	10 {3}	10 {3}	5 {3,3}	0	Autoduale
8-cella (Ipercubo tesseratto)	{4,3,3}	8 {4,3}	24 {4}	32 {3}	16 {3,3}	0	16-cella
16-cella	{3,3,4}	16 {3,3}	32 {3}	24 {4}	8 {3,4}	0	Ipercubo tesseratto
24-cella	{3,4,3}	24 {3,4}	96 {3}	96 {3}	24 {4,3}	0	Autoduale
120-cella	{5,3,3}	120 {5,3}	720 {5}	1200 {3}	600 {3,3}	0	600-cella
600-cella	{3,3,5}	600 {3,3}	1200 {3}	720 {5}	120 {3,5}	0	120-cella

5-cella	8-cella	16-cella	24-cella	120-cella	600-cella
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}
Proiezioni ortografiche reticolari
Proiezioni ortografiche solide (centrate nelle celle)
Inviluppo tetraedrale	Inviluppo cubico	Inviluppo ottaedrico	Inviluppo cubottaedrale	Inviluppo di triacontaedro rombico troncato	Inviluppo pentacisdodecaedrico
Diagrammi di Schlegel reticolari (Proiezione prospettica)
(centrato nella cella)	(centrato nella cella)	(centrato nella cella)	(centrato nella cella)	(centrato nella cella)	(centrato nel vertice)
Proiezioni stereografiche (Ipersferiche) reticolari

Politopi finiti non convessi - politopi stellati

Due dimensioni

Esistono infiniti politopi regolari non-convessi a due dimensioni, i cui simboli di Schläfli consistono di numeri razionali {m/n}. Essi vengono chiamati poligoni stellati.

In generale, per ogni numero naturale n, ci sono poligoni stellati a n punte con simboli di Schläfli {n/m} per ogni m tale che m < n/2 (o equivalentemente {n/m}={n/(n-m)}) e m and n sono coprimi.

Nome	Simbolo di Schläfli{n/m}
pentagramma	{5/2}
eptagramma	{7/2}, {7/3}
octagramma	{8/3}
enneagramma	{9/2}, {9/4}
decagramma	{10/3}
endecagramma	{11/2} {11/3}, {11/4}, {11/5}
dodecagramma	{12/5}
...n-agrammi	{n/m}

{5/2}

{7/2}

{7/3}

{8/3}

{9/2}

{9/4}

Dimensioni superiori

Non ci sono politopi regolari non-convessi in cinque o più dimensioni.

Tassellazioni

Apeirotopi

Un apeirotopo è, come ogni altro politopo, una ipersuperficie illimitata. La differenza è che, mentre l'ipersuperficie di un politopo si ricurva su di sé per racchiudere un volume finito dell'iperspazio, un apeirotopo semplicemente non si ferma mai.

Alcuni considerano gli apeirotopi semplicemente come un tipo particolare di politopo, mentre altri li considerano di tutt'altra specie.

Politopi astratti

Bibliografia

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V, p212-213)

Voci correlate

• Poligono
  • Poligono regolare
  • Poligono stellato
• Poliedro
  • Poliedro regolare (i 5 solidi platonici regolari e i 4 solidi di Keplero-Poinsot)
    • Poliedro uniforme
• Policoro (matematica)
  • Policoro regolare convesso (6 policori regolari)
    • Policoro uniforme
  • Policoro di Schläfli-Hess (10 policori regolari stellati)
• Tassellazioni
  • Ricoprimento di poligoni regolari
  • Alveari uniformi convessi
• Politopo regolare
  • Politopo uniforme

Collegamenti esterni

• I solidi platonici, su math.utah.edu. URL consultato il 29 settembre 2007 (archiviato dall'url originale il 9 marzo 2021).
• I poliedri di Kepler-Poinsot, su georgehart.com.
• Sviluppi di politopi regolari quadridimensionali, su weimholt.com. URL consultato il 29 settembre 2007 (archiviato dall'url originale il 17 luglio 2011).
• Glossario multidimensionale (Vedi Hexacosichoron e Hecatonicosachoron)
• Visualizzatore di politopi, su geocities.com.
• Politopi e raggruppamento ottimale di p punti in sfere n-dimensionali, su presh.com. URL consultato il 29 settembre 2007 (archiviato dall'url originale il 15 giugno 2006).
• Un atlante di piccoli politopi regolari, su abstract-polytopes.com.