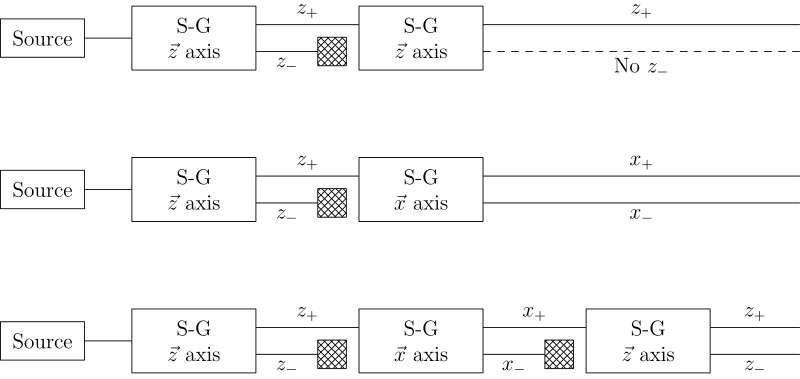
it Esperimento di Stern-Gerlach

In meccanica quantistica, l'esperimento di Stern-Gerlach^[1], che prende il nome da Otto Stern e Walther Gerlach, è un importante esperimento del 1922 sulla deflessione delle particelle, spesso preso come esempio per illustrare i principi alla base della meccanica quantistica. Può essere usato per dimostrare che elettroni e atomi hanno proprietà quantistiche intrinseche, e come la misura di un sistema quantistico influenzi il sistema in esame.

Teoria di base e descrizione

Otto Stern e Walther Gerlach escogitarono un esperimento per determinare se le particelle avessero un momento angolare intrinseco. In un sistema classico, come un pianeta in orbita intorno a una stella, il pianeta ha un momento angolare dato dalla rivoluzione intorno alla stella e dalla rotazione rispetto al proprio asse (spin). Se si considera un elettrone come un dipolo magnetico classico generato dalla sua carica rapidamente rotante, si osserverà la precessione di Larmor in un campo magnetico, a causa del momento torcente che il campo esercita sul dipolo.

Se la particella si muove in un campo magnetico omogeneo, le forze esercitate sulle estremità opposte del dipolo si cancellano a vicenda e la traiettoria della particella non è modificata. Se l'esperimento è eseguito con elettroni, un campo magnetico di intensità appropriata e orientato trasversalmente alla traiettoria della particella viene usato per compensare la tendenza di ogni particella carica a ruotare nel suo percorso attraverso il campo magnetico (vedi anche ciclotrone); con questa compensazione si può ignorare l'effetto della carica elettrica. L'esperimento di Stern-Gerlach può essere condotto usando particelle elettricamente neutre ottenendo le stesse conclusioni, in quanto è progettato per la misura del solo momento angolare, e non per la misura di fenomeni elettrici.

Se la particella attraversa un campo magnetico non omogeneo, la forza a un'estremità del dipolo sarà leggermente maggiore di quella all'estremità opposta; questo causa la deflessione della particella. La direzione in cui le particelle sono deflesse è indicata convenzionalmente con z. Se le particelle sono classiche e rotanti su loro stesse ("dotate di spin"), allora la distribuzione del loro momento angolare di spin è casuale e ogni particella sarebbe deflessa verso l'alto o il basso (verso valori positivi o negativi di z) di una differente quantità, producendo una distribuzione regolare sullo schermo di un rivelatore. Invece, le particelle che passano attraverso il campo magnetico sono deflesse o in alto o in basso di una quantità precisa. Questo indica che il momento angolare di spin è quantizzato, cioè assume solo valori discreti: non c'è quindi una distribuzione continua di possibili valori del momento angolare.

Gli elettroni sono particelle con valore del modulo del vettore di spin ½. Hanno quindi solo due possibili valori della proiezione (o componente) lungo un asse, del momento angolare, chiamati spin up e down; il valore esatto della componente lungo la direzione z è quindi $+\hbar /2$ e $-\hbar /2$ . Se questo valore fosse il risultato della rotazione delle particelle su sé stesse, analoga alla rotazione dei pianeti, la velocità di rotazione dovrebbe essere maggiore di quella della luce: tale spiegazione è dunque errata^[2]. Inoltre, se si usa un modello in cui le particelle sono puntiformi, cioè non hanno estensione, non è possibile definire un momento di rotazione su sé stesse. Lo spin quindi non è legato alla rotazione ed è un fenomeno puramente quantistico; per questo motivo è definito come "momento angolare intrinseco".

Anche protoni e neutroni hanno due possibili valori di spin, e sono particelle composte da tre quark ciascuna, che sono essi stessi particelle con spin ½. Altre particelle possono avere un diverso numero di valori possibili. Il numero di valori possibili è dato da $2s+1$ , dove s è il valore del modulo del vettore di spin. Lo spin s è semi-intero per i fermioni e intero per i bosoni.

Per descrivere l'esperimento con particelle con spin ½ matematicamente è più semplice utilizzare la notazione bra-ket di Dirac. Quando una particella passa attraverso il dispositivo di Stern-Gerlach viene "osservata". L'osservazione in meccanica quantistica è equivalente alla misura. Lo strumento di osservazione è il rivelatore, e in questo caso possiamo osservare uno dei due possibili valori, o spin up o spin down; questi sono descritti con il numero quantico del momento angolare generico j, che può assumere i due valori $+\hbar /2$ o $-\hbar /2$ . L'operazione di misura è descritta da un operatore $J_{z}$ . In termini matematici

|\psi \rangle =c_{1}\left|\psi _{j=+{\frac {\hbar }{2}}}\right\rangle +c_{2}\left|\psi _{j=-{\frac {\hbar }{2}}}\right\rangle .

I coefficienti costanti c₁ e c₂ sono numeri complessi. Elevando al quadrato i loro valori assoluti $\scriptstyle |c_{1}|^{2}$ e $\scriptstyle |c_{2}|^{2}$ si determina la probabilità che nello stato $|\scriptstyle \psi \rangle$ sia assunto uno dei due possibili valori di j. I coefficienti devono anche essere normalizzati in modo che la probabilità complessiva sia 1. Comunque questa informazione non è sufficiente per determinare i valori di c₁ e c₂, in quanto sono numeri complessi. La misura fornisce quindi solo i valori assoluti dei coefficienti.

Esperimenti di Stern-Gerlach in sequenza

Se si combinano alcuni apparati di Stern–Gerlach si può vedere chiaramente che non agiscono come semplici selettori, ma alterano lo stato osservato secondo le leggi della meccanica quantistica; tale fenomeno è analogo alla polarizzazione della radiazione elettromagnetica); come illustrato nella figura seguente, ogni apparato agisce infatti come un filtro polarizzatore:

Storia

Targa commemorativa dell'esperimento all'istituto di Francoforte

L'esperimento fu eseguito nel 1922 a Francoforte da Otto Stern e Walther Gerlach. In quel periodo Stern era un assistente di Max Born all'Istituto di Fisica Teorica della Johann Wolfgang Goethe-Universität, mentre Gerlach era assistente presso l'Istituto di Fisica Sperimentale della stessa università.

All'epoca dell'esperimento, il modello più accreditato per la descrizione dell'atomo era il modello atomico di Bohr secondo il quale gli elettroni orbitavano attorno al nucleo carico positivamente. Questo poteva avvenire solo in alcuni specifici orbitali o livelli di energia di natura discreta (ad esempio tra il primo e il secondo livello, che erano ben separati, non poteva esisterne un altro, perciò l'elettrone si trovava o al livello energetico inferiore o al livello superiore, ma mai in mezzo). L'esperimento di Stern e Gerlach aveva lo scopo di verificare l'ipotesi di Bohr-Sommerfield secondo cui il momento angolare di un atomo è quantizzato. Eseguirono l'esperimento utilizzando degli atomi di argento^[3].

Si può notare come l'esperimento fu eseguito diversi anni prima che Uhlenbeck e Goudsmit formulassero le loro ipotesi sull'esistenza dello spin di una particella. Benché il risultato dell'esperimento di Stern-Gerlach fu in seguito trovato essere in accordo con le predizioni della meccanica quantistica di uno spin ½, esso può essere visto anche come una conferma della "vecchia" teoria di Bohr-Sommerfeld^[4].

Nel 1927, T.E. Phipps e J.B. Taylor riprodussero l'esperimento utilizzando atomi di idrogeno, per dissipare il dubbio che il tutto fosse dovuto all'uso di atomi di argento^[5] (nel 1926 l'equazione di Schrödinger non relativistica aveva predetto, sbagliando, che il momento magnetico dell'idrogeno fosse nullo; per ovviare a questo problema, Pauli introdusse "a mano" le tre matrici di spin che oggi portano il suo nome, che Dirac nel 1928 dimostrò essere intrinseche nella sua equazione relativistica^[6]).

Impatto

L'esperimento di Stern-Gerlach ha avuto una grande influenza sulla fisica moderna:

Nel decennio seguente è stato mostrato, usando tecniche simili, che anche i nuclei di alcuni atomi hanno momento angolare quantizzato. L'interazione tra questo momento angolare nucleare con lo spin dell'elettrone è responsabile della struttura iperfine osservata negli spettri.
Negli anni trenta, usando una versione estesa dell'apparato di Stern-Gerlach, Isidor Rabi e colleghi hanno mostrato che usando un campo magnetico variabile è possibile cambiare lo stato del momento magnetico. La serie di esperimenti culminò nel 1937, quando fu scoperto che le transizioni di stato possono essere indotte usando campi variabili nel tempo o onde radio. Le cosiddette "oscillazioni di Rabi" sono alla base del funzionamento dell'imaging a risonanza magnetica, tecnica usata in medicina.
Più tardi Norman F. Ramsey modificò l'apparato di Rabi per aumentare il tempo di interazione con il campo. L'estrema sensibilità dovuta alla frequenza della radiazione rende questo accorgimento molto utile per tenere il tempo con accuratezza, ed è ancora oggi usato negli orologi atomici.
All'inizio degli anni sessanta Ramsey e Daniel Kleppner usarono un apparato Stern-Gerlach per produrre un raggio di idrogeno polarizzato come sorgente di energia per un maser a idrogeno, ancora oggi uno dei più diffusi orologi atomici.
L'osservazione diretta dello spin è una delle prove principali della quantizzazione.
L'esperimento di Stern-Gerlach è divenuto un paradigma della misura quantistica, in particolare perché si è ritenuto che soddisfacesse lo schema di misura di Von Neumann. In realtà, in accordo con le più recenti conoscenze, basate sulla descrizione quantomeccanica dell'influenza di un campo magnetico non omogeneo^[7], ciò è vero solo in prima approssimazione: lo schema di Von Neumann può essere rigorosamente rispettato solo da un campo magnetico omogeneo; quindi, risulta incompatibile con il funzionamento dell'apparecchio di Stern-Gerlach per misurare lo spin delle particelle.

Note

^ Walther Gerlach & Otto Stern, "Das magnetische Moment des Silberatoms", Zeitschrift für Physik 9, 353-355 (1922).
^ Sin-itiro Tomonaga, The Story of Spin, University of Chicago Press, 1997, ISBN 0-226-80794-0. p. 35.
^ Otto Stern, "Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld", Zeitschr. f. Physik 7, 249-253 (1921).
^ F. Weinert, Wrong theory—right experiment: The significance of the Stern–Gerlach experiments, in Studies in History and Philosophy of Modern Physics, 26B, 1995, pp. 75−86, DOI:10.1016/1355-2198(95)00002-B.
^ T.E. Phipps e J.B. Taylor, The Magnetic Moment of the Hydrogen Atom, in Physical Review, vol. 29, n. 2, 1927, pp. 309–320, Bibcode:1927PhRv...29..309P, DOI:10.1103/PhysRev.29.309.
^ Henok A., Introduction to Applied Modern Physics, Lulu.com, 2002, p. 76, ISBN 1-4357-0521-1.
^ M.O. Scully, W.E. Lamb e A. Barut, On the theory of the Stern–Gerlach apparatus, in Foundations of Physics, vol. 17, 1987, pp. 575–583, DOI:10.1007/BF01882788.