|
Diedro (poliedro)
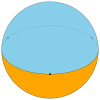
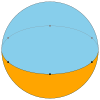
Un diedro è un tipo di poliedro costituito da due facce poligonali che condividono gli stessi n spigoli. Nello spazio euclideo tridimensionale il diedro rappresenta un caso degenere di poliedro e le sue facce sono piatte, nello spazio sferico tridimensionale, invece, un diedro con facce piatte può essere visto come una lente e un suo tipico esempio è il dominio fondamentale di uno spazio lenticolare .[1] In letteratura i diedri sono talvolta chiamati anche biedri[2] e poliedri piatti.[3] Il diedro può esistere nella sua forma non degenere come poliedro sferico, e quindi come tassellatura sferica, con le sue due facce di n lati a coprire la sfera, essendo ognuna di esse una semisfera, e con i vertici su una circonferenza massima posta all'equatore della sfera. In questo caso il diedro è regolare se i sopraccitati vertici sono tutti equidistanti. Il poliedro duale di un diedro n gonale è un osoedro n-gonale, un poliedro in cui le n facce digonali a forma di fuso sferico condividono i due vertici. Come poliedro a facce pianeUn diedro può essere considerato un prisma degenere le cui due basi poligonali e planari di n lati sono collegate "faccia a faccia", in modo che l'oggetto risultante non abbia profondità. I poligoni devono essere congruenti, ma sovrapposti in modo tale che uno sia l'immagine speculare dell'altro. Questo vale solo se la distanza tra le due facce è zero; per una distanza maggiore di zero, le facce sono poligoni infiniti (un po' come le facce di digonali di un osoedro apeirogonale, con una larghezza maggiore di zero, sono strisce infinite). L'esistenza dei diedri può essere desunta dal teorema di unicità di Alexandrov, che identifica le distanze sulla superficie di qualsiasi poliedro convesso come localmente euclidee tranne che in un numero finito di punti con difetto angolare positivo che ha un valore totale di 4π. Questa qualificazione vale anche per le distanze sulla superficie di un diedro, quindi l'affermazione del teorema di Alexandrov richiede che i diedri siano considerati poliedri convessi.[4] Alcuni diedri appaiono invece come membri estremi di altre famiglie di poliedri: ad esempio, un prisma con basi digonali sarebbe un diedro quadrato, mentre una piramide con una base digonale sarebbe un diedro triangolare. Un diedro regolare costituito da due poligoni regolari, ognuno con simbolo di Schläfli {n}, ha simbolo di Schläfli {n,2}.[5] Come tassellatura sfericaUn diedro sferico è composto da due poligoni sferici che condividono gli stessi n vertici, siti su una circonferenza massima equatoriale, e che costituiscono ognuno una semisfera. Nel caso in cui i suddetti vertici siano equidistanti sulla circonferenza massima, allora il diedro sferico è regolare. Il poliedro regolare {2,2} è auto-duale essendo sia un diedro che un osoedro.
Diedro apeirogonalePer n tendente a infinito, un diedro n-gonale diventa un diedro apeirogonale in forma di tassellatura bidimensionale: DitopiCosì come i poliedri sono politopi tridimensionali, allo stesso modo un diedro è un particolare ditopo a tre dimensioni. Un ditopo regolare a n dimensioni, con n>3, e rappresentato in notazione di Schläfli come {p,...,q,r,2} ha due faccette, {p,...,q,r}, che condividono tutte le (n-1)-faccette aventi come simbolo di Schläfli {p,...,q}.[6] Note
Altri progetti
Collegamenti esterni |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||