Logarléc

Logarléc

A logarléc (logaritmikus számolóléc) egy egyszerű kivitelű, mechanikus működésű analóg számológép, amely lehetővé teszi különböző matematikai műveletek gyors, 3-4 számjegy pontosságú elvégzését.

Szabványos logarlécek esetében az elvégezhető műveletek általában a következők: szorzás, osztás, négyzetre és köbre emelés, négyzet, illetve köbgyök vonása, logaritmusszámítás, trigonometriai függvények kiszámítása.

A logarléc ablaka

Működési elve

Összeadás

Ha két vonalzót egymás mellett elcsúsztatunk, akkor gyorsan tudunk két számot (távolságot) összeadni:

${\displaystyle x+y=z}$ :

Összeadás vonalzókkal

A logarléc működésének alapelve, hogy a számok szorzatát a számok logaritmusának összegzésével, a számok hányadosát a számok logaritmusának különbségével számítjuk ki.

A logarléc alapja két, egymáson elcsúsztatható logaritmikus skála. Ezt egészítik ki további skálák és egy átlátszó mozgatható ablak, amelyen hajszálvonalak segítik a skálákon található értékek pontos beállítását és leolvasását.

Szorzás

Két szám összeszorzásához a nyelv (mozgatható skála) kezdő értékét a fix skálán a szorzandó értékéhez kell mozgatni, és ezt követően a nyelven megkeresni a szorzót; a vele szemben a fix skálán található érték lesz a szorzat értéke.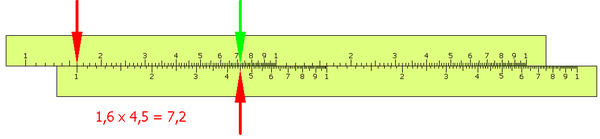

${\displaystyle \lg(x)+\lg(y)=\lg(xy)}$

Szorzás

A szorzat értékének meghatározásához nem elegendő a skála leolvasása, a logarléc használójának fejben utánaszámolva meg kell állapítania a szorzat nagyságrendjét. Az ábra példáján 1,6 × 4,5 szorzatához ugyanúgy kell beállítani a skálát, mint 160 × 45 vagy 0,16 × 0,45 esetén.

Ha a skálák 1–10-ig készültek, könnyen kifuthatunk a tartományból. Például 2 × 7 = 14. Ilyenkor vagy olyan skálát használunk, amely 1-100-ig van beosztva, mint az ábrán, vagy a nyelv másik irányba való mozgatásával keressük meg a szorzatot.

Osztás

Osztáskor a nyelven (mozgó skálán) meg kell keresni az osztót, ezt szembe kell állítani a fix skálán az osztandóval, és a nyelv kezdeti értékénél találjuk a fix skálán a hányados értékét.

${\displaystyle \lg(x)-\lg(y)=\lg(x/y)}$

Más skálák

Az alapvető logaritmikus skálákon kívül a gyakorlatban használatos logarlécek más skálákat is tartalmaznak.

A kétszeres léptékű és egyszeres léptékű logaritmikus skálák összevetésével könnyen lehet négyzetre emelni és négyzetgyököt vonni. Arra azonban vigyázni kell, hogy például 4 és 40 négyzetgyökét máshol kell keresni a felső skálán. Négyzetgyökvonásnál a számot a tizedesvesszőtől számítva két számjegyből álló csoportokra bontjuk, és ahol a felosztás már nem folytatódhat, ott látjuk, melyik mezőben kell keresni a négyzetgyököt.

Háromszoros léptékű logaritmikus skálával ehhez hasonlóan köbgyököt lehet vonni. Gyakorlati számításokhoz fontosak a szögfüggvények, a szinusz, koszinusz és tangens skálák. Kis szögek szinusz és tangens skálája is található a legtöbb logarlécen.

Négyzetre emelés-négyzetgyök vonás

A fordított logaritmikus skála 1/x számítását könnyíti meg.

Lineáris skála segítségével a számok 10-es alapú logaritmusát lehet megkeresni, log-log skála pedig a természetes alapú logaritmus keresését és tetszőleges hatványozást tesz lehetővé.

A leggyakrabban használatos skálák

A, B	Kétszeres léptékű logaritmikus skálák, az előbbi a testen, az utóbbi a nyelven. Négyzetre emelésre és négyzetgyökvonásra használatosak.
C, D	A klasszikus logaritmikus skálák.
K	Háromszoros léptékű logaritmikus skála.
CF, DF	A szimpla logaritmikus skála π-vel szorozva.
CI, DI, DIF	Logaritmikus skála reciproka. Gyakorlatilag a logaritmus skála tükrözöttje.
S	Szinusz skála általában 6°-tól 90°-os értékekig.
T1, T2	Tangens skálák, az előbbi 6° és 45°, az utóbbi 45° és 84° között.
ST, SRT	Skála kis szögek tangensének, szinuszának és fok-radián átváltásának számításához.
L	A C és a D skála logaritmusa. Gyakorlatilag egy lineáris skála 0 és 1 között.
LLn	3 vagy 4 db log-log skála. Könnyen számítható vele valós számokkal történő hatványozás.
Ln	Természetes alapú logaritmus skála, ez is lineáris 0 és 2,3 között.

Skálák a K&E 4081-3 logarléc elején és hátulján

Gyakorlati kivitel

Körlogarléc

A logarléceket régebben fából, majd fa és műanyag kombinációjából készítették, legújabban teljesen műanyagból vagy fémből állnak. A fém logarlécek ugyan lehetővé teszik a pontosság növelését, de a csillogó felület és a fémes szín miatt a leolvasás nehezebb és így használatuk fárasztóbb. A közönséges logarlécek leolvasási pontossága általában két számjegy és a harmadikat a felhasználó megbecsülte, a speciális logarlécek pontossága ennek kétszerese is lehet. Európában a szabványos hossz 25 cm, emellett készültek 12,5 cm-es (zseb-) és 50 cm-es (irodai) logarlécek is. Angolszász országokban a szabványos logarléc hossza 10, 5, illetve 12,5 hüvelyk (25,4, 12,7 és 31,8 cm).

A skáláról való kifutás elkerülhető az ún. körlogarléccel, ahol a skálákat két koncentrikus kör alakú tárcsára viszik fel. Ennek előnye még, hogy hosszabb skálát harmad akkora főméretekkel lehet készíteni, mint a közönséges logarlécekkel. Ennek ellenére a logarlécek túlnyomó többsége egyenes típusú.

Különböző szakmák egyedi céljainak megfelelő speciális logarléceket is készítettek, így például létezett különböző, mérnököknek, bankoknak és pénzügyi célokra szánt logarléc, de például a II. világháború amerikai bombázópilótái is használtak különleges logarléceket.

Története

A logarlécet 1620-1630 között találták fel, miután John Napier publikálta a logaritmusról szóló alapvető művét. Az oxfordi egyetemen Edmund Gunter feltalált egy eszközt, mely egy logaritmikus skálából és mérőeszközökből állt és amellyel szorozni és osztani lehetett. 1630-ban a cambridge-i William Oughtred készített egy körlogarlécet, és 1632-ben egyesítette találmányát Gunter eszközével, ezzel létrejött a mai értelemben vett logarléc. Oughtred sokáig nem publikálta találmányát, hasonlóan a kortárs Newtonhoz, aki forradalmian új fizikai elméleteit évekig nem merte nyilvánosságra hozni, és később kemény harcot folytatott az elsőbbségért egy korábbi tanítványával, Richard Delamainnel.

1722-ben Warner bevezette a négyzet- és köbskálát, 1755-ben Everard az inverz skálát (1/x), 1815-ben pedig Peter Roget feltalálta a log-log skálát. A 19. században a logarléc használata széles körben elterjedt Európában. A mérnöki számítások túlnyomó részét logarléc segítségével végezték. Ehhez természetesen olyan számítási eljárásokra volt szükség, melyek nem voltak érzékenyek a kerekítési hibára.

Az 1970-es, 1980-as években a logarléc végleg elavult, felváltották a különböző tudományos kalkulátorok, 1974-től a logarlécek gyártói sorozatban mentek csődbe.[1][2][3][4] Ezzel az emberiség kultúrájának egy kiemelkedő találmánya került múzeumba.

A legutolsó speciális logarlécek az amerikai Apollo-program számára készültek, és a programban részt vevő űrhajósok használták azokat.

A logarlécet mára az elektronikus eszközök teljesen kiszorították, csak múzeumokban és idősebb mérnökök gyűjteményeiben lelhetők fel.

Előnyök

A bankokban régen használt kamathenger, a logarléc módosított formája. Akár 7 tizedesjegyig tudja mutatni az értékeket

• A logarléc korlátozott pontossága nem mindig hátrány. A legtöbb mérnöki számításnál a kiinduló adatok pontossága nem nagyobb annál, mint amit a logarléc nyújt. A számológép 7–9 jegyű pontossága azt az illúziót kelti, hogy nagyon pontos eredményre jutunk, holott a bemenő adatok valójában pontatlanok. Ettől a hibás illúziótól megóv a logarléc használata.
• A logarléccel való munka megköveteli a nagyságrendek fejben történő ellenőrzését. Ez nagy ellenőrzési biztonságot ad a számítások során: aki logarléccel dolgozik, nem követ el olyan jellegű nagyságrendi hibát, ami a modern számítástechnikában (adatok elütése miatt) könnyen bekövetkezhet.
• A gyakorlati számítást igen sok apró fogás könnyíti és gyorsítja logarléccel. Például, ha egy számot sok számmal akarunk egymást követően szorozni, a skálát elég egyszer beállítanunk, utána csak az ablakot kell mozgatni, és az eredményeket leolvasni.
• Mivel a logarléc működése mechanikus, nem igényel áramforrást.
• A logarlécek annyira szabványosak, hogy egy új logarléc használatához semmiféle utasítás nem szükséges.

Hátrányok

Ez a szakasz egyelőre üres vagy erősen hiányos. Segíts te is a kibővítésében!

• A számítás pontossága függ a logarléc hosszától.[5]

Általánosítások

Az eddig ismertetett logaritmikus skálák helyett a csúszkákra tetszőleges más skálákat helyezve más képleteket is kiszámolhatunk gyorsan.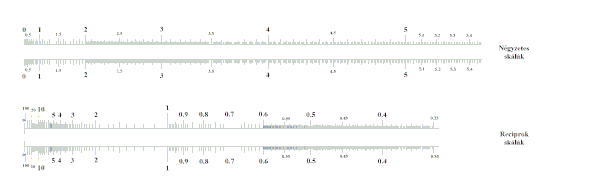

Reciprok és négyzetes skálák

Például, négyzetes skálákkal az ${\displaystyle x^{2}+y^{2}=z^{2}}$ összefüggés, reciprok skálákkal az ${\displaystyle {\frac {1}{x}}+{\frac {1}{y}}={\frac {1}{z}}}$ összefüggés alapján kereshetjük meg ${\displaystyle z}$-t ${\displaystyle x}$ és ${\displaystyle y}$ ismeretében, egyetlen léceltolással.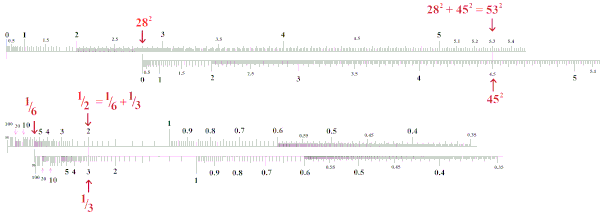

A reciprok és négyzetes skálák használata

A reciprok és négyzetes skálák használata: erről részletesebben itt[6][7][8] olvashatunk.

Jegyzetek

A Wikimédia Commons tartalmaz Logarléc témájú médiaállományokat.

1. Writing and reading across the curriculum. Little, Brown, 273. o. (1982) „Then, just a decade ago, the invention of the pocket calculator made the slide rule obsolete almost overnight...” 
2. e: The Story of a Number. Princeton University Press, 16. o. (2009). ISBN 9780691141343 „Then in the early 1970s the first electronic hand-held calculators appeared on the market, and within ten years the slide rule was obsolete.” 
3. Inventions that Changed the World. Futura, 157. o. (2007). ISBN 9780708807866 „With the invention of the calculator the slide rule became instantly obsolete.” 
4. Beyond calculation: the next fifty years of computing. Springer, xiv. o. (1998). ISBN 9780387985886 „The first hand calculator appeared in 1972 and made the slide rule obsolete overnight.” 
5. A logarléc
6. Szalkai István: Mit tudhat egy számolóléc?, KöMaL 1977. http://math.uni-pannon.hu/~szalkai/Szalkai-1977-KoMaL.pdf, http://db.komal.hu/scan/1977/04/97704146.g4.png http://db.komal.hu/scan/1977/04/97704151.g4.png
7. Szalkai,I.: General Two-Variable Functions on the Slide Rule, Journal of the Oughtred Society, 27:1, Spring  2018, pages 14-18. http://www.oughtred.org/jos/pages/JOS_2018_Vol_27_1_TOC.jpg
8. Szalkai,I.: General Two-variable Functions on the Slide-rule, http://arxiv.org/abs/1612.03955

Források

• Sárközy Zoltán: Műszaki táblázatok és képletek. Műszaki Könyvkiadó, Budapest, 1977. ISBN 963-10-1241-7
• www.arithmomuseum.com: Virtuális logarléc-múzeum. www.arithmomuseum.com. (Hozzáférés: 2022. május 27.)

További információk

Online szimulátorok:

• Sag Milling's Online Sliderule – Teljesen működőképes logarléc
• Körlogarléc (Flash) – A Center for Technology and Teacher Education, University of Virginia-tól
• Logarléc Java szimulációja– Szerző: Andrew Davie