Létragráf

Létragráf
Az L8 létragráf
Csúcsok száma	2n
Élek száma	3n−2
Derékbőség	4, ha n>1
Kromatikus szám	2
Élkromatikus szám	3, ha n>2 2, ha n=2 1, ha n=1
Egyéb	Egységtávolsággráf Hamilton-körű Síkbarajzolható Páros
Jelölés	Ln

A matematika, azon belül a gráfelmélet területén az L_n-nel jelölt létragráf (ladder graph) egy 2n csúccsal és 3n−2 éllel rendelkező összefüggő, irányítatlan, síkbarajzolható gráf.[1]

A létragráf előállítható két útgráf Descartes-szorzataként, amennyiben az egyik útgráf csak egyetlen éllel rendelkezik: L_n,1 = P_n × P₂.[2][3]

Tulajdonságok

A konstrukciós szabály alapján nyilvánvaló, hogy az L_n létragráf a G_2,n rácsgráffal izomorf, és valóban emlékeztet egy n fokkal rendelkező létrára. Rendelkezik Hamilton-körrel, girthparamétere 4 (ha n>1), élkromatikus száma pedig 3 (ha n>2). A gráf négy sarki helyzetű csúcsának fokszáma 2, a többi csúcsé 3. Az L_n létragráf teljes párosításainak száma megegyezik az F_n+1 Fibonacci-számmal.

A létragráf kromatikus száma 2, kromatikus polinomja pedig 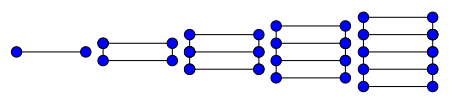${\displaystyle (x-1)x(x^{2}-3x+3)^{(n-1)}}$.

Az L₁, L₂, L₃, L₄ és L₅ létragráfok.

• 
  A létragráf kromatikus száma 2.

Létrafok-gráf

Néha létragráf alatt az n × P₂ létrafok-gráfot (ladder rung graph) értik, azaz n db 2 hosszúságú útgráf diszjunkt unióját.

Az LR₁, LR₂, LR₃, LR₄ és LR₅ létrafok-gráfok.

Körkörös létragráf

A létragráf négy 2 fokszámú csúcsát egyenesen összekötve, avagy egy n≥3 hosszúságú kör és egy él Descartes-szorzatával a körkörös létragráf (circular ladder graph), CL_n áll elő.[4]

Szimbolikusan: CL_n = C_n × P₁.

A körkörös létragráf 2n csúccsal és 3n éllel rendelkező, összefüggő síkbarajzolható gráf Hamilton-körrel, de kizárólag akkor páros, ha n páros.

A körkörös létragráfok a hasábok poliédergráfjai, ezért hasábgráfnak is nevezik őket.

Körkörös létragráfok:

CL3

CL4

CL5

CL6

CL7

CL8

Möbius-létragráf

Bővebben: Möbius-létra

Egy létragráf négy 2 fokszámú csúcsát keresztben összekötve 3-reguláris gráf jön létre, amit Möbius-létrának neveznek.

Az M₁₆ Möbius-létra két nézete.

Fordítás

• Ez a szócikk részben vagy egészben a Ladder graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
• Ez a szócikk részben vagy egészben a Leitergraph című német Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

1. Weisstein, Eric W.: Ladder Graph (angol nyelven). Wolfram MathWorld
2. Hosoya, H. and Harary, F. "On the Matching Properties of Three Fence Graphs." J. Math. Chem. 12, 211-218, 1993.
3. Noy, M. and Ribó, A. "Recursively Constructible Families of Graphs." Adv. Appl. Math. 32, 350-363, 2004.
4. (2013. szeptember 1.) „Total Embedding Distributions of Circular Ladders”. Journal of Graph Theory 74 (1), 32–57. o. DOI:10.1002/jgt.21690.