|
Tas binomialEn informatique, un tas binomial est une structure de données assez proche du tas binaire, mais qui permet aussi de fusionner deux tas rapidement. Ainsi, il supporte les opérations suivantes, toutes en O(log n) :
Le tas binomial est donc une implémentation du type abstrait tas fusionnable, c'est-à-dire une file à priorités permettant des opérations de fusion. Notion d'arbre binomialUn tas binomial est en fait un ensemble d'arbres binomiaux (à comparer avec un tas binaire, qui correspond à un unique arbre binaire). Un arbre binomial est défini récursivement comme suit :
Un arbre binomial d'ordre k peut aussi être construit à partir de deux arbres d'ordre k-1 en faisant de l'un des deux le fils le plus à gauche de la racine de l'autre. Un arbre binomial d'ordre k possède 2k nœuds, et a pour hauteur k. Des variantes d'arbres binomiaux sont aussi utilisées pour construire les tas de Fibonacci. Structure des tas binomiauxUn tas binomial est implémenté en tant qu'ensemble d'arbres binomiaux satisfaisant aux propriétés des tas binomiaux :
La première propriété indique que la racine de chaque arbre binomial possède la plus petite clé de l'arbre. La seconde propriété implique qu'un tas binomial contenant n éléments consiste en au plus ln n + 1 arbres binomiaux. En fait, le nombre et les ordres de ces arbres est déterminé de manière unique par le nombre n d'éléments : chaque tas binomial correspond au bit 1 dans l'écriture binaire du nombre n. Par exemple, 13 correspond à 1101 en binaire, , et donc le tas binomial à 13 éléments consistera en 3 arbres binomiaux d'ordres respectifs 3, 2 et 0 (cf. figure ci-dessous) Les racines des arbres binomiaux sont stockées dans une liste indexée par l'ordre des arbres. 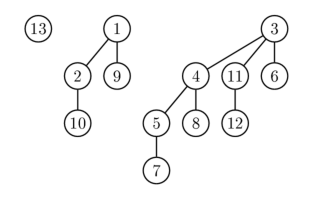 Exemple de tas binomial contenant des éléments de clés 1, 2, ..., 13. Le tas consiste en 3 arbres binomiaux d'ordre 0, 2, et 3. Implémentation des opérationsL'opération de fusion de deux tas est sans doute la plus intéressante et est réutilisée dans la plupart des autres opérations. Les listes de racines des deux tas sont parcourues simultanément, de même que pour le tri fusion. Si seul un des deux tas contient un arbre d'ordre j, celui-ci est ajouté au tas fusionné. Si les deux tas contiennent un arbre d'ordre j, les deux arbres sont fusionnés en un arbre d'ordre j+1 en respectant la structure de tas (la plus grande des deux racines devient fille de la plus petite). Noter que l'on peut avoir besoin de fusionner cet arbre avec un arbre d'ordre j+1 présent dans un des deux tas initiaux. Durant l'algorithme, on examine au plus 3 arbres de chaque ordre (deux provenant des deux tas fusionnés et un formé à partir de deux arbres plus petits). Or l'ordre maximal d'un arbre est ln n et donc la complexité de la fusion est en O(ln n). Pour insérer un nouvel élément dans un tas on crée simplement un nouveau tas contenant uniquement cet élément qu'on fusionne ensuite avec le tas initial, et ce en O(ln n). Pour trouver le plus petit élément du tas, il suffit de trouver le minimum parmi les racines des arbres binomiaux (au nombre maximal de ln n), ce qui se fait une fois de plus en O(ln n). Pour supprimer le plus petit élément du tas, on trouve tout d'abord cet élément pour l'enlever de son arbre binomial. On obtient alors une liste de ses sous-arbres, que l'on transforme en un autre tas binomial, ensuite fusionné au tas précédent. Quand on diminue la clé d'un élément, elle peut devenir plus petite que celle de son père, violant l'ordre en tas de l'arbre. Dans ce cas, on échange l'élément avec son père, voire avec son grand-père, et ainsi de suite jusqu'à ce que l'arbre soit de nouveau ordonné en tas. Chaque arbre binomial ayant pour hauteur maximale ln n, l'opération est en O(ln n). Enfin pour supprimer un élément, on lui diminue sa clé à moins l'infini (plus petite que toutes les autres clés...) puis on supprime le plus petit élément du tas, c’est-à-dire lui-même. Références
Lien externe |
Portal di Ensiklopedia Dunia
