Rotation stellaire

Cette illustration montre le renflement équatorial de l'étoile Achernar causé par sa rotation rapide.

La rotation stellaire désigne la rotation d’une étoile autour de son axe. La vitesse de rotation peut être mesurée par le spectre de l’étoile ou en chronométrant différentes caractéristiques visibles à sa surface.

Puisque les étoiles ne sont pas des corps solides, elles sont sujettes à la rotation différentielle. Ainsi, l’équateur de l’étoile peut tourner avec une vitesse angulaire différente de celle des plus hautes latitudes, ce qui peut produire un renflement équatorial (en) par effet centrifuge. À partir d'une certaine vitesse de rotation, appelée « vitesse de destruction », l'effet centrifuge à l’équateur est égal à la force gravitationnelle[1]. Pour que l'étoile soit stable, la vitesse de rotation doit être inférieure à cette vitesse[1].

Les différences de vitesse angulaire des parties d’une étoile peuvent également avoir un rôle significatif dans la génération d’un champ magnétique[2]. Ce dernier interagit avec le vent stellaire et amène l'étoile à transférer son moment angulaire, ce qui mène graduellement au ralentissement de sa rotation.

La rotation stellaire est un élément fondamental de la gyrochronologie, qui est la détermination de l'âge d'une étoile en fonction de sa rotation[3]. Elle occasionne également un obscurcissement à l’équateur, qui est décrit par le théorème de von Zeipel.

Caractéristiques physiques

Renflement équatorial

La gravité tend à former les objets célestes en une sphère parfaite où la masse est répartie le plus près possible du centre. Toutefois, une étoile en rotation n’est pas de forme sphérique, elle possède un renflement équatorial.

La rotation stellaire de Régulus A est très rapide.

Un exemple extrême de renflement équatorial peut être retrouvé sur l’étoile Régulus A. La vitesse de rotation à l’équateur de cette étoile est de 317 ± 3 km/s, soit une période de rotation de 15,9 heures. Cette vitesse correspond à 86 % de la vitesse de destruction^[C'est-à-dire ?] et amène le rayon équatorial de cette étoile à dépasser le rayon polaire de 32 %[4]. D’autres exemples d’étoiles possédant une grande vitesse de rotation sont Alpha Arae, Pléioné, Véga et Achernar.

Rotation différentielle

La rotation différentielle est observée sur des corps en rotation où la vitesse angulaire varie selon la latitude du point considéré. Normalement, la vitesse angulaire diminue avec l'augmentation de la latitude. Cependant, certains cas inverses ont été observés, comme sur l'étoile HD 31993[5],[6].

Le mécanisme sous-jacent qui cause la rotation différentielle est le mouvement de convection en action à l'intérieur de l'étoile. Il transporte de l'énergie vers la surface à travers le mouvement du plasma. Ce dernier possède une certaine portion de la vitesse angulaire de l'étoile. Lorsque la turbulence est induite par les mécanismes de rotation et de cisaillement, le moment angulaire peut se redistribuer à différentes latitudes à travers le flux méridional[7],[8].

Les interfaces entre les régions ayant des différences de rotation marquées sont considérées comme étant des sites efficaces pour générer l'effet dynamo qui est à l'origine du champ magnétique stellaire. Il y a aussi une interaction complexe entre la distribution de la rotation d'une étoile et son champ magnétique, alors qu'on observe une conversion de l'énergie magnétique en énergie cinétique, ce qui a pour effet de modifier la distribution de la vitesse[2].

La première étoile autre que le Soleil dont la rotation différentielle a été cartographiée en détail est AB Doradus[2],[9].

Obscurcissement à l'équateur

La rotation stellaire occasionne également un obscurcissement à l’équateur, qui est décrit par le théorème de von Zeipel.

Formation

Les étoiles sont le résultat de l'effondrement d'un nuage moléculaire. Lorsque le nuage s'effondre, la conservation du moment angulaire conduit à une augmentation de la rotation des composantes du nuage et entraîne la matière dans la formation d'un disque protoplanétaire. Au centre dense du disque, une proto-étoile se forme et gagne de la chaleur provenant de l'énergie gravitationnelle de l'effondrement. Puisque l'effondrement continue, la vitesse de rotation peut augmenter au point où la proto-étoile en accrétion peut se briser en raison de la trop grande force centrifuge exercée à l'équateur.

Pour que l'étoile se forme, il faut que la vitesse de rotation soit ralentie. Ce ralentissement pourrait être causé par l'interaction qui survient entre le champ magnétique de la proto-étoile et le vent stellaire dans une sorte de freinage magnétique. Le vent stellaire, gagnant en intensité, distribue le moment angulaire et ralentit la vitesse de rotation de la proto-étoile en train de s'effondrer.

Une fois ralenti, le disque protoplanétaire devient de plus en plus sphérique en son centre. Cependant, sa contraction n'aboutit pas à une sphère parfaite : aux pôles, la gravité augmente la contraction, mais à l’équateur son effet est contrecarré par l'effet centrifuge. La forme finale de l’étoile est en équilibre, c’est-à-dire que l’effet de la gravité ne peut réduire davantage le diamètre à l'équateur pour obtenir une forme plus sphérique.

Séquence principale

Vitesse moyenne de rotation selon certains types spectraux[10].

	M☉	R☉	v (${\displaystyle km/s}$)
O5	39,5	17,2	190
B0	17	7,6	200
B5	7,0	4,0	210
A0	3,6	2,6	190
A5	2,2	1,7	160
F0	1,75	1,3	95
F5	1,4	1,2	25
G0	1,05	1.04	12

La plupart des étoiles de la séquence principale qui tournent rapidement sont d'un type spectral situé entre O5 et F5[4],[11]. Pour les étoiles de ces types, les vitesses de rotation augmentent avec la masse pour atteindre un pic chez les jeunes étoiles massives de type B.

Pour les étoiles de la séquence principale, la baisse de la vitesse de rotation peut être déduite par une relation mathématique :

${\displaystyle \Omega _{e}\propto t^{-{\frac {1}{2}}}}$, où ${\displaystyle \Omega _{e}}$ est la vitesse angulaire à l'équateur et t est l'âge de l'étoile[12].

Cette relation est connue sous le nom de loi de Skumanich, découverte par Andrew P. Skumanich en 1972[13].

Les étoiles perdent lentement de la masse par l'émission du vent stellaire via la photosphère. Le champ magnétique des étoiles exerce un certain moment de force sur la matière éjectée, ce qui lui transfère une partie du moment angulaire de l'étoile. Avec le temps, les étoiles se rapprochent graduellement d'une rotation nulle, sans toutefois l'atteindre[14].

Système binaire rapproché

Un système binaire rapproché survient lorsque deux étoiles sont en orbite l’une avec l’autre à une distance moyenne du même ordre de grandeur que leur diamètre. À cette distance, des interactions plus complexes peuvent survenir, comme des effets de marée, des transferts de matière et même des collisions. Les interactions de marées dans un système binaire rapproché peuvent aboutir à une modification des paramètres orbitaux et rotationnels. Le moment angulaire total du système est conservé, mais il peut être transféré entre les périodes orbitales et les vitesses de rotation[15].

Chaque membre d’un système binaire rapproché crée des marées sur l’étoile voisine à travers des interactions gravitationnelles. Cependant, les renflements peuvent être légèrement désalignés par rapport à la direction de l’attraction gravitationnelle. De ce fait, la force gravitationnelle produit une composante de moment de force sur le renflement, conduisant à un transfert de moment angulaire. Ceci implique que le système est en constante évolution, même s'il peut tendre vers un certain équilibre. L’effet peut être plus complexe dans le cas où l’axe de rotation n’est pas perpendiculaire au plan de l’orbite[15].

Pour les systèmes binaires où les étoiles sont en contact ou à moitié détachées, le transfert de masse entre les deux corps peut également aboutir à un transfert significatif de moment angulaire. Ainsi, par exemple, un compagnon en accrétion peut accentuer sa vitesse de rotation jusqu’à ce qu’il atteigne la vitesse de rotation critique et commence ainsi à perdre de la masse le long de son équateur[16].

Étoiles dégénérées

Après qu’une étoile a terminé de générer de l’énergie par fusion thermonucléaire, elle évolue en une forme compacte composée de matière dégénérée. Lors de ce processus, la dimension de l’étoile est réduite de manière importante, ce qui peut occasionner une augmentation de sa vitesse angulaire.

Naine blanche

Sirius A et B.

Une naine blanche est une étoile constituée des produits de la réaction de fusion thermonucléaire survenue durant le stade précoce de sa vie et qui a par la suite manqué de masse pour fusionner des éléments plus massifs. Il s’agit d’un corps très dense supporté par un phénomène de mécanique quantique connu sous le nom de pression de dégénérescence, qui évite à l’étoile de s’effondrer davantage sur elle-même. La plupart des naines blanches ont une faible vitesse de rotation, faiblesse en grande partie due au freinage rotationnel ou à la perte de moment angulaire lorsque l’étoile perd son enveloppe externe lors de la formation de la nébuleuse planétaire.

Une naine blanche à rotation lente ne peut excéder la limite de Chandrasekhar de 1,44 masses solaires sans s’effondrer pour former une étoile à neutrons ou exploser en une supernova de type Ia. Une fois qu’une naine blanche atteint cette masse, par accrétion ou par collision, la force gravitationnelle excèderait la pression exercée par les électrons. Si la naine blanche a une rotation rapide, l’effet de la gravité diminue vers sa région équatoriale, ce qui lui permet de dépasser la limite de Chandrasekhar. Une rotation rapide peut survenir lorsqu’on observe une accrétion de masse résultant d’un transfert de moment angulaire.

Étoile à neutrons

Modèle d'un pulsar.

L’étoile à neutrons émet un faisceau de radiations provenant de ses pôles magnétiques. Le faisceau est dispersé le long d’une surface conique entourant l’axe de rotation. L’étoile à neutrons est une forme très dense d’étoile principalement composée de neutrons. La masse d’une étoile à neutrons se situe dans une plage allant de 1,2 à 2,1 masses solaires. À la suite de l’effondrement, une étoile à neutrons nouvellement formée peut avoir une vitesse de rotation très élevée de l’ordre d’une centaine de tours par seconde.

Les pulsars sont des étoiles à neutrons en rotation disposant d’un champ magnétique. Un faisceau étroit de radiations électromagnétiques est projeté par les pôles des pulsars. Si le faisceau est orienté en direction du Système solaire, la pulsation périodique est détectable de la Terre. L’énergie déployée par le champ magnétique ralentit graduellement la vitesse de rotation du pulsar. Ainsi, il peut se dérouler plusieurs secondes entre chaque pulsation chez les pulsars très âgés.

Trou noir

Schéma d'un trou noir de Kerr.

Un trou noir est un objet qui a un champ gravitationnel suffisamment puissant pour empêcher la lumière de lui échapper. Lorsqu’ils sont formés par effondrement d'une masse en rotation, ils conservent le reste du moment angulaire qui n’a pas été dispersé lors de l’éjection de gaz. Cette rotation entraîne avec elle l’espace compris dans un volume ayant la forme d’un sphéroïde aplati appelé « ergosphère ». La masse tombant dans ce volume gagne de l’énergie par ce processus et une partie de cette masse peut alors être éjectée sans être entrainée dans le trou noir. Lorsque la masse est éjectée, le trou noir perd une partie de son moment angulaire par le processus de Penrose.

La vitesse de rotation d’un trou noir a pu être mesurée jusqu’à une vitesse correspondant à 98,7 % celle de la vitesse de la lumière^[réf. souhaitée].

Mesures

Sauf si elle est observée à partir de ses pôles, les sections de la surface d'une étoile possèdent une composante de mouvement qui s’approche ou s’éloigne de l’observateur. Pour la portion de la surface ayant une composante de vitesse radiale dirigée vers l'observateur, la radiation est décalée vers une fréquence plus haute à cause de l’effet Doppler. De même, pour la région qui a une vitesse radiale s’éloignant de l’observateur, la radiation est décalée vers une fréquence plus basse. De plus, le décalage de chaque extrémité du spectre cause un élargissement des raies d’absorption[17]. Cependant, cet élargissement doit être séparé des autres effets qui élargissent le spectre électromagnétique.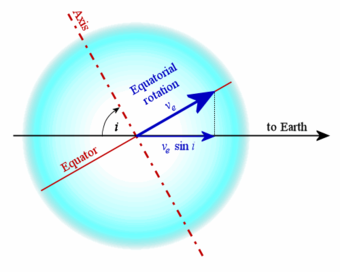

Cette étoile avec une inclinaison ${\displaystyle i}$ prise à partir de la ligne de visée d'un observateur de la Terre et sa vitesse de rotation ${\displaystyle v_{e}}$ à l'équateur.

La composante de la vitesse radiale observée à travers l’élargissement du spectre dépend de l’inclinaison des pôles de l’étoile. La valeur dérivée est donnée par ${\displaystyle v_{e}\cdot \sin i}$, où ${\displaystyle v_{e}}$ est la vitesse rotationnelle à l’équateur et ${\displaystyle i}$ est l’inclinaison. Cependant, ${\displaystyle i}$ n’est pas toujours connue, alors le résultat donne une valeur minimum de la vitesse rotationnelle de l’étoile en question. Si ${\displaystyle i}$ n’est pas un angle droit, la vitesse réelle est plus grande que ${\displaystyle v_{e}\cdot \sin i}$[17], ce terme étant parfois appelé la vitesse rotationnelle projetée.

Pour les étoiles géantes, la microturbulence atmosphérique peut entraîner l’élargissement des raies spectrales, qui est beaucoup plus importante que les effets de la rotation et qui masque le signal. Cependant, une autre approche peut s’employer en utilisant des événements de microlentilles gravitationnelles. Elles se produisent lorsqu’un objet massif passe en avant d’une étoile et amplifie brièvement l’image. Les informations recueillies qui sont plus détaillées permettent de distinguer les effets de microturbulences de ceux de la rotation[18].

Si une étoile affiche une activité magnétique à sa surface par des taches stellaires, elles peuvent permettre d'estimer le taux de rotation. Cependant, certaines caractéristiques peuvent se former à d'autres endroits qu'à l'équateur et migrer à travers les latitudes pendant leur durée de vie. En ce cas, la rotation différentielle peut donner des valeurs variables de la vitesse de rotation. L'activité magnétique stellaire est souvent associée avec une rotation rapide, donc la technique peut être utilisée pour la mesure de ces étoiles[19]. L'observation de taches stellaires a montré que ces caractéristiques peuvent faire varier la vitesse de rotation d'une étoile, comme le champ magnétique a pour effet de modifier la circulation des gaz sur les étoiles[20].

Application

La rotation stellaire est un élément fondamental de la gyrochronologie, qui est la détermination de l'âge d'une étoile en fonction de sa rotation[3].

Notes et références

Notes

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Stellar rotation » (voir la liste des auteurs).

1. (en) J. Hardorp, P. A. Strittmatter « Rotation and Evolution of be Stars » (September 8–11, 1969) (Bibcode 1970stro.coll...48H)
   — « (ibid.) », dans Proceedings of IAU Colloq. 4, Ohio State University, Columbus, Ohio, p. 48
2. (en) Jean-François Donati, « Differential rotation of stars other than the Sun », Laboratoire d’Astrophysique de Toulouse, 5 novembre 2003 (consulté le 24 juin 2007).
3. (en) Sydney A. Barnes, « Ages for illustrative field stars using gyrochronology: viability, limitations and errors », The Astrophysical Journal, vol. 669, n^o 2,‎ 2007, p. 1167–1189 (DOI 10.1086/519295, Bibcode 2007ApJ...669.1167B, arXiv 0704.3068).
4. (en) H. A. McAlister, T. A. ten Brummelaar et al., « First Results from the CHARA Array. I. An Interferometric and Spectroscopic Study of the Fast Rotator Alpha Leonis (Regulus). », The Astrophysical Journal, vol. 628, n^o 1,‎ 2005, p. 439–452 (DOI 10.1086/430730, Bibcode 2005ApJ...628..439M, arXiv astro-ph/0501261).
5. (en) Kitchatinov, L. L.; Rüdiger, G., « Anti-solar differential rotation », Astronomische Nachrichten, vol. 325, n^o 6,‎ 2004, p. 496–500 (DOI 10.1002/asna.200410297, Bibcode 2004AN....325..496K, arXiv astro-ph/0504173).
6. (en) Ruediger, G.; von Rekowski, B.; Donahue, R. A.; Baliunas, S. L., « Differential Rotation and Meridional Flow for Fast-rotating Solar-Type Stars », Astrophysical Journal, vol. 494, n^o 2,‎ 1998, p. 691–699 (DOI 10.1086/305216, Bibcode 1998ApJ...494..691R).
7. (en) Holly Korab, « NCSA Access: 3D Star Simulation », National Center for Supercomputing Applications, 25 juin 1997 (consulté le 27 juin 2007).
8. (en) Küker, M.; Rüdiger, G., « Differential rotation on the lower main sequence », Astronomische Nachrichten, vol. 326, n^o 3,‎ 2004, p. 265–268 (DOI 10.1002/asna.200410387, Bibcode 2005AN....326..265K, arXiv astro-ph/0504411).
9. (en) J.-F. Donati, Cameron A. Collier, « Differential rotation and magnetic polarity patterns on AB Doradus », Monthly Notices of the Royal Astronomical Society, vol. 291, n^o 1,‎ 1997, p. 1–19 (Bibcode 1997MNRAS.291....1D).
10. (en) D. McNally, « The distribution of angular momentum among main sequence stars », The Observatory, vol. 85,‎ 1965, p. 166–169 (Bibcode 1965Obs....85..166M).
11. (en)Peterson, Deane M. et al. « Resolving the effects of rotation in early type stars » (2004) (Bibcode 2004SPIE.5491...65P)
    — « (ibid.) », dans New Frontiers in Stellar Interferometry, Proceedings of SPIE Volume 5491, Bellingham, Washington, USA, p. 65
12. (en) Jean-Louis Tassoul, Stellar Rotation, Cambridge, MA, Cambridge University Press, 1972, 256 p. (ISBN 0-521-77218-4, lire en ligne).
13. (en) Andrew P. Skumanich, « Time Scales for CA II Emission Decay, Rotational Braking, and Lithium Depletion », The Astrophysical Journal, vol. 171,‎ 1972, p. 565 (DOI 10.1086/151310, Bibcode 1972ApJ...171..565S).
14. (en) Kyoji Nariai, « Mass Loss from Coronae and Its Effect upon Stellar Rotation », Astrophysics and Space Science, vol. 3, n^o 1,‎ 1969, p. 150–159 (DOI 10.1007/BF00649601, Bibcode 1969Ap&SS...3..150N).
15. (en) P. Hut, « Tidal evolution in close binary systems », Astronomy and Astrophysics, vol. 99, n^o 1,‎ 1999, p. 126–140 (Bibcode 1981A&A....99..126H).
16. (en) D. Weaver, M. Nicholson, « One Star's Loss is Another's Gain: Hubble Captures Brief Moment in Life of Lively Duo », NASA Hubble, 4 décembre 1997 (consulté le 3 juillet 2007).
17. (en) Shajn, G.; Struve, O., « On the rotation of the stars », Monthly Notices of the Royal Astronomical Society, vol. 89,‎ 1929, p. 222–239 (Bibcode 1929MNRAS..89..222S)
18. (en) Andrew Gould, « Measuring the Rotation Speed of Giant Stars from Gravitational Microlensing », Astrophysical Journal, vol. 483, n^o 1,‎ 1997, p. 98–102 (DOI 10.1086/304244, Bibcode 1996astro.ph.11057G, arXiv astro-ph/9611057).
19. (en) W. Soon, P. Frick, S. Baliunas, « On the rotation of the stars », The Astrophysical Journal, vol. 510, n^o 2,‎ 1999, L135–L138 (DOI 10.1086/311805, Bibcode 1999ApJ...510L.135S, arXiv astro-ph/9811114).
20. (en) Cameron A. Collier, J.-F. Donati, « Doin' the twist: secular changes in the surface differential rotation on AB Doradus », Monthly Notices of the Royal Astronomical Society, vol. 329, n^o 1,‎ 2002, L23–L27 (DOI 10.1046/j.1365-8711.2002.05147.x, Bibcode 2002MNRAS.329L..23C, arXiv astro-ph/0111235).

Voir aussi

Articles connexes

• Cassure de Kraft
• Champ magnétique stellaire
• Freinage magnétique (astronomie)