|
Vitesse radiale La vitesse radiale est la vitesse d'un objet mesurée dans la direction du rayon (ou la ligne de visée) vers (valeur négative) ou depuis (valeur positive) le point d'observation. La mesure de la vitesse radiale se fait de plusieurs façons et ce concept est utilisé dans de nombreux domaines dont la mesure par radar Doppler, les sonars, les échographies et en astronomie. PrincipeLe mouvement d'un objet par rapport à un observateur peut être décomposé en deux axes orthogonaux : radial et tangentiel. La vitesse radiale (vr) (VR(t) sur le graphique) ne donne donc pas la valeur du vecteur vitesse de l'objet (vs) (V(t) sur le graphique), mais uniquement la composante de celui-ci sur la ligne de visée. La vitesse radiale est donc vr = vs cos θ, où θ est l'angle formé par la ligne de visée vers le mobile et la trajectoire de celui-ci. Pour connaître les autres composantes, c'est-à-dire les composantes tangentielles à la ligne de visée verticalement et horizontalement (VT(t) sur le graphique à deux dimensions), il faut en général observer le mouvement propre de l'objet, et connaître sa distance. Ces deux paramètres sont souvent difficiles à déterminer, en particulier le premier. MesureLa vitesse radiale peut être mesurée de plusieurs manières. Dans une situation simple, l'observateur peut noter le temps de passage de la cible près de repères qui sont à des distances connues de sa propre position. Par exemple, un automobiliste sur une autoroute peut estimer la vitesse d'approche d'une automobile arrivant par une bretelle d'accès. Les radars et les sonars émettent des ondes qui sont retournées par des cibles. L'onde revenant d'un objet possédant une vitesse radiale est sujette à l'effet Doppler, par conséquent la fréquence retournée (Ft) diminue (décalage vers le rouge) si l'objet s'éloigne (vitesse radiale positive) et augmente (décalage vers le bleu) s'il se rapproche (vitesse radiale négative). En mesurant cette variation, Fd, le système en tire la vitesse radiale : avec c la vitesse de la lumière pour les ondes électromagnétiques et la vitesse du son pour les ondes sonores. En astronomie, ce sont les objets célestes qui émettent de la lumière. Selon leur composition chimique, cette lumière se décompose en raies à des longueurs d'onde très précises. C'est le décalage de la longueur d'onde d'une raie spectrale qui sera mesuré pour connaître la composante radiale. Avec λ0 comme longueur d'onde de la raie spectrale qui serait mesurée si l'objet était au repos et λm la longueur d'onde mesurée, la vitesse radiale vr s'écrit
où c est la vitesse de la lumière. En pratique cette formule ne vaut que pour les basses vitesses, c'est-à-dire les vitesse significativement inférieures à la vitesse de la lumière. ApplicationsAstronomie La vitesse radiale d'une étoile ou d'un autre objet lumineux éloigné peut être mesurée précisément par spectrovélocimétrie en prenant un spectre à haute-résolution et en comparant les longueurs d'onde mesurées de raies spectrales connues aux longueurs d'onde de ces mêmes raies mesurées en laboratoire. Par convention, une vitesse radiale positive indique que l'objet s'éloigne (on parle de décalage vers le rouge/rougissement) et une vitesse négative que l'objet se rapproche (décalage vers le bleu/bleuissement). La composante tangentielle du mouvement est souvent inconnue, le mouvement propre pour des objets situés hors de notre Galaxie étant difficile à mesurer[1]. Pour les pulsars, il est également possible de déterminer leur vitesse orthogonale en mesurant très précisément leur accélération radiale. Cette méthode repose sur un phénomène physique très simple appelé l'effet Shklovski. Cependant, dans le cas des pulsars, c'est la vitesse radiale qui est difficile à déterminer. La notion de vitesse radiale en cosmologie, où l'expansion de l'Univers ne doit pas être vue en termes de déplacement d'objets dans l'espace mais en termes d'une dilatation de l'espace lui-même, a donc un sens différent. Étoiles binairesPour beaucoup d'étoiles binaires, le mouvement orbital entraîne souvent des variations de vitesse radiale de plusieurs kilomètres par seconde. Comme le spectre de ces étoiles varie à cause de l'effet Doppler, elles sont appelées binaires spectroscopiques. Les études de vitesse radiale peuvent être utilisées pour contraindre les masses des étoiles ainsi que certains éléments orbitaux, tels que l'excentricité, voire le demi-grand axe si les masses sont déterminées par ailleurs. La même méthode est aussi utilisée pour détecter des planètes autour d'étoiles. En pratique, connaissant la vitesse radiale et la période orbitale du système, on déduit une quantité appelée fonction de masse, dépendant de la masse des deux objets et de l'inclinaison du plan orbital du système. Dans les cas où certaines de ces quantités peuvent être déduites (par exemple dans une binaire X, une des deux masses est en général très proches de la masse de Chandrasekhar si l'objet compact du système est une étoile à neutrons ; l'inclinaison peut être estimée si l'on observe le phénomène d'éclipses — on parle alors de binaire à éclipses). ExoplanètesLa mesure des vitesses radiales est une des méthodes utilisées actuellement pour détecter des exoplanètes autour d'une étoile, de façon identique à ce qui se fait pour les étoiles doubles (cf. paragraphe précédent). Bien que la masse de la planète soit petite comparée à la masse de l'étoile autour de laquelle elle tourne, elle produit un mouvement faible mais mesurable de l'étoile qui se traduit par une variation de la vitesse radiale de l'étoile[2]. Ce mouvement peut par la suite être transcrit à l'aide de la fonction de masse comme une mesure d'une certaine combinaison de la masse des deux objets et de l'inclinaison de son plan orbital. Si le spectre de l'étoile est suffisamment bien mesuré, on peut à partir de son type spectral et de sa distance (si elle est connue) estimer sa masse. Connaissant la masse de l'étoile, on déduit alors la quantité Mp sin i, où Mp est la masse de la planète et sin i le sinus de l'inclinaison du système. Cela donne une estimation (en réalité une limite inférieure) à la masse de la planète. Radar et sonar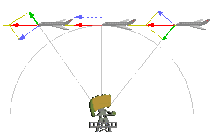 Les radars et les sonars servent à la détection de cibles comme les avions, les précipitations ou les navires. Cependant, ils ne peuvent noter que la vitesse radiale de celles-ci grâce au décalage Doppler induit par son rapprochement ou son éloignement. Ainsi sur l'image de droite, un radar suivant un avion se déplaçant parallèlement au sol ne peut noter que sa vitesse radiale (flèche verte) et non sa vitesse réelle (flèche rouge). Il est par contre possible de déduire avec une certaine précision la vraie vitesse et direction si la vitesse radiale de la cible est prise à intervalles réguliers. En effet, la composante radiale variant comme le cosinus de l'angle de visée entre le radar et la cible, il est possible d'extraire par analyse numérique l'information sur la vitesse réelle. La connaissance de la vitesse radiale permet ainsi d'estimer le type de cible et son temps de passage, de filtrer les cibles fixes n'ayant pas de vitesse radiale, etc. Voir aussiRéférences
|

