|
Plan projectif (structure d'incidence)La géométrie projective peut être introduite de deux façons : par les espaces vectoriels sur un corps donné, ou directement en axiomatisant une relation dite d'incidence entre points et droites (la relation d'appartenance d'un point à une droite). Alors que pour les espaces de dimension au moins 3 ces approches s'avèrent équivalentes, dans le cas du plan, ce n'est pas le cas : le plan projectif défini comme structure d'incidence n'est pas nécessairement le plan projectif défini sur un corps, ceci parce que le théorème de Desargues ne se démontre avec les axiomes d'incidence qu'à partir de la dimension 3. Le phénomène est le même en géométrie affine et les plans projectifs, définis comme structure d'incidence, sont liés de façon étroite aux plans affines qui peuvent aussi se définir comme une structure d'incidence. L'axiomatisation ici introduite est donc très générale, en particulier un plan projectif peut être ou non fini, et certains plans projectifs finis satisfaisant ces axiomes ne sont pas des plans définis sur un corps fini. Axiomes d'incidence de la géométrie projective planeUne structure d'incidence Σ = (Π, Δ, Φ) est constituée de deux ensembles d'objets primitifs, un ensemble de points Π et un ensemble de droites Δ, et d'une relation Φ dite d'incidence entre points et droites (c'est-à-dire que Φ est une partie de Π × Δ). La relation d'incidence s'exprime usuellement de plusieurs façons. Le point A est incident à la droite d se dit également d passe par A, A est sur d. Trois points ou plus qui sont sur une même droite sont dits alignés (sur cette droite). Trois droites ou plus qui passent par un même point sont dites concourantes (en ce point). Deux droites distinctes se coupent en un point si celui-ci est sur les deux droites. AxiomesUn plan projectif est une structure d'incidence satisfaisant les axiomes suivants[1],[2]
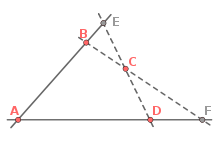 Quadrangle completUne variante[4] est de remplacer les deux derniers axiomes par l'axiome suivant.
Une telle configuration de 4 points définit donc 6 droites (distinctes). Elle est appelée quadrangle complet. On démontre à partir des axiomes P1 à P4 l'existence d'un quadrangle complet, et même l'énoncé plus général suivant.
En effet soient 3 points A, B, D non alignés qui définissent donc deux droites (AB) et (AD) par (P1), qui sont distinctes. Par P3 il existe alors un troisième point sur (AB), soit E et un troisième point sur (AD), soit F. Les points E et F sont également distincts de D et B (les droites (AB) et (AD) étant distinctes). À nouveau par (P1), on a deux droites (BF) et (DE), qui sont distinctes car les points d'intersection de ces droites avec (AB) sont distincts, et par (P2). Elles définissent donc par (P2) un point C = (BF) ∩ (DE). On vérifie que l'alignement de C avec deux points parmi A, B et D contredit les hypothèses sur A, B, D, E et F, en utilisant (P1) et (P2). Réciproquement, de l'existence de 4 points non alignés on déduit évidemment (P4). Étant donné une droite d, si elle ne passe que par au plus un des 4 points non alignés, les 3 autres points définissent 3 droites distinctes qui intersectent d en 3 points distincts (par (P1) et (P2)). Si d passe par deux des 4 points non alignés, on construit, en renversant la construction précédente du quadrangle un troisième point sur d. On a donc bien (P3). ExemplesLe plan projectif réelUn exemple de structure d'incidence qui satisfait ces quatre axiomes est le plan projectif réel PG(2, R). On prend comme ensemble des points l'ensemble des droites vectorielles de R3 et comme ensemble de droites l'ensemble des plans vectoriels de R3. La relation d'incidence est l'inclusion ensembliste, ou ce qui revient au même celle de sous-espace vectoriel. Les quatre axiomes sont évidemment satisfaits. Le plan projectif réel satisfait bien d'autres propriétés qui ne se déduisent pas des axiomes d'incidence, à commencer par les propriétés de Desargues et de Pappus.  Le plan de FanoLa construction précédente peut être reproduite sur n'importe quel corps (commutatif ou non). L'exemple le plus simple est celui du corps à deux éléments F2. On obtient un plan de 7 points et 7 droites, le plan de Fano PG(2, F2). Il s'avère être le seul plan à 7 points à isomorphisme de structure d'incidence près, et peut être construit directement comme le plus petit plan satisfaisant les axiomes d'incidence. Le plan de MoultonLes deux exemples précédents, comme tous les plans projectifs PG(2, K) construits sur un corps K, satisfont la propriété de Desargues (trivialement dans le cas du plan de Fano, puisqu’il n’y existe pas de triangles n’ayant aucun sommet commun). David Hilbert a montré en 1899 dans ses Grundlagen der Geometrie (Les fondements de la géométrie) l'existence d'un plan affine ne satisfaisant pas cette propriété, et Moulton a donné un exemple plus simple en 1902 (repris ensuite par Hilbert). Le plan de Moulton est un plan affine, mais peut être prolongé en un plan projectif par la construction usuelle. Ce plan satisfait les axiomes d'incidence, mais pas la propriété de Desargues. Plan projectif et plan affineIl existe un lien étroit entre plan projectif et plan affine : historiquement le plan projectif peut être vu comme un plan affine complété par des points sur une droite à l'infini. Ceci est valide pour les axiomatisations par axiomes d'incidence[5]. On passe du plan projectif au plan affine en enlevant une droite quelconque, de même que les points sur cette droite. Étant donné une structure d'incidence (Π, Δ, Φ) et une droite δ de Δ, appelons Π - δ l'ensemble des points de la structure qui ne sont pas sur δ, alors :
En particulier les droites qui s'intersectaient en δ dans le plan projectif deviennent parallèles dans le plan affine obtenu en enlevant δ (dite dans ce contexte droite à l'infini). La vérification des axiomes est immédiate. Réciproquement, étant donné une structure d'incidence qui satisfait les axiomes d'incidence de plan affine, on obtient une structure d'incidence qui satisfait les axiomes d'incidence de plan projectif en ajoutant une droite dite droite à l'infini, et pour chaque direction de droites (ensemble de toutes les droites parallèles à une droite donnée) un point dit point à l'infini de cette direction. La relation d'incidence est étendue de façon que :
Là encore on vérifie facilement que la structure d'incidence obtenue satisfait les axiomes de plan projectif. PerspectivesOn appelle points d'une droite d les points qui sont incidents à d (c'est-à-dire sur d). Un point qui n'est pas sur d est dit extérieur à d. Une conséquence immédiate des axiomes est que, étant donné un point A extérieur à une droite d, il existe une bijection entre les droites passant par A et les points de d. Cette bijection associe à un point M de d l'unique droite passant par A et M (selon (P1) car A extérieur à d). Réciproquement une droite δ passant par A coupe d en un unique point M (selon (P2), car les droites δ et d sont distinctes, A étant sur δ et pas sur d). L'axiome (P4) assure qu'étant donné un point, il existe une droite qui ne passe pas par ce point. Par l'axiome (P3) et la propriété ci-dessus, on a :
Étant donnés deux droites δ et d et un point extérieur à ces deux droites, soit S, l'application qui a un point M de d associe l'unique point d'intersection de δ et (SM) est une bijection (comme composée d'une bijection telle que définie ci-dessus pour d et de sa réciproque pour δ). Elle est appelée perspective ou projection de centre S de d sur δ[6] De la même façon, étant donnés deux points A et B distincts, une droite d ne passant par aucun de ces deux points définit une bijection entre l'ensemble des droites passant par A et l'ensemble des droites passant par B. Au paragraphe précédent, par la construction du quadrangle, on a montré qu'étant donnés deux droites distinctes, il existe un point qui n'est sur aucune de ces deux droites, et donc une perspective (qui est une bijection) de centre ce point entre les deux droites. Par la même construction du quadrangle, on montre qu'étant donné deux points distincts A et B, il existe une droite qui ne passe pas par ces deux points et donc une bijection entre l'ensemble des droites passant par A et l'ensemble des droites passant par B. Par composition à nouveau, on a aussi une bijection entre l'ensemble des points d'une droite et l'ensemble des droites passant par un point en toute généralité (même si le point est sur la droite). Dualité Une propriété particulière à la géométrie projective est la symétrie de la relation d'incidence, c'est ce que l'on appelle la dualité. Un énoncé dual d'un autre énoncé s'obtient en échangeant les rôles des points et des droites : le point A est sur la droite d devient la droite a passe par le point D. Une configuration est un ensemble de points et de droites liés par certaines relations exprimées en termes d'incidence, par exemple un triangle est constitué de 3 points non alignés, et la configuration duale est constituée de 3 droites non concourantes. Voici quelques exemples de dualité, pour des configurations ou des énoncés :
Les énoncés duaux des 4 axiomes sont les suivants.
On s'aperçoit immédiatement que la dualité échange les deux premiers axiomes. Le dual du troisième axiome a été démontré précédemment. Par (P4), il existe 3 points non alignés A, B et C, et les droites (AB), (AC) et (BC) ne peuvent être concourantes, car si elles l'étaient, ce serait en un point distinct de A, B et C, ces trois points étant distincts 2 à 2, et les 3 droites seraient confondues ce qui est exclu. Les énoncés duaux des 4 axiomes sont donc démontrables, et si un énoncé se déduit de axiomes (P1), (P2), (P3) et (P4), son énoncé dual se déduit exactement de la même façon des énoncés duaux (P1*), (P2*), (P3*) et (P4*), donc des axiomes[7]. Cette propriété particulière à la géométrie projective (points et hyperplans dans le cas général) est le principe de dualité. Elle est fausse en géométrie affine plane, où l'axiome (P1) est satisfait, mais pas son dual (P1*) = (P2). L'ajout de nouveaux axiomes (Desargues, Pappus) conservera la dualité. Étant donné une structure d'incidence, Σ = (Π, Δ, Φ), la structure duale est Σ* = (Δ, Π, Φ*) où Φ* est la relation symétrique de Φ. Si Σ est un plan projectif, Σ* également : c'est une autre façon d'exprimer le principe de dualité ; Σ* est appelé plan projectif dual de Σ. Une configuration peut être identique à sa configuration duale, par exemple un triangle vu comme 3 sommets et 3 côtés, la dualité échange sommets et côtés. On l'appelle autoduale. La configuration du plan de Fano : 7 points sur 7 droites, chaque droite passant chacune par 3 points, et chaque point étant sur 3 droites, est autoduale : non seulement le dual du plan de Fano est un plan projectif mais il lui est isomorphe (les couleurs du dessin ci-dessus indiquent l'isomorphisme). C'est le cas de tout plan projectif défini sur un corps. La configuration de Desargues (10 points et 10 droites) est également autoduale, et la propriété duale de celle de Desargues est sa réciproque. Autres axiomesIl est possible de déterminer plus précisément les géométries projectives planes en ajoutant des axiomes exprimés dans le langage de l'incidence. Plans projectifs arguésiensUn plan projectif arguésien (ou desarguésien, ou de Desargues) satisfait, en plus des axiomes d'incidence, l'axiome de Desargues, l'énoncé du théorème pris comme axiome. Les plans projectifs arguésiens sont exactement les espaces projectifs PG(2, K) de dimension 2 sur un corps K qui peut être un corps gauche[8]. En dimension supérieure ou égale à 3, la propriété de Desargues est un théorème, et donc un plan projectif est un plan d'un espace projectif de dimension supérieure ou égale à 3 si et seulement s'il satisfait l'axiome de Desargues. Axiome de Desargues. — Si les deux triangles (non plats) ABC et A'B'C' ont leurs sommets sur 3 droites distinctes (AA') , (BB') et (CC') et concourantes alors les points P = (BC) ∩ (B'C'), Q = (AC) ∩ (A'C') et R = (AB) ∩ (A'B') sont alignés. Parmi ces plans PG(2, K), on distingue les plans projectifs de Pappus, qui satisfont l'axiome de Pappus (lequel a pour conséquence la propriété de Desargues, voir le théorème de Hessenberg). Ce sont ceux pour lesquels le corps K est commutatif[9]. Axiome de Pappus. — Si (A,B,C) et (A',B',C') sont deux triplets de points alignés distincts, alors les points P = (BC') ∩ (B'C), Q = (AC') ∩ (A'C) et R = (AB') ∩ (A'B) sont alignés. Il est également possible de prendre pour axiome supplémentaire l'axiome de Fano, le fait de ne pas contenir de configuration de Fano, ce qui revient à imposer au corps K d'avoir une caractéristique différente de 2 (voir l'article plan de Fano). Axiome de Fano. — Un quadrilatère complet a ses 3 points diagonaux non alignés. Plans projectifs non arguésiensUne particularité de la dimension 2 est que l'axiome de Desargues n'est pas nécessairement vérifié. Il est possible, par exemple, de s'intéresser à des plans ne vérifiant que certains cas particuliers de l'axiome de Desargues. Plans projectifs finisPour tout plan projectif fini, il existe un entier n ≥ 2, appelé son ordre, tel que chaque droite passe par exactement n + 1 points et chaque point appartient à exactement n + 1 droites (voir paragraphe Perspectives). Tout plan projectif fini d'ordre n est donc un système de Steiner S(2, n + 1, v) — c'est-à-dire constitué de v points et b droites à n + 1 points, 2 points distincts passant par une droite et une seule — dans lequel, de plus, le nombre de droites incidentes à chaque point est égal à n + 1, ce qui équivaut à b = v, ou encore, à v – 1 = n(n + 1). Un plan projectif fini d'ordre n a donc n2 + n + 1 points et autant de droites. On peut le retrouver plus géométriquement : en distinguant un point S, tout autre point est sur une droite passant par S par l'axiome (P1), on a vu qu'il y avait n + 1 droites distinctes passant par S, et sur chacune d'entre elles n points en plus de S. Ces points sont tous distincts par (P2), d'où 1 + n(n + 1) points. Par dualité, le nombre de droites d'un tel plan est également n2 + n + 1. Réciproquement, tout système de Steiner S(2, n + 1, n2 + n + 1) est un plan projectif fini d'ordre n[10]. Si un plan projectif fini d'ordre n est arguésien, c'est-à-dire de la forme PG(2, K) pour un certain corps K, alors K est le corps fini à n éléments, si bien que le plan vérifie la propriété de Pappus (car tout corps fini est commutatif d'après le théorème de Wedderburn) et que n est une puissance d'un nombre premier. Les plus petits plans projectifs non arguésiens sont d'ordre 9 (= 32). Il en existe 3, dont deux sont duaux l'un de l'autre (et le troisième auto-dual) [11]. Tous les plans projectifs finis connus ont pour ordre une puissance de nombre premier. Notes et références
Ouvrages cités
Voir aussiBibliographie
Articles connexes |
