Grammaire régulière

En informatique théorique, en théorie des langages, une grammaire régulière, rationnelle ou à états finis est une grammaire hors-contexte particulière qui décrit un langage régulier. Les grammaires régulières donnent donc une autre possibilité que les expressions rationnelles et les automates finis pour décrire un langage régulier.

Définition

Une grammaire régulière peut être « à gauche » ou « à droite ».

• Une grammaire régulière à gauche est un ensemble de règles de la forme :

${\displaystyle X\rightarrow Ya}$

${\displaystyle X\rightarrow a}$

${\displaystyle X\rightarrow \epsilon }$

où ${\displaystyle X}$, ${\displaystyle Y}$ sont des symboles non-terminaux et ${\displaystyle a}$ un symbole terminal.

• Une grammaire régulière à droite est un ensemble de règles de la forme :

${\displaystyle X\rightarrow aY}$

${\displaystyle X\rightarrow a}$

${\displaystyle X\rightarrow \epsilon }$

où ${\displaystyle X}$, ${\displaystyle Y}$ sont des symboles non-terminaux et ${\displaystyle a}$ un symbole terminal. De plus, comme pour toutes grammaires, on considère un non-terminal particulier appelé axiome et noté ${\displaystyle S}$.

Exemple

La grammaire suivante est une grammaire régulière à droite :

${\displaystyle S\rightarrow dA\mid rB\mid mC\mid \epsilon }$

${\displaystyle A\rightarrow oS}$

${\displaystyle B\rightarrow eS}$

${\displaystyle C\rightarrow iS}$

Avec la grammaire précédente, on peut engendrer le mot ${\displaystyle dodomi}$. En effet : ${\displaystyle S\rightarrow dA\rightarrow doS\rightarrow dodA\rightarrow dodoS\rightarrow dodomC\rightarrow dodomiS\rightarrow dodomi}$.

Équivalence entre automates finis et grammaires régulières

On peut transformer de manière effective une grammaire régulière à droite en automate fini déterministe et vice versa. Les non-terminaux correspondent aux états de l'automate.

Exemple

Considérons la grammaire ci-dessus. L'automate correspondant est le suivant :

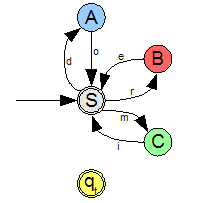
La suite de dérivations ${\displaystyle S\rightarrow dA\rightarrow doS\rightarrow dodA\rightarrow dodoS\rightarrow dodomC\rightarrow dodomiS\rightarrow dodomi}$ correspond à la lecture du mot ${\displaystyle dodomi}$ dans l'automate où on passe successivement dans les états : S, A, S, B, S, C, S.

Définition formelle

Soit une grammaire régulière à droite ${\displaystyle G=\{N,\Sigma ,P,S\}}$, alors l'automate ${\displaystyle A=\{Q,\Sigma ',\delta ,Q_{0},Q_{T}\}}$ équivalent à G est défini tel que:

• ${\displaystyle Q=N\cup \{q_{t}\}}$ avec ${\displaystyle Q}$ l'ensemble des états et ${\displaystyle q_{t}}$ un état puits terminal,
• ${\displaystyle \Sigma '=\Sigma }$ avec ${\displaystyle \Sigma '}$ l'ensemble des symboles terminaux
• ${\displaystyle Q_{0}=S}$ avec ${\displaystyle Q_{0}}$ l'état initial
• ${\displaystyle \delta \in Q\times \Sigma \rightarrow Q}$ est la fonction de transition telle que, à la lecture d'un terminal ${\displaystyle x}$ à partir d'un état ${\displaystyle q_{i}}$ vers un autre état ${\displaystyle q_{f}=\delta (q_{i},x)}$.

La lecture de ${\displaystyle P}$ permet de construire ${\displaystyle \delta }$. Pour chaque ${\displaystyle Pi\in P}$:

• Si ${\displaystyle P_{i}=X\rightarrow aY}$ alors on a ${\displaystyle \delta (X,a)=Y}$
• Si ${\displaystyle P_{i}=X\rightarrow a}$ alors on a ${\displaystyle \delta (X,a)=q_{t}}$
• Si ${\displaystyle P_{i}=X\rightarrow \epsilon }$ alors on a ${\displaystyle X\in Q_{T}}$, ${\displaystyle Q_{T}}$ L'ensemble des états terminaux.

Le même type de jeu de règles peut être établi pour une grammaire régulière à gauche.

Liens externes

• Cours sur les grammaires régulières (avec introduction sur les grammaires en général).