|
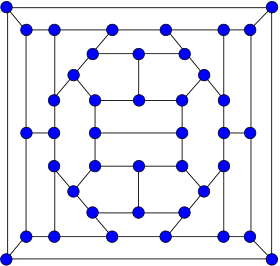
42-graphe de Grinberg
Le 42-graphe de Grinberg est, en théorie des graphes, un graphe 3-régulier possédant 42 sommets et 63 arêtes. PropriétésPropriétés généralesLe diamètre du 42-graphe de Grinberg, l'excentricité maximale de ses sommets, est 7, son rayon, l'excentricité minimale de ses sommets, est 6 et sa maille, la longueur de son plus court cycle, est 4. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes. Le 42-graphe de Grinberg peut être construit à partir du 44-graphe de Grinberg en supprimant une certaine arête ainsi que ses deux extrémités[1]. ColorationLe nombre chromatique du 42-graphe de Grinberg est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe. L'indice chromatique du 42-graphe de Grinberg est 3. Il existe donc une 3-coloration des arêtes du graphe telles que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal. Propriétés algébriquesLe groupe d'automorphismes du 42-graphe de Grinberg est un groupe abélien d'ordre 4 isomorphe à Z/2Z×Z/2Z, le groupe de Klein. Le polynôme caractéristique de la matrice d'adjacence du 42-graphe de Grinberg est : . Voir aussiLiens internesLiens externesRéférences
|
||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia