Árbol radial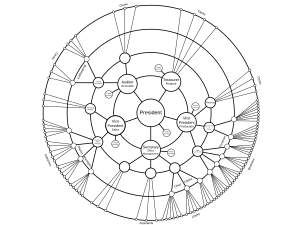

Ejemplo de un árbol radial, tomado de una gráfica de 1924 que enfatiza la autoridad central[1]​

Un árbol radial o mapa circular es una representación visual de una topología arbórea (por ejemplo, un árbol) de manera que crezca hacia afuera, radialmente. Es una de las muchas maneras existentes para visualizar un árbol,[2]​[3]​ con ejemplos que datan de inicios del siglo XX.[4]​ Es un tipo de infografía.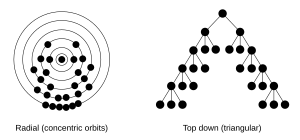

Árbol radial y árbol triangular

Comparación con otras representaciones

En un árbol tradicional el primer nodo está hasta arriba y el resto de los nodos abajo, generalmente cada uno de estos nodos tiene otros hijos, por lo que el árbol resultante tendrá una estructura triangular, parecida a un pino. En contraste, en la representación radial, el nodo raíz se encuentra en el centro de un círculo y cada nivel del árbol es representado por una órbita alrededor de este nodo, el nivel más profundo será el perímetro del círculo.

La distancia entre cada órbita es proporcional al radio del círculo, a mayor radio la circunferencia será mayor y habrá más espacio para los nodos, una situación ideal para el crecimiento hacia abajo de los árboles. En el contexto de árboles, los términos nivel y profundidad son intercambiables.[5]​ Una consideración importante es que el número de nodos en un nivel aumenta de modo exponencial (suponiendo que cada nodo puede tener tantos nodos como el nodo raíz) y la circunferencia es una función lineal, por lo que en cada órbita sucesiva los nodos estarán cada vez más apretados.

Estructura básica de la representación

Estructura de un árbol radial

La distancia «d» es la distancia entre los niveles de la gráfica, se debe de elegir de modo que la imagen quepa en la pantalla. Generalmente se empieza a trabajar del centro hacia afuera. En el primer nivel todos los nodos tienen el mismo padre (el nodo raíz) y, dependiendo del número de hijos que tengan, pueden ser distribuidos equitativamente en la circunferencia o distribuirse de manera proporcional al número de hijos, en los niveles superiores la distribución de los hijos se lleva a cabo en el segmento de la circunferencia asignado a los padres, evitando que dos nodos ocupen la misma posición.

Existen variaciones de este algoritmo que se ajustan a las características de los árboles, por ejemplo, permiten crear representaciones balanceadas, permiten que el usuario cambie el nodo central, en el caso de visualizaciones interactivas[6]​ o acomodar los títulos de los nodos y mezclar representaciones basadas en algoritmos de fuerzas y representaciones radiales.[7]​

Esta representación tiene algunas similitudes con un árbol hiperbólico, siendo la principal diferencia que estos se basan en geometría hiperbólica y los árboles radiales usan una distancia entre órbitas lineal.

Ejemplos

  • MindManager and MindMapper son programas para crear mapas mentales y pueden utilizar representaciones radiales, aunque solamente en dos niveles.
  • SpicyNodes es una metodología de visualización de jerarquías que permite moverse entre nodos.

Referencias

  1. ↑ W. H. Smith., Graphic Statistics in Management (McGraw-Hill Book Company, New York, ed. First, 1924) http://www.visualcomplexity.com/vc/project.cfm?id=10
  2. ↑ Varias visualizaciones en dos dimensiones de grafos y redes, de la documentación de SpicyNodes (en inglés)
  3. ↑ http://www.visualcomplexity.com/vc/project.cfm?id=26
  4. ↑ http://www.visualcomplexity.com/vc/project.cfm?id=289
  5. ↑ Greg Book & Neeta Keshary. "Radial Tree Graph Drawing Algorithm for Representing Large Hierarchies." University of Connecticut December 2001 (en inglés)
  6. ↑ Yee, K.-P, D. Fisher, R. Dhamija, & M. Hearst. “Animated Exploration of Dynamic Graphs with Radial Layout”. Proc. Information Visualization, 43-50, 2001. (en inglés)
  7. ↑ Douma, Michael, Greg Ligierko, Ovidiu Ancuta, P. Gritsai, and S. Liu. SpicyNodes: Radial Layout Authoring for the General Public. InfoVis 2009. Atlantic City, NJ. October 2009. Presentation. (en inglés)

Enlaces externos