|
Trapezoedro disminuido
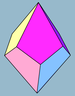
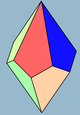
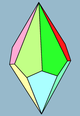
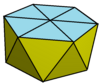
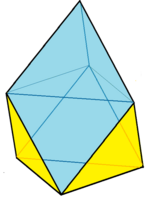
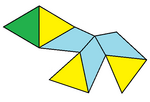
En geometría, un trapezoedro disminuido es un tipo de figura tridimensional que pertenece a un conjunto infinito de poliedros, construidos eliminando uno de los vértices polares de un trapezoedro y reemplazándolo por una nueva cara (en un proceso denominado disminución). Tiene una cara base n-gonal regular, n caras triangulares alrededor de la base y n deltoides con un vértice común en la parte superior. Las caras deltoidales también se pueden sustituir por rombos con proporciones específicas. Junto con el conjunto de pirámides y pirámides elongadas, estas figuras son topológicamente autoduales. También se puede ver como un antiprisma n-gonal aumentado, con una pirámide n-gonal aumentada en una de las caras n-gonales, y cuya altura se ajusta para que las caras superiores triangulares del antiprisma puedan hacerse coplanarias a las caras de la pirámide, para fusionarse en caras con forma de deltoide. También están relacionados con las pirámides giroelongadas, como antiprismas aumentados y que son sólidos de Johnson para n= 4, 5. Esta secuencia de figuras presenta conjuntos de dos triángulos en lugar de caras con forma de deltoide. Ejemplos
Casos especialesHay tres casos geométricos especiales del trapezoedro trigonal disminuido. El más simple es un cubo disminuido. El Chestahedro, que lleva el nombre del artista Frank Chester, está construido con triángulos equiláteros alrededor de la base y la geometría ajustada para que las caras de los deltoides tengan la misma área que los triángulos equiláteros.[1][2] El último puede verse como un sólido aumentado, formado a partir de un tetraedro regular y un octaedro, dejando 10 caras de triángulos equiláteros y luego fusionando 3 conjuntos de pares de caras triangulares equiláteras coplanarias en 3 caras rómbicas (60 grados). También puede verse como un tetraedro con 3 de sus 4 vértices rectificados. Las tres caras rómbicas se pliegan para formar la mitad de un hexagrama.
Véase también
Referencias
Enlaces externos
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||