|
Resonancia de LaplaceLa resonancia de Laplace es un caso particular de resonancia orbital en el que tres cuerpos orbitando alrededor de un cuerpo principal, tienen periodos de revolución que guardan entre sí una relación expresada en una fracción de números enteros simples e igual a 1:2:4. Es decir, mientras el cuerpo que tiene una órbita más exterior completa una vuelta, el siguiente en distancia completa dos y el más interior cuatro. En el Sistema Solar solo existe un caso que esté en resonancia de Laplace, el de los satélites galileanos de Júpiter: Ío, Europa y Ganímedes y otro que es muy cercano aunque no llega a serlo, el de los satélites de Urano: Miranda, Ariel y Umbriel. Descripción cinemáticaLa resonancia de Laplace se expresa mediante la siguiente ecuación:[1][2] donde es el movimiento medio de revolución, la inversa del periodo de revolución, y el subíndice indica el orden de los cuerpos de menor a mayor distancia del cuerpo principal. Asimismo, de la anterior deriva otra expresión:[2][3] donde es la longitud media del cuerpo en su órbita. Al ángulo se le denomina ángulo o variable de resonancia y debe tener un valor fijo, lo que indica que dada una posición determinada de los tres cuerpos en un momento dado, dicha posición se debe repetir periódicamente.[4] De la ecuación se deducen las siguientes expresiones:[2] Es decir, el movimiento medio del cuerpo 1 respecto del 2 es dos veces mayor que el movimiento medio del cuerpo 2 respecto del 3 e igualmente el movimiento medio del cuerpo 1 respecto del 3 es tres veces mayor que el movimiento medio del cuerpo 2 respecto del 3. Cada uno de los términos de la ecuación anterior, si fuesen iguales a cero, serían la expresión que deberían cumplir cada una de las parejas de cuerpos 1 - 2 y 2 - 3 si estuvieran en resonancia 2:1, produciéndose de esta manera la conjunción de ambos astros en la misma longitud. Satélites galileanos de Júpiter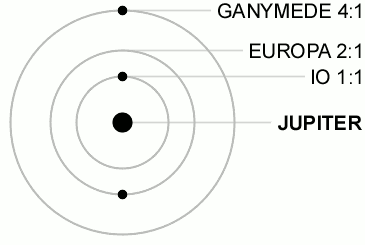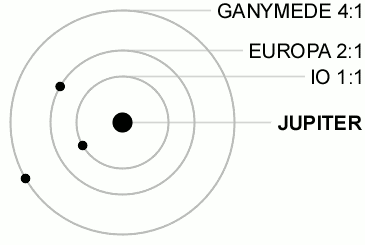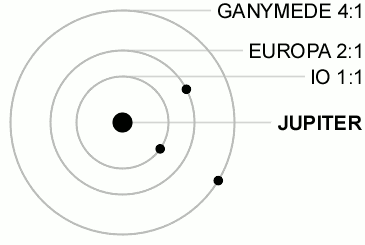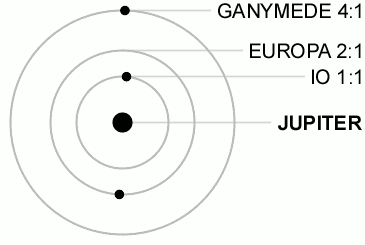 En el caso de los satélites galileanos de Júpiter, Ío, Europa y Ganímedes, se cumple perfectamente la ecuación :[2][4] Asimismo se cumple que la variable de resonancia es 180°:[2] [3] Lo cual quiere decir que si los satélites exteriores Europa y Ganímedes están en conjunción, es decir, y, por conveniencia, iguales a cero, la longitud media del tercer satélite, Ío, será , es decir, estará situado en el lado opuesto de su órbita respecto de los otros dos satélites. Esto quiere decir que nunca se producirá una conjunción triple los satélites galileanos Ío, Europa y Ganímedes. Sin embargo considerando las parejas de satélites Ío - Europa y Europa - Ganímedes, para las que se podría esperar una resonancia exacta 2:1 entre ellos, se comprueba que el resultado de la ecuación no es nulo:[2][4] Es decir, las parejas de satélites Ío - Europa y Europa - Ganímedes no están en una resonancia de movimiento medio de revolución 2:1 exacta. La conjunción de los satélites de cada una de dichas parejas va circulando a lo largo de la órbita del satélite interior completanto una vuelta en un periodo de 1,3 años. Ese valor resulta ser la precesión del periastro, , donde es la longitud del periastro, de las órbitas de Ío en el primer caso y de Europa en el segundo.[1] Es decir, los pares de satélites Ío - Europa y Europa - Ganímedes sí están en resonancia 2:1 siempre que se tenga en cuenta la precesión del periastro de la órbita del cuerpo interior:[1] Conjunciones entre Ío y EuropaDe igual modo se pueden definir las variables de resonancia correspondientes a cada par de resonancias de la forma:[4] Se comprueba que las ecuaciones diferenciales que gobiernan el movimiento de estos satélites tienen una solución particular para los valores:[4] De esta manera, cuando ambos satélites están en conjunción, es decir: , entonces, sustituyendo en las expresiones anteriores se puede comprobar que:[4] Esto quiere decir que las conjunciones entre Ío - Europa tienen lugar cuando Ío está en el periastro de su órbita mientras que Europa está en el apoastro de la suya. De esta manera cuando esto sucede ambos satélites están lo más alejados posible uno de otro. Conjunciones entre Europa y GanímedesIgualmente se definen para el par Europa-Ganímedes las siguientes expresiones de sus variables de resonancia:[4] E igualmente una solución particular para el movimiento de estos satélites implica: Sin embargo en este caso se comprueba que no es una solución estable. De esta manera en las conjunciones entre Europa y Ganímedes, Europa esta en el periastro de su órbita pero Ganímedes puede estar en cualquier punto de la suya. Así, la distancia entre ambos satélites en su conjunto está parcialmente maximizada. Satélites de UranoEn cuanto a los satélites de Urano, Miranda, Ariel y Umbriel, la ecuación no es igual a 0. En concreto se obtiene el valor:[2] Lo que significa que cuando se produce una conjunción entre Ariel y Umbriel, Miranda tiene una posición algo más retrasada respecto a la conjunción anterior, llegando a producirse una conjunción triple cada 12,5 años, un periodo muy largo teniendo en cuenta que los periodos orbitales de estos satélites se miden en unos pocos días. Referencias
|
Portal di Ensiklopedia Dunia





























