Red neuronal residual

Un Bloque Residual en una Red Residual profunda. Aquí la conexión residual se salta dos capas.

Una red neuronal residual (también conocida como red residual, ResNet)[1]​ es un modelo de aprendizaje profundo en el que las capas de pesos aprenden funciones residuales con referencia a las entradas de las capas. Una red residual[1]​ es una red con conexiones de salto que realizan mapeos de identidad, fusionadas con las salidas de las capas por adición. Se comporta como una Highway Network (Autopista de la información)[2]​ cuyas puertas se abren mediante pesos de sesgo fuertemente positivo. Esto permite que los modelos de aprendizaje profundo con decenas o cientos de capas se entrenen fácilmente y se aproximen a una mayor precisión al profundizar. Las conexiones de salto de identidad, a menudo denominadas "conexiones residuales", también se utilizan en las redes LSTM (memoria a corto-largo plazo) de 1997,[3]​ los modelos de transformador (por ejemplo, BERT, modelos GPT como ChatGPT), el sistema AlphaGo Zero, el sistema AlphaStar y el sistema AlphaFold.

Las redes residuales fueron desarrolladas por Kaiming He, Xiangyu Zhang, Shaoqing Ren y Jian Sun, que ganaron el concurso ImageNet 2015.[4]​[5]​

Formulación

Antecedentes

El modelo AlexNet desarrollado en 2012 para ImageNet era una red neuronal convolucional de 8 capas. Las redes neuronales desarrolladas en 2014 por el Visual Geometry Group (VGG) de la Universidad de Oxford se aproximaron a una profundidad de 19 capas apilando capas convolucionales de 3 en 3.[6]​ Pero apilar más capas provocó una rápida reducción de la precisión del entrenamiento,[7]​ lo que se conoce como el problema de la "degradación".[1]​

Una red más profunda no debería producir una mayor pérdida de entrenamiento que su homóloga menos profunda, si esta red más profunda puede construirse mediante su homóloga menos profunda apilada con capas adicionales.[1]​ Si las capas adicionales pueden establecerse como mapeos de identidad, la red más profunda representaría la misma función que la homóloga menos profunda. La hipótesis es que el optimizador no es capaz de aproximarse a los mapeos de identidad para las capas parametrizadas.

Aprendizaje residual

En un modelo de red neuronal multicapa, considere una subred con un número determinado (por ejemplo, 2 o 3) de capas apiladas. Denotemos la función subyacente realizada por esta subred como ${\textstyle H(x)}$, donde ${\textstyle x}$ es la entrada a esta subred. La idea de "aprendizaje residual" re-parametriza esta subred y deja que las capas de parámetros representen una función residual ${\textstyle F(x):=H(x)-x}$. El resultado ${\textstyle y}$ de esta subred se representa como:${\displaystyle {\begin{aligned}y&=F(x)+x\end{aligned}}}$

Este es también el principio de la computación celular[3]​ LSTM de 1997 ${\textstyle y_{t+1}=F(x_{t})+x_{t}}$, que se convierte en ${\textstyle y=F(x)+x}$ durante la retropropagación en el tiempo.

La función ${\textstyle F(x)}$ suele representarse mediante multiplicación de matrices entrelazada con la función de activación y operaciones de normalización (por ejemplo, normalización por lotes o normalización por capas).

Esta subred se denomina "bloque residual".[1]​ Una red residual profunda se construye apilando una serie de bloques residuales.

El funcionamiento de "${\textstyle +\ x}$" en "${\textstyle y=F(x)+x}$" se aborda mediante una conexión de salto que realiza el mapeo de identidad y conecta la entrada de un bloque residual con su salida. Esta conexión suele denominarse "conexión residual" en trabajos posteriores.[8]​

Propagación de la señal

La introducción de mapeos de identidad facilita la propagación de la señal tanto en los trayectos hacia delante como hacia atrás.[9]​

Propagación hacia delante

Si la salida del bloque residual ${\textstyle \ell }$-ésimo es la entrada al bloque residual ${\textstyle (\ell +1)}$-ésimo (es decir, suponiendo que no hay función de activación entre bloques), tenemos:[9]​

${\displaystyle {\begin{aligned}x_{\ell +1}&=F(x_{\ell })+x_{\ell }\end{aligned}}}$

Aplicando esta formulación de forma recursiva, por ejemplo:

${\displaystyle {\begin{aligned}x_{\ell +2}=F(x_{\ell +1})+x_{\ell +1}=F(x_{\ell +1})+F(x_{\ell })+x_{\ell }\end{aligned}}}$, tenemos:

${\displaystyle {\begin{aligned}x_{L}&=x_{\ell }+\sum _{i=l}^{L-1}F(x_{i})\\\end{aligned}}}$

Donde ${\textstyle L}$ es el índice de cualquier bloque residual posterior (por ejemplo, el último bloque) y ${\textstyle \ell }$ es el índice de cualquier bloque anterior. Esta formulación sugiere que siempre hay una señal que se envía directamente desde un bloque menos profundo ${\textstyle \ell }$ a un bloque más profundo ${\textstyle L}$.

Propagación hacia atrás

La formulación del aprendizaje residual ofrece la ventaja añadida de resolver en cierta medida el problema del gradiente de fuga. Sin embargo, es crucial reconocer que el problema del gradiente de fuga no es la causa principal del problema de degradación, puesto que ya se ha abordado mediante el uso de capas de normalización. Tomando la derivada con respecto a ${\textstyle x_{\ell }}$de acuerdo con la propagación hacia adelante anterior, tenemos:[9]​

${\displaystyle {\begin{aligned}{\frac {\partial {\mathcal {E}}}{\partial x_{\ell }}}&={\frac {\partial {\mathcal {E}}}{\partial x_{L}}}{\frac {\partial x_{L}}{\partial x_{\ell }}}\\&={\frac {\partial {\mathcal {E}}}{\partial x_{L}}}\left(1+{\frac {\partial }{\partial x_{\ell }}}\sum _{i=l}^{L-1}F(x_{i})\right)\\&={\frac {\partial {\mathcal {E}}}{\partial x_{L}}}+{\frac {\partial {\mathcal {E}}}{\partial x_{L}}}{\frac {\partial }{\partial x_{\ell }}}\sum _{i=l}^{L-1}F(x_{i})\\\end{aligned}}}$ 

Aquí ${\textstyle {\mathcal {E}}}$ es la función de pérdida que debe minimizarse.

Esta formulación sugiere que el cálculo del gradiente de una capa menos profunda ${\textstyle {\frac {\partial {\mathcal {E}}}{\partial x_{\ell }}}}$ siempre tiene un término ${\textstyle {\frac {\partial {\mathcal {E}}}{\partial x_{L}}}}$ que se añade directamente. Aunque los gradientes del ${\textstyle F(x_{i})}$ son pequeños, el gradiente total ${\textstyle {\frac {\partial {\mathcal {E}}}{\partial x_{\ell }}}}$ no desaparece gracias al término añadido ${\textstyle {\frac {\partial {\mathcal {E}}}{\partial x_{L}}}}$.

Variantes de bloques residuales

Dos variantes de bloques convolucionales residuales[1]​ Izquierda: un bloque básico con dos capas convolucionales de 3x3. Derecha: un bloque de cuello de botella que tiene una capa convolucional 1x1 para reducir la dimensión (por ejemplo, 1/4), una capa convolucional 3x3 y otra capa convolucional 1x1 para restaurar la dimensión.

Bloque básico

Un bloque básico es el bloque de construcción más simple estudiado en la ResNet original.[1]​ Este bloque consta de dos capas convolucionales secuenciales de 3x3 y una conexión residual. Las dimensiones de entrada y salida de ambas capas son iguales.

Bloque cuello de botella

Un bloque cuello de botella[1]​ consta de tres capas convolucionales secuenciales y una conexión residual. La primera capa de este bloque es una convolución 1x1 para reducir la dimensión, por ejemplo, a 1/4 de la dimensión de entrada; la segunda capa realiza una convolución 3x3; la última capa es otra convolución 1x1 para restaurar la dimensión. Los modelos de ResNet-50, ResNet-101 y ResNet-152[1]​ se basan todos en bloques de cuello de botella.

Bloque de preactivación

El bloque residual de preactivación[9]​ aplica las funciones de activación (por ejemplo, no linealidad y normalización) antes de aplicar la función residual ${\textstyle F}$. Formalmente, el cálculo de un bloque residual de preactivación puede escribirse como:

 ${\displaystyle {\begin{aligned}x_{\ell +1}&=F(\phi (x_{\ell }))+x_{\ell }\end{aligned}}}$

Donde ${\textstyle \phi }$ puede ser cualquier operación de activación no lineal (por ejemplo, ReLU) o de normalización (por ejemplo, LayerNorm). Este diseño reduce el número de mapeos no identitarios entre bloques residuales. Este diseño se utilizó para entrenar modelos con 200 a más de 1000 capas.[9]​

Desde GPT-2, los bloques transformadores se han implementado dominantemente como bloques de pre-activación. Esto se denomina a menudo "prenormalización" en la literatura de los modelos transformador.[10]​

Bloque transformador

La arquitectura de Transformador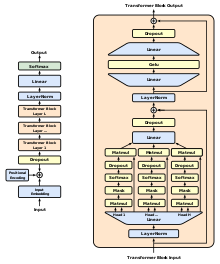 utilizada en el modelo GPT original. Un Bloque Transformador consta de dos Bloques Residuales: un Bloque de Atención Multicabezal y un Bloque Perceptrón Multicapa (MLP) feed-forward.

Un bloque transformador es una pila de dos bloques residuales. Cada bloque residual tiene una conexión residual.

El primer bloque residual es un bloque de atención multicabeza, que realiza un cálculo de (auto)atención seguido de una proyección lineal.

El segundo bloque residual es un bloque de perceptrón multicapa (MLP) feed-forward (alimentación anticipada). Este bloque es análogo a un bloque de cuello de botella "inverso": tiene una capa de proyección lineal (que equivale a una convolución 1x1 en el contexto de las redes neuronales convolucionales) que aumenta la dimensión, y otra proyección lineal que reduce la dimensión.

Un bloque transformador tiene una profundidad de 4 capas (proyecciones lineales). El modelo GPT-3 tiene 96 Bloques transformadores (en la literatura sobre transformadores, un bloque de transformador se denomina a menudo "Transformer Layer" (capa de transformador)). Este modelo tiene una profundidad de unas 400 capas de proyección, incluidas 96x4 capas en bloques transformadores y algunas capas adicionales para la incrustación de entrada y la predicción de salida.

Los modelos transformador muy profundos no pueden entrenarse con éxito sin conexiones residuales.[11]​

Trabajos relacionados

En el libro[12]​ escrito por Frank Rosenblatt, publicado en 1961, se presentaba un modelo de perceptrón multicapa (MLP) de tres capas con conexiones de salto (Capítulo 15, p313 en[12]​). El modelo se denominaba "sistema de acoplamiento cruzado", y las conexiones de salto eran formas de conexiones de acoplamiento cruzado.

En dos libros publicados en 1994[13]​ y 1996,[14]​ se presentaron las conexiones "skip-layer" (salto de capa) en los modelos MLP feed-forward: "La definición general [de MLP] permite más de una capa oculta, y también permite conexiones skip-layer desde la entrada a la salida" (p261 en,[13]​ p144 en[14]​), "... lo que permite a las unidades no lineales perturbar una forma funcional lineal" (p262 en[13]​). Esta descripción sugiere que el MLP no lineal funciona como una función residual (perturbación) añadida a una función lineal.

Sepp Hochreiter analizó el problema del gradiente evanescente en 1991 y le atribuyó la razón por la que el aprendizaje profundo no funcionaba bien.[15]​ Para superar este problema, las redes neuronales recurrentes de memoria a largo plazo (LSTM)[3]​ tenían conexiones de salto o conexiones residuales con un peso de 1,0 en cada celda LSTM (llamado carrusel de error constante) para calcular ${\textstyle y_{t+1}=F(x_{t})+x_{t}}$.Durante la retropropagación a través del tiempo, esto se convierte en la fórmula residual antes mencionada ${\textstyle y=F(x)+x}$ para redes neuronales feedforward. Esto permite entrenar redes neuronales recurrentes muy profundas con un intervalo de tiempo t muy largo. Una versión posterior de LSTM publicada en 2000[16]​ modula las conexiones LSTM de identidad mediante las llamadas puertas de olvido, de forma que sus pesos no están fijados a 1,0, sino que pueden aprenderse. En los experimentos, las puertas de olvido se inicializaron con pesos de sesgo positivo,[16]​ por lo que se abrieron, abordando el problema del gradiente de fuga.

La red Highway Network de mayo de 2015[2]​[17]​ aplica estos principios a las redes neuronales feedforward. Se dice que es "la primera red feedforward muy profunda con cientos de capas".[18]​ Es como una LSTM con puertas de olvido desplegadas en el tiempo,[16]​ mientras que las redes residuales posteriores no tienen puertas de olvido equivalentes y son como la LSTM original desplegada.[3]​ Si las conexiones de salto en las ighway network son "sin puertas", o si sus puertas se mantienen abiertas (activación 1,0) a través de fuertes pesos de sesgo positivo, se convierten en las conexiones de salto de identidad en las redes residuales.

El artículo original Highway Network[2]​ no sólo introdujo el principio básico de las redes feedforward muy profundas, sino que también incluyó resultados experimentales con redes de 20, 50 y 100 capas, y mencionó experimentos en curso con hasta 900 capas. Las redes con 50 o 100 capas presentaron un error de entrenamiento menor que sus homólogas de red simple, pero no menor que su homóloga de 20 capas (en el conjunto de datos MNIST, Figura 1 en[2]​). No se observó ninguna mejora en la precisión de las pruebas con redes de más de 19 capas (en el conjunto de datos CIFAR-10; Tabla 1 en[2]​). Sin embargo, el artículo de ResNet[9]​ aportó pruebas experimentales sólidas de las ventajas de profundizar más de 20 capas. Argumentaba que el mapeo de identidad sin modulación es crucial y mencionaba que la modulación en la conexión de salto puede llevar a señales de fuga en la propagación hacia delante y hacia atrás (Sección 3 en[9]​). Esta es también la razón por la que las puertas de olvido de la LSTM de 2000[16]​ se abrieron inicialmente mediante pesos de sesgo positivo: mientras las puertas estén abiertas, se comporta como la LSTM de 1997. Del mismo modo, una Highway Net cuyas puertas se abren mediante pesos de sesgo fuertemente positivos se comporta como una ResNet. Las conexiones de salto utilizadas en las redes neuronales modernas (por ejemplo, Transformadores) son dominantemente mapeos de identidad.

Las DenseNets de 2016[19]​ se diseñaron como redes neuronales profundas que intentan conectar cada capa con todas las demás. DenseNets abordó este objetivo mediante el uso de mapeos de identidad como conexiones de salto. A diferencia de las ResNets, las DenseNets fusionan la salida de la capa con conexiones de salto por concatenación, no por adición.

Las redes neuronales con Profundidad Estocástica[20]​ fueron posibles gracias a las arquitecturas de red residual. Este procedimiento de entrenamiento deja caer aleatoriamente un subconjunto de capas y permite que la señal se propague a través de la conexión de salto de identidad. También conocido como "DropPath", se trata de un método de regularización eficaz para entrenar modelos grandes y profundos, como el Vision Transformer (ViT).

Relación biológica

En el artículo original sobre las redes residuales no se afirmaba que estuvieran inspiradas en sistemas biológicos. Pero investigaciones posteriores han relacionado las redes residuales con algoritmos biológicamente plausibles.[21]​[22]​

Un estudio publicado en Science en 2023[23]​ reveló el conectoma completo del cerebro de un insecto (de una larva de mosca de la fruta). Este estudio descubrió "atajos multicapa" a los que se asemejan las conexiones de salto de las redes neuronales artificiales, incluidas las ResNets.

Véase también

• Circuito neuronal
• Red neuronal artificial
• Isolation forest

Referencias

1. He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015). Deep Residual Learning for Image Recognition. 
2. Srivastava, Rupesh Kumar; Greff, Klaus; Schmidhuber, Jürgen (2015). Highway Networks. 
3. Sepp Hochreiter; Jürgen Schmidhuber (1997). «Long short-term memory». Neural Computation: 1735-1780. PMID 9377276. doi:10.1162/neco.1997.9.8.1735. 
4. «Imagenet: A large-scale hierarchical image database». scholar.google.com. Consultado el 21 de agosto de 2023. 
5. «ILSVRC2015 Results». image-net.org. Consultado el 21 de agosto de 2023. 
6. Simonyan, Karen; Zisserman, Andrew (2014). Very Deep Convolutional Networks for Large-Scale Image Recognition. 
7. He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2016). Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. 
8. Szegedy, Christian; Ioffe, Sergey; Vanhoucke, Vincent; Alemi, Alex (2016). Inception-v4, Inception-ResNet and the impact of residual connections on learning. 
9. He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2015). Identity Mappings in Deep Residual Networks. 
10. Radford, Alec; Wu, Jeffrey; Child, Rewon; Luan, David; Amodei, Dario; Sutskever, Ilya (2019). Language models are unsupervised multitask learners. 
11. Dong, Yihe; Cordonnier, Jean-Baptiste; Loukas, Andreas (2021). Attention is not all you need: pure attention loses rank doubly exponentially with depth. 
12. Rosenblatt, Frank (1961). Principles of neurodynamics. perceptrons and the theory of brain mechanisms. 
13. Venables, William N.; Ripley, Brian D. (1994). Modern Applied Statistics with S-Plus (en inglés). Springer-Verlag. ISBN 978-3-540-94350-1. Consultado el 22 de agosto de 2023. 
14. Ripley, Brian D. (1996). Pattern Recognition and Neural Networks. Cambridge University Press. ISBN 978-0-521-71770-0. Consultado el 22 de agosto de 2023. 
15. Hochreiter, Sepp (1991). «Untersuchungen zu dynamischen neuronalen Netzen». Technical University Munich, Institute of Computer Science. 
16. Felix A. Gers; Jürgen Schmidhuber; Fred Cummins (2000). «Learning to Forget: Continual Prediction with LSTM». Neural Computation: 2451-2471. PMID 11032042. doi:10.1162/089976600300015015. 
17. Srivastava, Rupesh Kumar; Greff, Klaus; Schmidhuber, Jürgen (2015). Training Very Deep Networks. 
18. «Microsoft Wins ImageNet 2015 through Feedforward LSTM without Gates». people.idsia.ch. Consultado el 22 de agosto de 2023. 
19. Huang, Gao; Liu, Zhuang; van der Maaten, Laurens; Weinberger, Kilian (2016). Densely Connected Convolutional Networks. 
20. Huang, Gao; Sun, Yu; Liu, Zhuang; Weinberger, Kilian (2016). Deep Networks with Stochastic Depth. 
21. Liao, Qianli; Poggio, Tomaso (2016). Bridging the Gaps Between Residual Learning, Recurrent Neural Networks and Visual Cortex. 
22. Xiao, Will; Chen, Honglin; Liao, Qianli; Poggio, Tomaso (2018). Biologically-Plausible Learning Algorithms Can Scale to Large Datasets. 
23. Winding, Michael; Pedigo, Benjamin; Barnes, Christopher; Patsolic, Heather; Park, Youngser; Kazimiers, Tom; Fushiki, Akira; Andrade, Ingrid; Khandelwal, Avinash; Valdes-Aleman, Javier; Li, Feng; Randel, Nadine; Barsotti, Elizabeth; Correia, Ana; Fetter, Fetter; Hartenstein, Volker; Priebe, Carey; Vogelstein, Joshua; Cardona, Albert; Zlatic, Marta (2023). «The connectome of an insect brain». Science. PMC 7614541. PMID 36893230. doi:10.1126/science.add9330. 

• Datos: Q43744058