Red Zobel

Las redes Zobel son un tipo de sección de filtrado basadas en el principio de diseño de la impedancia de imagen. Son llamadas así en honor a Otto Julius Zobel de Bell Labs, quien en 1923 publicó un artículo sobre filtros de imagen que gozaría de una gran difusión.[1]​ La característica principal de las redes Zobel es que la impedancia de entrada es fija en el diseño, independientemente de la función de transferencia. Esta característica se logra a expensas de un mayor número de componentes a usar en comparación de otros tipos de secciones de filtrado. La impedancia normalmente sería especificada siendo constante y puramente resistiva. Por tal razón, también son conocidas como redes de resistencias. Sin embargo, cualquier impedancia obtenible con componentes discretos es también posible de implementar.

Las redes Zobel fueron formalmente usadas en las telecomunicaciones para aplanar y hacer más ancha la respuesta en frecuencia de las líneas de cobre, produciendo así una línea de alta calidad de una originalmente diseñada para uso telefónico. Sin embargo, con los avances de la tecnología digital, son ahora poco usadas.

Cuando se usa una red Zobel para cancelar la porción reactiva de la impedancia de un altavoz, el diseño a veces es conocido como una celda de Boucherot. En este caso, solo se implementa la mitad de la red con componentes fijos, la otra mitad siendo la impedancia real e imaginaria de los componentes del altavoz. Esta red es similar a los circuitos de corrección del factor de potencia usados en la distribución de energía eléctrica, por lo tanto su asociación con el nombre de Boucherot.

Una forma común de las redes Zobel, es el puente T. Este término es usualmente tomado para implicar el uso de una red Zobel, a veces incorrectamente usado cuando el circuito implementado es en realidad algo diferente un puente T.

Derivación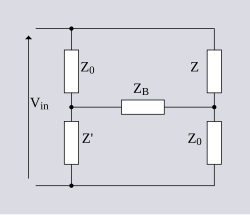

Red Zobel como un puente balanceado

La base de una red Zobel es un circuito de puente balanceado como es mostrado en la derecha. La condición para el balance es la siguiente;

${\displaystyle {\frac {Z}{Z_{0}}}={\frac {Z_{0}}{Z'}}}$

Si esto es expresado en términos de una Z₀ = 1 normalizada como es convencionalmente hecho en tablas de filtros, entonces el balance es simplemente;

${\displaystyle Z={\frac {1}{Z'}}}$

En otras palabras, ${\displaystyle \scriptstyle Z'}$ es simplemente el inverso, o impedancia dual de ${\displaystyle \scriptstyle Z}$.

La impedancia de puenteo Z_B está situada a través de los puntos de balance y por lo tanto no tiene potencial. Consecuentemente, no pedirá corriente y su valor no hará diferencia a la función del circuito. Sin embargo, su valor es casi siempre escogido a ser Z₀ por razones que se clarificarán en la discusión de los circuitos puente T.

Impedancia de entrada

La impedancia de entrada está dada por

${\displaystyle {\frac {1}{Z_{\text{in}}}}={\frac {1}{Z_{0}+Z'}}+{\frac {1}{Z+Z_{0}}}}$

Sustituyendo la condición de balance,

${\displaystyle Z'={\frac {Z_{0}^{2}}{Z}}}$

da

${\displaystyle Z_{\text{in}}=Z_{0}}$

La impedancia de entrada puede ser arreglada para ser puramente resistiva acomodando a

${\displaystyle Z_{0}=R_{0}\!\,}$

La impedancia de entrada será entonces real e independiente de la frecuencia angular dentro y fuera de la banda, sin importar la complejidad de la sección de filtrado.

Función de transferencia

Circuito equivalente de la red Zobel para calcular la ganancia

Si la Z₀ en la parte inferior derecha del puente es tomada para ser la carga de salida, entonces la función de transferencia V_in/V_o puede ser calculada para la sección. Solo la rama rhs necesita ser considerada en este cálculo. La razón de esto puede ser visto al considerar que no hay corriente a través de R_B. Nada de la corriente que fluye a través de la rama lhs va a ir hacia la carga. Es decir, se afecta la impedancia de entrada (y por lo tanto el voltaje de la terminal de entrada) pero no a la función de transferencia. La anterior ahora puede ser fácilmente encontrada como;

${\displaystyle A(\omega )={\frac {Z_{0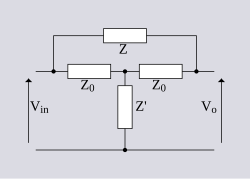}}{Z+Z_{0}}}}$

Implementación del puente T

Implementación del puente Zobel T

La impedancia de carga, es de hecho la impedancia de la siguiente etapa o la de la línea de transmisión y puede ser sensiblemente omitida del diagrama del circuito. Así mismo, si ponemos;

${\displaystyle Z_{B}=Z_{0}\,\!}$

Entonces resulta el circuito de la derecha. Esto es referido como el circuito puenteado T o puente T, dado que la impedancia Z es vista como puente a través de la sección T. El propósito de poner Z_B = Z₀ es el de hacer la sección del filtro simétrica. Esto tiene la ventaja de que entonces presentará la misma impedancia Z₀, en los puertos de entrada y de salida.

Tipos de sección

Una sección de filtro Zobel puede ser implementada para ser pasa-bajas, pasa-altas, pasa-bandas o rechaza-bandas. También es posible implementar un atenuador de respuesta en frecuencia plana. Esto último es de importancia para las secciones de filtros prácticos descritos después.

Atenuador

Z y Z'  para un atenuador Zobel

Para una sección de atenuador, Z es simplemente

${\displaystyle Z=R\,\!}$

y,

${\displaystyle Z'=R'={\frac {R_{0}^{2}}{R}}}$

La atenuación de la sección está dada por;

${\displaystyle L=20\log \left({\frac {R}{R_{0}}}+1\right)\,{\text{dB}}}$

Pasa-Bajas

Z y Z ' para una sección de filtro pasa-bajas Zobel

Para una sección de filtro pasa-bajas, Z es un inductor y Z&rnbsp;' es un capacitor;

${\displaystyle Z=i\omega L\!\,}$

y

${\displaystyle Z'={\frac {1}{i\omega C'}}}$

donde

${\displaystyle C'={\frac {L}{R_{0}^{2}}}}$

La función de transferencia de la sección está dada por

${\displaystyle A(\omega )={\frac {R_{0}}{i\omega L+R_{0}}}}$

El punto de los 3dB ocurre cuando ωL = R₀, por lo que la frecuencia de corte de los 3dB está dada por

${\displaystyle \omega _{c}={\frac {R_{0}}{L}}}$

donde ω está en la banda de rechazo sobre ω_c,

${\displaystyle A(\omega )\approx {\frac {R_{0}}{i\omega L}}}$

Puede ser visto de esto que A(ω) cae en la banda de rechazo clásica 6dB/8.ª (o 20dB/década).

Pasa Altas

Z y Z' para una sección de filtro pasa altas Zobel

Para una sección de filtro pasa altas, Z es un capacitor y Z' un inductor:

${\displaystyle Z={\frac {1}{i\omega C}}}$

y

${\displaystyle Z'=i\omega L'\!\,}$

donde

${\displaystyle L'=CR_{0}^{2}\!\,}$

La función de transferencia de la sección está dada por

${\displaystyle A(\omega )={\frac {i\omega CR_{0}}{1+i\omega CR_{0}}}}$

El punto de los 3dB ocurre cuando ωC = ^1⁄_R0 por lo que la frecuencia de corte de los 3dB está dada por

${\displaystyle \omega _{c}={\frac {1}{CR_{0}}}}$

En la banda de tope

${\displaystyle A(\omega )\approx i\omega CR_{0}}$

cayendo a 6dB/8.ª.

Pasa Bandas

Z y Z'  para una sección filtro pasa banda de Zobel

Para una sección de filtro pasa bandas, Z es un circuito en serie resonante y Z ' es un circuito resonante desviado;

${\displaystyle Z=i\omega L+{\frac {1}{i\omega C}}}$

y

${\displaystyle Y'={\frac {1}{Z'}}=i\omega C'+{\frac {1}{i\omega L'}}}$

La función de transferencia está dada por

${\displaystyle A(\omega )={\frac {i\omega CR_{0}}{1+i\omega CR_{0}-\omega ^{2}LC}}}$

El punto de los 3dB ocurre cuando |1 − ω^2LC| = ωCR₀ por lo que la frecuencia de corte de los 3dB está dada por

${\displaystyle \omega _{c}={\frac {1}{2LC}}\left(\pm R_{0}C+{\sqrt {R_{0}^{2}C^{2}+4LC}}\right)}$

de la cual la frecuencia central, ω_m, y el ancho de banda, Δω, pueden ser determinados como:

${\displaystyle {\begin{aligned}\Delta \omega &={\frac {R_{0}}{L}}\\\omega _{m}&={\sqrt {{\frac {R_{0}^{2}}{4L^{2}}}+{\frac {1}{LC}}}}\end{aligned}}}$

Nótese que esto es diferente de la frecuencia resonante

${\displaystyle \omega _{0}={\sqrt {\frac {1}{LC}}}}$

la relación entre ellas dada por

${\displaystyle \omega _{m}^{2}=\left({\frac {\Delta \omega }{2}}\right)^{2}+\omega _{0}^{2}}$

Rechaza Banda

Z y Z'  para una sección de filtro rechaza bandas Zobel

Para una sección de filtro rechaza bandas, Z es un circuito de resonancia desviada y Z' es un circuito resonante en serie:

${\displaystyle Y={\frac {1}{Z}}=i\omega C+{\frac {1}{i\omega L}}}$

y

${\displaystyle Z'=i\omega L'+{\frac {1}{i\omega C'}}}$

La función de transferencia y el ancho de banda puede ser encontrado por analogía con la sección pasa bandas.

${\displaystyle \Delta \omega ={\frac {1}{CR_{0}}}}$

Y,

${\displaystyle \omega _{m}={\sqrt {\left({\frac {1}{2R_{0}C}}\right)^{2}+{\frac {1}{LC}}}}}$

Secciones prácticas

Las redes Zobel rara vez son utilizadas para el filtrado de frecuencias tradicional, ya que otros tipos de filtro resultan significativamente más eficientes para este propósito. Donde las redes Zobel sobresalen es en las aplicaciones de ecualización de frecuencia, particularmente en las líneas de transmisión. La dificultad con las líneas de transmisión es que la impedancia de la línea varía de una manera compleja a través de la banda y es tediosa de medir. Para la mayoría de tipos de filtro, esta variación en la impedancia causa una diferencia significativa en comparación a los valores teóricos, y es matemáticamente tedioso de compensar, incluso asumiendo que la impedancia es conocida precisamente. Pero si se utilizan las redes Zobel, basta con medir la respuesta de la línea en una carga resistiva y después diseñar un ecualizador que la compense. No existe ninguna necesidad de saber algo sobre la impedancia de la línea, ya que la red Zobel presentará exactamente la misma impedancia de la línea que será medida por los instrumentos. Su respuesta será, por lo tanto, precisamente como se prediga teóricamente. Esto es una gran ventaja cuando las líneas de alta calidad con respuestas en frecuencia planas son deseadas.

Pérdida básica

Una sección práctica pasa altas, incorporando pérdida básica usada para corregir el debilitamiento de alto nivel.

Para las líneas de audio, es invariablemente necesario el combinar componentes L/C con atenuadores resistivos en la misma sección. La razón de esto es que la estrategia de diseño usual es requerir que la sección atenúe todas las frecuencias al nivel de la frecuencia más baja en el pasa bandas. Sin los componentes resistivos, el filtro, al menos en teoría, incrementaría su atenuación sin límite. La atenuación en la banda de rechazo del filtro (es decir, el límite de la atenuación máxima) es referida como la “pérdida básica” (roll-off) de la sección. En otras palabras, la parte plana de la banda es atenuada por la pérdida básica hasta el nivel de la parte en caída de la banda que se requiere ecualizar. La siguiente discusión de las secciones prácticas, se relaciona en particular a las líneas de transmisión de audio.

Roll-off de 6dB/octava

respuesta de Red Zobel pasa altas para varias pérdidas básicas.Normalizado a ${\displaystyle \scriptstyle R_{0}\;=\;1}$ y ${\displaystyle \scriptstyle \omega _{c}\;=\;1}$

El efecto más significativo que debe ser compensado es que en cierta frecuencia de corte la respuesta de la línea empieza a disminuir como un simple filtro pasa-bajas. El ancho de banda efectivo de la línea puede ser incrementado con una sección que sea un filtro pasa altas (y que iguale a tal sección de disminución), en combinación con un atenuador. En la parte plana del pasa bandas solo la parte de atenuación de la sección del filtro es significativa. Esto es puesto tal que se tenga una atenuación igual al nivel de la frecuencia más alta de interés. Todas las frecuencias hasta este punto serán ecualizadas de forma plana a un nivel atenuado. Sobre este punto, la salida del filtro volverá a disminuir.

Líneas con error de posición

Muy comúnmente en las redes de telecomunicaciones, un circuito está hecho de dos secciones de línea que no tienen la misma impedancia característica. Por ejemplo 150 Ω y 300 Ω. Un efecto de esto es que la disminución puede empezar en 6db/octava en la frecuencia de corte inicial ${\displaystyle \scriptstyle f_{c1}}$, pero después en ${\displaystyle \scriptstyle f_{c2}}$ se puede volver mucho más inclinada. Esta situación requiere entonces de al menos dos secciones pasa altas para compensar que cada una opera en diferentes ${\displaystyle \scriptstyle f_{c}}$.

Topes y caídas

Los topes y caídas en un pasa bandas pueden ser compensadas con secciones rechaza bandas y pasa bandas respectivamente. Un elemento atenuador es también requerido, pero usualmente más pequeño que el necesario para la disminución de roll-off. Tales anomalías en el pasa bandas pueden ser causadas por segmentos de línea mal posicionados como se describe arriba. Las caídas también pueden ser causadas por variaciones de la temperatura de tierra.

Disminución (roll-off) del transformador

Ocasionalmente, una sección pasa bajas es incluida para compensar por la disminución excesiva de línea de transformador en el final de la frecuencia baja. Sin embargo, este efecto es usualmente muy pequeño en comparación de los efectos mencionados arriba.

Las secciones de frecuencias bajas usualmente tienen inductores de valores altos. Tales inductores tienen muchas vueltas y consecuentemente tienden a tener una resistencia significativa. Para mantener la sección de resistencia constante en la entrada, la rama dual del puente T debe contener una resistencia dual a la desviada, es decir, una resistencia en paralelo al capacitor. Aún con la compensación, la resistencia desviada tiene el efecto de insertar atenuación en frecuencias bajas. Esto a su vez tiene el efecto de levemente reducir la cantidad de carga LF que la sección de otra manera habría producido.

La compensación de la resistencia del inductor no es un problema tan grande a frecuencias altas, donde los inductores tienden a ser más pequeños. De cualquier modo, para una sección pasa altas el inductor está en serie con la resistencia de pérdida básica y la resistencia desviada puede ser restada de tal resistencia. Por otra parte, la técnica de compensación puede ser requerida por secciones resonantes, especialmente un resonador de alta Q siendo usado para levantar una muy estrecha banda. Para tales secciones el valor de los inductores también puede ser alto.

Compensación de temperatura

Una atenuación ajustable de filtro pasa altas puede ser usada para compensar cambios en la temperatura de la tierra. La temperatura de la tierra cambia muy lentamente en comparación con la temperatura de la superficie. Los ajustes son usualmente solo requeridos de 2 a 4 veces por año para aplicaciones de audio.

Una colección de varios diseños de compensación de temperatura. Algunos pueden ser ajustados con links conectables, otros requieren soldarse. El ajuste no es muy frecuente.

Los componentes internos de un ecualizador de temperatura: El inductor y capacitor en la derecha ajustan la frecuencia a la que el ecualizador empieza a operar, los bancos de resistencia seleccionable en la izquierda ponen la pérdida básica y por lo tanto la cantidad de ecualización

Cadena de filtrado típica

Un filtro completo típico consistirá de un número de secciones Zobel para la disminución (roll off), las caídas de frecuencia y temperatura seguidas por una sección de atenuador plano para bajar el nivel a la atenuación estándar. Esto es seguido por una amplificador de ganancia fija para traer de vuelta la señal a un nivel utilizable. Típicamente 0dBu. La ganancia del amplificador es usualmente no mayor a 45dB máximo. Si se usa más que la anterior, la amplificación del ruido tenderá a cancelar los beneficios de calidad de un ancho de banda mejorado. Este límite en la amplificación esencialmente disminuye cuanto del ancho de banda será incrementado por tales técnicas. También debería ser notado que ninguna parte de la banda de la señal de entrada será amplificada por completo a 45dB. Los 45dB están formados por la pérdida de línea en la parte plana de su espectro más la pérdida básica de cada sección. En general, cada sección tendrá una pérdida mínima en una banda de frecuencia diferente, por lo tanto la amplificación en tal banda será limitada a la pérdida básica de solo esa sección del filtro, asumiendo en los anteriores sobre cruce insignificante. Una elección típica para R₀ es 600 Ω. Un transformador de buena calidad (usualmente esencial, pero no mostrado en el diagrama), conocido como bobina de repetición, se encuentra en el inicio de la cadena donde la línea termina.

Un ejemplo de una cadena de redes Zobel típicas siendo usadas para ecualización de línea

Implementaciones de otras secciones

Además del puente T, hay otras formas de secciones posibles que pueden ser usadas.

Secciones L

Circuito abierto derivado de la sección L para una sección pasa altas con pérdida básica

Corto circuito derivado de la sección L para una sección pasa altas con pérdida básica

Como se mencionó arriba, ${\displaystyle \scriptstyle Z_{B}}$ puede ser puesta a cualquier impedancia deseada sin afectar la impedancia de entrada. En particular, poniéndola como un circuito abierto o un corto circuito resulta en una sección simplificada del circuito llamada L. Estas son mostradas arriba para el caso de una sección pasa altas con pérdida básica.

El puerto de entrada aún presenta una impedancia de ${\displaystyle \scriptstyle R_{0}}$ (proveyendo que la salida es terminada en ${\displaystyle \scriptstyle R_{0}}$) pero el puerto de salida no presenta una impedancia constante. Los circuitos abiertos y corto circuitos son capaces de ser revertidos para que ${\displaystyle \scriptstyle R_{0}}$ sea representada en la salida y la impedancia vairable sea presentada en la entrada.

Para mantener el beneficio de las redes Zobel (impedancia constante), el puerto de impedancia variable no debe estar cerca de la impedancia de línea, ni debe estar cerca del puerto de impedancia variable de otra sección. Estar cerca del amplificador es aceptable, dado que la impedancia de entrada para el amplificador normalmente se pone en ${\displaystyle \scriptstyle R_{0}}$ dentro del rango de tolerancias aceptables. En otras palabras, la impedancia variable no debe estar cerca de otras impedancias variables.

Un puente T balanceado pasa altas con pérdida básica

Puente T balanceado

Las redes Zobel aquí descritas pueden ser usadas para ecualizar líneas de piso compuestas de par trenzado o cables star quad. La naturaleza del circuito balanceado de tales líneas ofrece un buen CMRR. Para mantener el CMRR, los circuitos conectados a la línea deben mantener el balance. Por tal razón, versiones balanceadas de las redes Zobel son a veces requeridas. Esto es logrado al obtener la impedancia de los componentes en serie y después poner componentes idénticos en la rama de retroalimentación del circuito.

Un pasa altas Zobel de corto circuito en la sección C y con pérdida básica.

Secciones C balanceadas

Una sección C es una versión balanceada de una sección L. El balance es logrado en la misma manera que una sección de puente T balanceado, es decir, se pone la mitad de la impedancia en serie en el conductor común. Las secciones C y L pueden venir en variaciones de circuito abierto o corto circuito. Las mismas restricciones aplican para secciones C en cuestión de la impedancia de las terminaciones en las secciones L.

Sección X

Es posible transformar una sección de puente T en una Lattice o sección X.[2]​ La sección X es un tipo de circuito puente, pero es usualmente representado como un lattice y por lo tanto su nombre. Su topología lo hace intrínsecamente balanceado pero nunca es usado para implementar los filtros de resistencia constante descritos aquí debido al incrementado número de componentes. Lo anterior surge debido al proceso de transformación y no el de balance. Sin embargo, hay una aplicación en común para esta topología, el ecualizador de fase lattice, que también es de resistencia constante e inventado por Zobel. El circuito difiere de los descritos aquí en que el circuito puenteado, en que generalmente no se encuentra balanceado.

Secciones a la mitad

Con respecto a a los filtros de resistencia constante, el término de sección a la mitad tiene un significado un tanto distinto en otros tipos de filtros de imágenes. Generalmente, una sección a la mitad es formada al cortar por el punto medio de la impedancia en serie y de la admitancia desviada de una sección completa de una red escalonada. Es por lo tanto es literalmente una sección a la mitad. Sin embargo, aquí hay una definición un tanto distinta. Una sección a la mitad es la impedancia en serie o admitancia desviada tal que cuando se conecta entre las impedancias de carga o de fuente de R₀, resultará en la misma función de transferencia que la de un circuito de resistencia constante arbitraria. El propósito de usar secciones a la mitad es que la misma funcionalidad es lograda con un conteo drásticamente reducido de componentes.

Si un circuito de resistencia constante tiene una entrada V_in, entonces un generador con impedancia R₀ debe tener un voltaje de circuito abierto de E=2V_in para que pueda producir V_in en la entrada del circuito de resistencia constante. Si el circuito de resistencia constante se reemplaza por una impedancia de 2Z, como en el diagrama de arriba, se puede ver por simple simetría que el voltaje V_in aparecerá a la mitad de la impedancia 2Z. La salida de tal circuito puede ahora ser calculada como,

${\displaystyle {\frac {V_{O}}{V_{in}}}={\frac {R_{0}}{Z+R_{0}}}}$

que es precisamente lo mismo que la sección de puente T con el elemento en serie Z. La sección a a la mitad en serie es por lo tanto una impedancia en serie de 2Z. Por tal razonamiento, la sección a la mitad desviada es de impedancia desviada ^1⁄₂Z' (o el doble de la admitancia). Debe ser enfatizado que tales secciones a la mitad distan de ser de. tipo resistencia constante. Tienen la misma función de transferencia que una red de resistencia constante, pero solo cuando están correctamente terminadas. Un ecualizador no dará buenos resultados si una sección a la mitad está posicionada viendo hacía la línea, debido a que la línea tendrá una impedancia variable y posiblemente desconocida. Del mismo modo, dos secciones a la mitad no pueden ser conectadas directamente una de la otra, ya que ambas tendrán impedancias variables. Sin embargo, si un atenuador suficientemente grande se pone entre dos impedancias variables, esto tendrá el efecto de enmascaramiento. Un atenuador de alto valor tendrá una impedancia de entrada ${\displaystyle \scriptstyle \approx R_{0}}$ sin importar la impedancia terminante en el otro lado. En el ejemplo de la cadena práctica mostrado arriba, se requiere un atenuador de 22dB. No es necesario ponerlo al final de la cadena, puede ser puesto donde sea y usado para enmascarar 2 impedancias mal colocadas, así mismo, puede ser dividida en una o más partes para enmascarar más de una mala colocación.

Redes Zobel y controladores de altavoces

Red Zobel corrigiendo la impedancia del altavoz

Las redes Zobel pueden ser usadas para hacer que la impedancia que presentan los altavoces aparezca como una resistencia constante. Esto es benéfico para el desempeño del amplificador. La impedancia de un altavoz es en parte resistiva. La resistencia siendo representada como la energía transferida de un amplificador al sonido de salida. Sin embargo, el altavoz también presenta inductancia debido a las vueltas de la bobina. La impedancia de un altavoz es por lo tanto representada y modelada como un inductor y resistencia en serie. Un circuito en paralelo de una resistencia en serie con un capacitor de los valores correctos, formará un puente Zobel. Es obligatorio el usar ${\displaystyle \scriptstyle R_{B}\;=\;\infty }$ dado que el punto central entre el inductor y la resistencia es inaccesible ( y de hecho ficticio, la resistencia y el inductor son cantidades distribuidas como una línea de transmisión). El altavoz puede ser modelado más precisamente por un circuito equivalente complejo. Por consiguiente, la red Zobel compensante también se volvería más compleja en cierto grado.[3]​

Notar que el circuito trabajará de igual manera si el capacitor y la resistencia son intercambiadas. En este caso, el circuito ya no es un puente Zobel balanceado, pero claramente la impedancia no ha cambiado. El mismo circuito pudo ser encontrado diseñándolo desde el punto de vista de minimización del poder reactivo de Paul Boucherot. Desde este abordaje en el diseño no hay diferencia en el orden del capacitor y la resistencia y la celda de Boucherot puede ser considerada como una mejor descripción.

Ecualizadores de video

Las redes Zobel pueden ser usadas para la ecualización tanto de líneas de audio como de video. Hay sin embargo, una técnica diferente para los dos tipos de señal. La diferencia radica en que las características del cable pueden ser resumidas de la siguiente manera;

• El video comúnmente usa cable co-axial el cual requiere de una topología desbalanceada para los filtros, mientras que el audio comúnmente usa un par trenzado, el cual requiere de una topología balanceada.
• El video requiere de un ancho de banda más grande y una fase diferencial de más estrechas especificaciones, lo cual a su vez resulta en una especificación dimensional nueva con requerimientos de mayor precisión para el cable.
• La especificación más estrecha para los cables de video tiende a producir una substancialmente constante impedancia característica sobre una banda ancha (usualmente nominalmente 75 Ω). Por otra parte, el cable de audio puede nominalmente ser 600 Ω (300 Ω y 150 Ω también son valores estándares), pero solo se medirá prácticamente tal valor en 800 Hz. A frecuencias más bajas será mucho más alto y a frecuencias altas será más pequeño y más reactivo.

Gráfica de la respuesta de una línea de video mostrando la típica ${\displaystyle \scriptstyle {\sqrt {f}}}$ response

• Tales características resultarán en una respuesta de mayor calidad para las líneas de video, sin ninguna de las molestas discontinuidades encontradas en las líneas de audio. Tales discontinuidades en la respuesta en frecuencia son ocasionalmente causadas por el hábito de las compañías de telecomunicaciones de formar una conexión al unir dos líneas más cortas y de diferente impedancia característica. Las líneas de vídeo, por el contrario, tienden a decaer suavemente con la frecuencia en una manera predecible.

Tal respuesta más predecible del vídeo permite técnicas de diseño diferentes. El ecualizador de vídeo es construido como una sola sección de puente T pero con una más compleja red para Z. Para líneas cortas, o para un ecualizador de recorte, una topología de filtro de Bode puede ser usada. Para líneas más largas una red con topología de filtro Cauer puede también ser usada. Otro controlador para tal técnica es el hecho de que la señal de vídeo ocupará un largo número de octavas (alrededor de 20). Si se es ecualizada con secciones simples, un amplio número de secciones de filtrado serían requeridas. Las secciones simples son diseñadas, típicamente, para ecualizar un rango de una o dos octavas.

Ecualizador de Bode

Una red Bode, tal y como con la Zobel, es un puente simétrico de red T, que cumple con la condición de k constante. Sin embargo, no cumple con la condición de resistencia constante, es decir, el puente no está en balance.[4]​ Cualquier red con impedancia, Z, puede ser usada en una red Bode, justo como con la red Zobel, pero la sección pasa altas mostrada para corregir las frecuencias de alto término es la más común. Una red Bode terminada en una resistencia variable puede ser usada para producir una impedancia variable en las terminales de entrada de la red. Una propiedad útil de esta red es que la impedancia de entrada puede ser hecha para variar de una impedancia capacitiva hacia una resistencia puramente resistiva o una impedancia inductiva, todo con el ajuste de un potenciómetro. La resistencia de puenteo R₀, es escogida para igualar la impedancia nominal para que en el caso especial cuando R_L es puesta a R₀ la red se comporte como una red Zobel y Z_in se también sea igual a R₀.

Respuesta de un ecualizador de corte Bode

La red Bode se usa en un ecualizador al conectar la red completa de tal manera que la impedancia de entrada de la misma Z_in, esté en serie con la carga. Dado que la impedancia de la red de Bode puede ser capacitiva o inductiva dependiendo en la posición del potenciómetro, la respuesta puede ser un empuje o un corte a la banda de frecuencias sobre las que actúa. La función de transferencia del arreglo es:

${\displaystyle A(\omega )={\frac {R_{0}}{Z_{in}+R_{0}}}}$

El ecualizador de Bode puede ser convertido en un filtro de resistencia constante al usar la red de Bode entera como la rama Z de una red Zobel, resultando en una red de puente T compleja embebida en un puente T más grande. Puede ser visto que esto resulta en la misma función de transferencia al notar que la función de transferencia del ecualizador de Bode es idéntico a la función de transferencia de la forma general del ecualizador Zobel. Nótese que el dual de un puente T de resistencia constante es la red idéntica. El dual de la red de Bode es por lo tanto la misma red excepto por la resistencia de carga R_L, que debe ser la inversa, R_L', en el circuito dual. Para ajustar la R_L y R_L' del ecualizador, estas deben ser ajustadas, o de otra manera, mantenidas de tal modo que cuando R_L incremente, R_L' disminuya y viceversa.

Ecualizador Cauer

Para ecualizar líneas de vídeo largas, una red con topología Cauer es usada como la impedancia Z de una red Zobel de resistencia constante. Para esto la impedancia de entrada de una red de Bode es usada para la impedancia Z de una red Zobel para formar un ecualizador Zobel Bode. El ecualizador es requerido para corregir una atenuación que incrementa con las frecuencias. Para esto la red en escalera Cauer consiste de resistencias en serie y capacitores desviados. Opcionalmente, puede haber un inductor incluido en serie con el primer capacitor que incremente la ecualización en la última parte. Esto a su vez es requerido en líneas más largas. La resistencia desviada R₁ proporciona la pérdida básica de la red Zobel en el modo usual.

El dual de una red RC de Cauer es una red LR que es requerida para la impedancia Z' como se muestra en el ejemplo. El ajuste resulta un tanto problemático con tal ecualizador. Para mantener la resistencia constante, los pares de componentes C₁/L₁', C₂/L₂' etc., deben permanecer como impedancias duales cuando el componente es ajustado. Con el ecualizador Zobel Bode, esto es un simple arreglo al poner 2 potenciómetros juntos – una configuración de componentes que se puede comprar. Poner juntos un capacitor variable y un inductor, no es una solución muy práctica. Tales ecualizadores tienden a ser construidos a mano, una solución siendo el seleccionar los capacitores en pruebas de acuerdo a las mediciones y después ajustar los inductores hasta que se obtiene el acoplamiento deseado. En tales casos, el elemento más alejado de la escalera se encuentra ecualizando la frecuencias más baja de interés. Esto es ajustado al inicio dado que también tendrá un efecto en frecuencias más altas y de ahí frecuencias progresivamente más altas son ajustadas trabajando conforme a la escalera se acerca al punto de control.

Referencias

1. Zobel, O. J., Theory and Design of Uniform and Composite Electric Wave Filters, Bell Systems Technical Journal, Vol. 2 (1923), pp. 146.
2. Farago, PS, An Introduction to Linear Network Analysis, The English Universities Press Ltd, 1961, pp117-121.
3. Leach, W. M., Jr., Impedance Compensation Networks for the Lossy Voice-Coil Inductance of Loudspeaker Drivers, Georgia Institute of Technology, School of Electrical and Computer Engineering, J. Audio Eng. Soc., Vol. 52, No. 4, April 2004. Available on-line here [1]
4. Bode, Hendrik W., Wave Filter, US patent 2 002 216,, filed 7 June 1933, issued 21 May 1935.

• Zobel, O. J., Distortion correction in electrical circuits with constant resistance recurrent networks, Bell Systems Technical Journal, Vol. 7 (1928), p. 438.
• Redifon Radio Diary, 1970, William Collins Sons & Co, 1969

• Datos: Q3933697
• Multimedia: Zobel networks / Q3933697