Par cinemático

Algunos tipos de uniones entre piezas

En ingeniería mecánica se denomina par cinemático a una unión entre dos miembros de un mecanismo. Un ejemplo son dos barras unidas por un perno (llamado unión de revoluta) que permite que las piezas giren alrededor de él.[1]​

Los pares cinemáticos se clasifican en distintos tipos según el movimiento que permiten, y son un elemento primordial en la construcción de un mecanismo, dado que define el tipo de movimiento que habrá entre las piezas unidas[2]​.

El ingeniero alemán Franz Reuleaux definió el par cinemático como un nuevo elemento en el estudio de las máquinas[3]​ que representaba un avance con respecto a los elementos cinemáticos consistentes de máquinas simples.[4]​

Tipos de pares cinemáticos

En dos dimensiones

Para mecanismos planos, es decir, que ejecutan un movimiento en el plano, algunos ejemplos de pares cinemáticos son[1]​:

• La articulación, que elimina el desplazamiento de traslación relativo de dos sólidos obligando permanentemente a que dos puntos geométricos de los dos sólidos ocupen continuamente la misma posición. Sin embargo, la articulación no impide la reorientación o giro relativo de un sólido respecto al otro.
• La guía corredera, que elimina un grado de libertad de traslación y la posibilidad de reorientación de un sólido respecto a otro.

En tres dimensiones

Más en general se tiene[1]​:

• La articulación cilíndrica, que elimina todos los grados de libertad excepto la posibilidad de rotación de un sólido respecto al otro alrededor de un cierto eje de giro, elimina cinco grados de libertad.
• La rótula esférica, que permite cualquier giro o cambio de orientación de un sólido respecto a otro, pero impide su traslación relativa, por lo que siempre un punto geométrico de ambos sólidos es común, elimina tres grados de libertad.
• Guía deslizante cilíndrica, permite la traslación relativa y el giro alrededor de un eje, elimina por tanto cuatro grados de libertad.
• Guía deslizante no cilíndrica, permite la traslación relativa según un eje pero no el giro alrededor del mismo, elimina por tanto cinco grados de libertad.
• La soldadura elimina todos los grados de libertad de un sólido respecto a otro, por lo que dos sólidos soldados cinemáticamente pueden considerarse un único sólido, es decir, elimina seis grados de libertad.

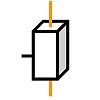
Rodamiento

Una conexión articulada se denomina apoyo si uno de los dos cuerpos está firmemente conectado a la estructura de la máquina o a la cimentación y, por lo tanto, está en reposo.[2]​ A diferencia de una articulación, un rodamiento no suele formar parte de un mecanismo más complejo (engranaje). En el primer plano de su consideración está casi siempre sólo el único tipo de conexión móvil que tiene lugar en él. Los semiejes giratorios y los cuerpos desplazables linealmente (rodamientos lineales) se montan en máquinas y dispositivos, vigas de puentes en la industria de la construcción u otras estructuras soportadas puntuales. En los aparatos de apoyo en estructuras, a diferencia de los de máquinas y dispositivos, solo se producen movimientos muy pequeños (cambios y rotaciones). Solo sirven para crear rodamientos determinados estáticamente y para mantenerlos en caso de perturbaciones (hundimiento, cambios de longitud relacionados con la temperatura, etc.).[2]​

En lugar de cojinetes lisos, los rodamientos de rodillos con elementos rodantes insertados entre los elementos de unión se utilizan a menudo como cojinetes en máquinas y dispositivos. Estos también corresponden a las formas básicas de las juntas juntas giratorias y de corte, mientras que las llamadas "juntas rodantes" utilizadas en la construcción como cojinetes en su forma básica juntas curvas (cuando se empareja hormigón con hormigón, sólo es posible rodar).[5]​

Elementos de máquinas

Junta universal

Montaje cardánico de la brújula de un barco. El anillo más externo está firmemente unido al barco. Las extensiones en forma de cojinete del círculo exterior son una indicación de la cabeceo del barco; de lo contrario, son verticales.

Articulación cardánica como elemento de máquina para conexión a dos ejes contrarrotativos.
El adaptador, junto con los pivotes, tiene forma de cruz.
Los ejes de todas las articulaciones se encuentran en un punto. La caja de engranajes de cuatro partes obtenida con las juntas de cojinete del eje (no mostradas) y el bastidor de la máquina es esférico).

La junta universal o cardán es una serie de dos juntas rotativas. La segunda superficie de contacto de cada una de las dos juntas se encuentra en la pieza intermedia común en forma de cruz (ver figura de la derecha). Los ejes de las juntas giratorias se cortan a 90°. El punto de intersección es el punto de pivote en el que los dos "vástagos" de articulación dispuestos en ángulo recto con respecto al eje de articulación de pivote respectivo pueden pivotar entre sí. La articulación cardánica tiene dos grados de libertad de movimiento. En comparación con la rótula, carece de la libertad de rotación de los vástagos de la articulación alrededor de su propio eje. Su grado de libertad es f=2.[2]​

La aplicación históricamente más antigua fue el cardán, en el que es posible el pivote sobre los dos ejes espaciales horizontales, pero no se permite la rotación sobre el eje vertical. La pieza intermedia es un anillo.

La falta de libertad de rotación alrededor de los vástagos de la junta también hace que la junta universal sea adecuada para la transmisión de par entre ejes que pueden pivotar uno contra otro (eje cardán).

Juntas de velocidad constante

Al igual que la junta universal, las juntas homocinéticas se utilizan para la transmisión de par entre ejes que pueden girar en direcciones opuestas. No tienen el inconveniente de no ser completamente sincrónicos, sino que fluctúan periódicamente con la rotación. Al igual que la junta universal, son rótulas reducidas a dos movimientos giratorios en el exterior. En el interior, al igual que en la junta universal, también hay piezas intermedias cuyos elementos de unión están en contacto con superficies de bolas o casquillos variados. En el caso de la "junta Rzeppa", por ejemplo, las bolas están en contacto con superficies esféricas acanaladas.

Articulaciones elásticas en ingeniería mecánica

Las juntas de resorte no pertenecen a las formas básicas de juntas ni a los campos en los que los cuerpos rígidos se deslizan y/o ruedan unos sobre otros. Están disponibles como juntas giratorias y deslizantes aproximadas con poca movilidad. Un cuerpo que cede elásticamente, por ejemplo una varilla de resorte que está torcida o doblada, instalada permanentemente. Las juntas de resorte tienen la ventaja de estar libres de fricción, juego y mantenimiento.[6]​

Las juntas de resorte de torsión se usan a menudo en instrumentos de medición mecánicos, donde el momento de torsión se puede usar como un momento de restauración.

Si la junta de resorte no se realiza con un componente separado sino con un debilitamiento local del propio componente, esto se denomina junta de flexión.

Articulación de dirección

Conexión deslizante

La conexión deslizante modela un contacto cilíndrico que no es de revolución (es decir, generado por traslación)[1]​.

La conexión deslizante proporciona cinco grados de conexión al permitir únicamente el movimiento de traslación en la dirección de la conexión. La definición de esta conexión debe especificar esta dirección.

Existen varios enfoques posibles para realizar esta conexión[1]​:

• a partir de un soporte plano (3 grados de conexión): se añade un segundo plano de contacto, secante con el primero o, más sencillamente, un eje guía lateral (conexión lineal recta) paralelo al plano ;
• a partir de una conexión pivotante deslizante (4 grados de conexión): basta con una conexión puntual que impida la rotación, lo que se denomina "antigiro" (generalmente 2 puntos opuestos).

A un nivel más tecnológico, se puede considerar el carácter bilateral de esta conexión. Por ejemplo, los cajones de una cómoda están guiados bilateralmente, mientras que la vía del ferrocarril ofrece una conexión unilateral en sentido vertical.

Esta es la conexión proporcionada en una transmisión por eje. Ranura que modela el guiado de la corredera de un trombón o el pistón de una trompeta.[2]​

A diferencia del movimiento de rotación del eslabón pivotante, la amplitud de la traslación posible está limitada por las dimensiones de las piezas. Cuando el cajón está totalmente extendido, ¡el eslabón ya no existe! La modelización matemática no tiene en cuenta los límites de la guía.[2]​

• 
  La solución más obvia pero no por ello menos hiperestática.
• 
  La corredera de un trombón está unida al cuerpo del instrumento por una corredera, combinando dos pivotes deslizantes con ejes paralelos (solución hiperestática).
• 
  Conexión cola de milano para una conexión bilateral.
• 
  5 puntos = deslizamiento

Deslizamiento de dirección X				Uniones : Ty = 0 Tz = 0 Rx = 0 Ry = 0 Rz = 0	Libertad : Tx

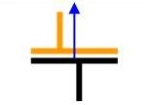
Cuando dos sólidos están en una conexión deslizante, hay al menos dos líneas estrictamente paralelas comunes a ambos sólidos, cuya dirección define la única característica geométrica de la conexión.

Por error, a esta conexión se le asigna un eje. Si bien es cierto que las soluciones utilizadas para realizar esta conexión suelen incluir planos o ejes de simetría, su definición geométrica no los necesita.

Dado que la movilidad de los objetos no puede compararse a la de los objetos colocados en una pista de patinaje que permite un deslizamiento casi ideal, las consideraciones menos teóricas de enlaces mecánicos con rozamiento conducen al atasco por arco-boutement. Esto demuestra que la disposición de la carga con respecto a las superficies de contacto influye (tribología).

Conexión plana o plano/plano

La conexión plana (a veces llamada incorrectamente conexión plana de apoyo, que es un término utilizado para describir el contacto) tiene 3 grados de conexión. Obligan al movimiento a permanecer en un plano. Las dos traslaciones y la rotación en este plano son libres.

Esta conexión se obtiene naturalmente presionando dos superficies planas una contra otra. De forma más general, basta con que el contacto entre dos sólidos se produzca en al menos 3 puntos no alineados con normales en la misma dirección. Esta es la base de los llamados enlaces prismáticos. La dirección común de las normales de los contactos elementales da la "dirección principal de la unión".

El apoyo de las tres patas de un taburete sobre un suelo plano constituye una conexión plana. La cuarta pata de una silla sólo toca el suelo si los extremos de las patas son perfectamente coplanarios; el sistema es entonces hiperestático los enlaces superan en número a la necesidad de guía.

• 
  Dos caras planas en apoyo.
• 
  Ejemplos de soportes planos
• 
  Un taburete de tres patas nunca se tambalea: solución isostática.
• 
  3 puntos = soporte plano

Apoyo plano de normal Z		no normalizado		Enlaces : Tz = 0 Rx = 0 Ry = 0	Libertad : Tx, Ty Rz

Los puntos de contacto no están necesariamente en el mismo plano. Por ejemplo, si acorta una pata de una silla, puede colocarla en una escalera, con la pata más corta apoyada en un escalón superior. Como las normales son paralelas, el conjunto es siempre una conexión plana.

Cuando dos sólidos están en contacto plano, al menos un plano de uno de ellos coincide con un plano del otro.

Conexiones de ejes

Unión pivotante

La unión pivotante es el tipo de conexión más utilizado en los sistemas mecánicos. Guía una pieza en rotación permitiendo un único giro alrededor del eje de la conexión[1]​.

La definición de esta unión debe especificar "la posición de su eje", es decir, una línea recta como en el caso de un pivote deslizante. En el caso de una puerta, la posición de las bisagras determina el sentido de su apertura; del mismo modo, el portón trasero de un coche está guiado por un pivote horizontal situado en la parte superior. Si estuviera en la parte inferior, el resultado sería una puerta forzada. Por tanto, la precisión de la dirección por sí sola es insuficiente.

Los diseños más habituales se basan en completar un contacto cilíndrico con un tope axial: a menudo se trata de un plano normal al eje (pivote deslizante + apoyo plano: solución hiperestática); en este caso, se distingue entre pivotes con predominio cilíndrico (en el caso de una rueda unida por un cojinete liso como en una carretilla) o plano (en el caso de una tapa). Lo ideal es combinar un pivote deslizante con una conexión puntual.[2]​

Esta unión también puede obtenerse combinando una unión lineal anular y una rótula; un esquema que se encuentra en ciertas guías de rodamiento de bolas con tope sobre un cojinete.

En el caso de las uniones pivotantes, sobre todo en lo que respecta al bloqueo de la traslación axial, se distingue entre uniones unilaterales y bilaterales, según se elimine este grado de libertad en uno o en ambos sentidos. Si para una puerta la solución unilateral[7]​ es suficiente, es necesario sujetar la rueda de un vehículo en ambos sentidos. Este enfoque es, por supuesto, tecnológico y no se refiere a este asunto.[2]​

• 
  Conexión pivote por cilindro y plano radial (solución hiperestática y unilateral)
• 
  Soluciones constructivas bilaterales para unir llaves de un instrumento musical
• 
  El pedal está unido a su muñequilla por cojinetes siguiendo una conexión de pivote
• 
  5 puntos = pivote

Pivot d'axe (A,Z)				Uniones : Tx = 0 Ty = 0 Tz = 0 Rx = 0 Ry = 0	Libertad : Rz

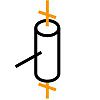
Sin embargo, es posible obtener una conexión pivotante mediante un simple contacto, dos conos complementarios o dos superficies de revolución de sección reducida. Esta conexión se considera compuesta, porque las superficies consideradas aquí no tienen la forma totalmente banal del cilindro simple.

Cuando dos sólidos están unidos pivotantemente, hay al menos 2 puntos fijos coincidentes en cada sólido. La recta que pasa por estos puntos constituye el eje de la unión.

Unión pivotante deslizante o cilindro/cilindro

La unión pivotante deslizante modela un contacto cilíndrico de revolución[1]​.

Se obtiene cuando todos los puntos de contacto pertenecen a uno o varios cilindros coaxiales. Todas las normales de contacto coinciden con el eje de estos cilindros, que se convierte naturalmente en el eje de la conexión. Ésta es la única dirección característica.

Las cajas de cambio del 2CV y del 4L están unidas al salpicadero por un pivote deslizante.

Este eslabón se comporta como dos eslabones lineales anulares. Tiene 4 grados de libertad ya que une las dos traslaciones y las dos rotaciones transversales. Los grados de libertad son la traslación y la rotación axial.

Si la rotación puede tener fácilmente una amplitud infinita (al menos una revolución), la traslación se limita a las dimensiones de las piezas. Sin embargo, en el dominio operativo observado, el modelado se mantiene.

La definición completa de este enlace debe especificar la posición del eje. Como es una línea recta, sólo es completa si se especifican 2 puntos que le pertenecen, o un punto y una dirección. Esta dirección es también la única que se destaca.

• 
  Solución para un pivote deslizante.
• 
  Las filas de jugadores en miniaturas de un futbolín están unidas a la mesa por un pivote deslizante.
• 
  4 puntos = pivote deslizante

Pivote deslizante d'axe (A,x)				Liaisons : Ty = 0 Tz = 0 Ry = 0 Rz = 0	Libertés : Tx Rx

A diferencia de la conexión anular lineal, ésta requiere un centrado largo. La distinción tecnológica entre ambas se basa en la relación entre el radio y la longitud de vano (ensamblaje cilíndrico):

• si L < R, se aceptará el modelo anular. La holgura permite una gran desviación angular;
• si L > 2R, se requiere el modelo de pivote deslizante. El mismo juego radial hace despreciable la desviación angular ;
• entre los dos, corresponde al mecánico hacer una elección, que estará motivada por los resultados esperados. En el caso de un estudio estático, se prefiere el modelo menos restrictivo y con menos incógnitas. En el caso de un estudio cinemático, se prefiere el eslabón más restrictivo, que proporciona más ecuaciones para resolver el problema.

Este eslabón es muy común en mecanismos, donde a veces se confunde con el eslabón deslizante. Sin embargo, es menos restrictivo de crear. Algunos ejemplos son la conexión entre pistón y camisa, y, aún en el motor de explosión, entre pistón y biela (aunque, también en este caso, pueda parecer una conexión pivotante). En ambos casos, la elección de una conexión menos constreñida permite posicionar las piezas de forma natural.

Conexión helicoidal

El deslizamiento de un eje estriado se modela mediante una conexión deslizante. Si enrollamos las estrías alrededor del eje, nos encontramos en presencia de un tornillo en su tuerca. Esto se conoce como conexión helicoidal.

Lo que caracteriza a esta conexión es la existencia de un movimiento "combinado": la rotación es simultánea a la traslación en una relación denominada paso de tornillo, hélice o rosca. Se trata, por tanto, de un único grado de libertad.

La conexión tiene, por tanto, 5 grados de conexión, incluyendo 2 traslaciones y 2 rotaciones transversales. El otro se debe al acoplamiento de la traslación axial y la rotación mediante una relación helicoidal del tipo x = u-θx. El paso del enlace p = 2π-u indica la longitud recorrida en una revolución (2π radianes).

La definición de este enlace debe especificar la posición de su eje, la dirección de la hélice y el valor del paso.

La consideración de esta conexión es esencial en el estudio de los dispositivos de tornillo-tuerca, cuya finalidad es transformar el movimiento de rotación en movimiento de traslación. En cambio, el estudio de un conjunto que utilice pernos o tornillos no requiere esta modelización. Existen husillos a bolas (asociados a su tuerca) diseñados para transmitir el movimiento, y que ofrecen una excelente eficacia.

La dirección de la hélice, a menudo hacia la derecha, puede invertirse. El antiguo esquema (todavía válido) propuesto aquí permite (a diferencia del nuevo) distinguir entre los dos casos.

• 
  Un tornillo y varias tuercas
• 
  La tuerca y el husillo de bolas son, para el helicoidal, el equivalente del rodamiento.
• 
  5 puntos = helicoidal
• 
  Piezas de conexión por tornillo y tuerca.

Helicoidal en el eje (A,X) y de paso p				Uniones : x = u·θx Ty = 0 Tz = 0 Ry = 0 Rz = 0	Libertad : ${\displaystyle {\begin{pmatrix}u.\theta _{x}\\0\\0\\\theta _{x}\\0\\0\end{pmatrix}}}$

Conexión cilindro/plano

Esta conexión se obtiene cuando presenta un conjunto de puntos de contacto alineados cuyas normales están todas en el mismo plano. Lo ideal es la asociación de 2 puntos.

Existen 2 grados de conexión: la traslación perpendicular al plano tangente (es decir, en la dirección de las normales) y cualquier rotación con un eje perpendicular al plano de las normales de contacto.

A pesar de su simplicidad, esta conexión es sin duda la más tridimensional de todas, ya que su comportamiento es diferente en las 3 direcciones del espacio. Por lo tanto, su definición completa debe especificar el plano que contiene la dirección de la línea de puntos de contacto y la dirección común de las normales de contacto.

Como en el caso del contacto puntual, el contacto a lo largo de una línea (de espesor nulo) es improbable. Se produce deformación bajo presión. Una superficie rectangular de poca anchura puede considerarse una línea de contacto: un rodillo sobre su soporte o una placa colocada sobre un borde delgado son casos de contacto lineal rectilíneo.

También en este caso, el resultado suele ser una conexión unilateral real. Sin embargo, un pasador ajustado que se desliza en una ranura oblonga es una solución bilateral. Las dos líneas de contacto son paralelas y se encuentran en un plano que también contiene el conjunto de las normales de contacto.

• 
  Conexión lineal rectilínea por cilindro colocado en un plano
• 
  2 puntos = rectilínea
• 
  En un engranaje recto[8]​, el enlace entre dos ruedas puede modelizarse mediante un rectilíneo lineal si el espesor de los piñones no es despreciable.
• 
  Solución bilateral.

Lineal rectilínea d'axe (A,x) y de normal Z				Uniones : Tz = Z Ry = M	Libertad : Tx, Ty Rx, Rz

Cuando dos partes están unidas por una línea recta, hay dos puntos fijos de una de las partes que coinciden con una superficie fija de la otra.

Referencias

1. R. C. Stephens, John Hannah. Mechanics Machines: Elementary Theory & Examples. (1984) 312 pag. , ISBN 0713134712, ISBN 978-0713134711
2. Robert L. Mott. Machine Elements in Mechanical Design (2019) ISBN 9353947634, ISBN 978-9353947637
3. Reuleaux, F., 1876 The Kinematics of Machinery, (trans. and annotated by A. B. W. Kennedy), reprinted by Dover, New York (1963)
4. A. P. Usher, 1929, A History of Mechanical Inventions, Harvard University Press, (reprinted by Dover Publications 1968).
5. Steffen Marx, Gregor Schacht: Juntas en construcción sólida
6. Siegfried Hildebrand. Fertigungsgerechtes Gestalten in der Feinwerktechnik: Fertigungsverfahren, Werkstoffe, Konstruktionen (1978) 272 pag. ISBN 3528040858, ISBN 978-3528040857
7. Para las puertas más comunes, la bisagra solo mantiene la puerta hacia abajo. Entonces solo levanta la puerta para desquiciar.
8. Esta modelización sólo es relevante para el estudio en profundidad del comportamiento de un engranaje. La consideración del engranaje ha de tomarse a un nivel mucho más macroscópico (ver apartado Otras uniones cinemáticas).

Bibliografía

• Feynman, Richard (1999). Lectures on Physics. Perseus Publishing. ISBN 978-0-7382-0092-7.
• Landau, L. D.; Lifshitz, E. M. (1972). Mechanics Course of Theoretical Physics , Vol. 1. Franklin Book Company. ISBN 978-0-08-016739-8.
• Eisberg, Robert Martin (1961). Fundamentals of Modern Physics. John Wiley and Sons.

Véase también

• Mecanismo
• Grados de libertad (ingeniería)

• Datos: Q526016
• Multimedia: Kinematic pairs / Q526016