|
Mecánica molecular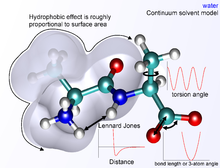 La mecánica molecular es una técnica de simulación que utiliza la mecánica clásica para emular sistemas moleculares. Este método asume la aproximación de Born-Oppenheimer como válida y la energía potencial de todos los sistemas es calculada como una función de las coordenadas nucleares utilizando campos de fuerza. La mecánica molecular puede ser utilizada para estudiar sistemas moleculares que varían en tamaño y complejidad, desde moléculas orgánicas pequeñas, hasta sistemas biológicos complejos (proteínas, polisacáridos, ácidos nucléicos), o materiales que contienen miles de millones de átomos.[1][2] Los métodos de mecánica molecular completamente atomísticos tienen las siguientes propiedades:
Las variantes en este tema son posibles, por ejemplo, diversas simulaciones han utilizado representaciones united-atom (átomos unidos), en los que cada grupo terminal metilo o intermediarios metileno, eran considerados una partícula única; y sistemas proteicos grandes, usualmente son representados utilizando un modelo de perlas que asigna de dos a cuatro partículas por cada aminoácido. En este contexto, la palabra partícula, se refiere a una unidad de cálculo dentro de la representación establecida y no necesariamente corresponde a un átomo o a un monómero, en el caso de los sistemas poliméricos. Forma de la función E(R)El siguiente funcional, nombrado función del potencial interatómico, o campo de fuerza en química, calcula la energía potencial del sistema molecular (E) en una conformación dada como la suma de los términos individuales de energía:
Donde los componentes de cada contribución se dan por las siguientes sumas:
La forma exacta del funcional depende del programa de simulación que se esté utilizando. Por lo general, los términos de enlace y ángulo se modelan como potenciales armónicos centrados en valores de la longitud de enlace al equilibrio derivados de experimentos o cálculos teóricos de la estructura electrónica (usualmente realizados con software de cálculos ab-initio como Gaussian). Para una reproducción precisa del espectro vibracional, el potencial de Morse puede utilizarse en su lugar, con un costo computacional mayor. el término diedro, o de torsión, típicamente posee múltiples mínimos y no puede ser modelado como un oscilador armónico, por lo que su funcional varía con cada implementación. Esta clase de términos pueden incluir términos diedro impropios, que funcionan como factores de corrección para desviaciones fuera del plano (por ejemplo, pueden utilizarse para mantener anillos de benceno planos o corregir la geometría y quiralidad de átomos tetraédricos). Los términos no enlazantes, o no covalentes, son mucho más costos computacionalmente para calcular de manera completa. Esto se debe a que un átomo está enlazado únicamente a unos cuantos vecinos mientras que interactúa con cada uno de los átomos en la molécula. Afortunadamente, el término de van der Waals decae rápidamente. Se modela normalmente utilizando un potencial de Lennard-Jones 6-12, que significa que las fuerzas atractivas decaen con la distancia con un factor de r -6 mientras que las fuerzas repulsivas lo hacen un factor de r -12, donde r representa la distancia entre los átomos. La parte repulsiva no tiene interpretación física, pues la repulsión se incrementa exponencialmente. La descripción de las fuerzas de van der Waals según el potencial de Lennard-Jones genera inexactitud, la cual se vuelve relevante a distancias cortas.[3] Generalmente, un radio de corte es utilizado para acelerar los cálculos, de manera que los pares atómicos cuyas distancias sean mayores que el corte, automáticamente consideren una energía de interacción de van der Waals de cero. Los términos electrostáticos son notoriamente difíciles de calcular correctamente debido a que no decaen rápidamente con la distancia y las interacciones a larga distancia normalmente son características importantes en los sistemas de estudio, especialmente proteínas. La forma básica del funcional es el potencial coulómbico, que sólo decae con el término r-1. Una variedad de métodos son utilizados para aproximarse al problema, siendo la más simple un radio de corte similar al usado en los términos de van der Waals. Sin embargo, esto introduce una discontinuidad marcada entre los átomos dentro y fuera del radio. Cambiar o escalar funciones que modulan la energía electrostática aparente son métodos más precisos que multiplican la energía calculada por una escala que varía ligeramente de 0 a 1 fuera y dentro del radio. Otros métodos más sofisticados pero computacionalmente intensivos son la malla de partículas de Ewald (particle mesh Ewald, PME) y el algoritmo multipolar. Además de la forma del funcional para cada término, una función de energía debe ser alimentada por parámetros de constantes de fuerza, multiplicadores de van der Waals y otros términos constantes. Estos términos, junto con los valores de enlace, ángulo y diedro al equilibrio, así como cargas parciales, masas atómicas, radios y definiciones para las funciones de energía, se nombran colectivamente campo de fuerza. La parametrización de realiza típicamente a través de la coincidencia de valores experimentales y calculados. Cada campo de fuerza es parametrizado para ser internamente consistente, pero los parámetros generalmente no son transferibles de un campo a otro. Áreas de aplicaciónEl uso principal de la mecánica molecular es en el campo de la dinámica molecular. Éste utiliza un campo de fuerza para calcular las fuerzas que actúan en cada partícula y un integrador adecuado para modelar la dinámica de las partículas y predecir trayectorias. Con suficientes muestreos y siguiendo la hipótesis de ergodicidad, las trayectorias de la dinámica molecular pueden ser utilizadas para estimar los parámetros termodinámicos en un sistema de propiedades cinéticas dadas, como velocidades de reacción y mecanismos. Otra aplicación de mecánica molecular es la minimización de la energía, donde los campos de fuerza se utilizan como criterios de optimización. Este método utiliza un algoritmo apropiado para encontrar la estructura molecular que conlleve al mínimo local de energía. Este mínimo corresponde al confórmero estable de la molécula y un movimiento de ésta puede ser modelado como vibraciones e interconversiones entre estos confórmeros estables. Por lo tanto, es común encontrar métodos de minimización local de la energía combinados con optimizaciones globales de energía para encontrar el mínimo global de energía. A una temperatura finita, esta molécula gasta la mayoría de su tiempo en estos estados de baja energía, por lo que dominan las propiedades moleculares. La optimización global puede ser lograda a través de cristalización simulada, algoritmo de Metrópolis y método de Montecarlo, o utilizando diferentes métodos deterministas de optimización discreta o continua. Mientras que el campo de fuerza representa sólo el componente entálpico de la energía libre, es posible incluir el componente entrópico a través de métodos adicionales como el análisis del modo normal. Las funciones de energía potencial de la mecánica molecular han sido utilizadas para calcular constantes de formación,[4][5][6][7][8] cinética de plegamiento de proteínas,[9] equilibrios de protonación,[10] sitios activos de coordinación[6][11] y para diseñar sitios de enlace.[12] Ambiente y solvataciónEn mecánica molecular, existen diferentes formas de definir el entorno de una molécula de interés. Un sistema puede ser simulado en un vacío, pero esto usualmente es poco deseable debido a que introduce cambios en la geometría molecular, especialmente de moléculas cargadas. Los cambios en la superficie que podrían interactuar de forma normal con las moléculas del solvente, en un vacío interactúan con ellos mismos, produciendo conformaciones improbables en cualquier otro entorno. La mejor manera de solvatar un sistema es colocar explícitamente moléculas de agua en la caja de simulación con las moléculas de interés y tratar a estas moléculas de agua como partículas que interactúan de la misma forma que la molécula. Una variedad de modelos de agua existen con diferentes niveles de complejidad, representando al agua como una simple esfera sólida, como 3 partículas separadas con ángulos de enlace fijos o incluso como 4 o 5 centros de interacción separados, para tomar en cuenta a los pares electrónicos libres en el átomo de oxígeno. Por supuesto, mientras más complejo sea el modelo del agua, más demandante será la simulación. Un método de solvatación implícita se ha desarrollado, en el que se reemplazan las moléculas de agua representadas explícitamente por una expresión matemática que reproduce el comportamiento promedio de las moléculas de agua (o de otros solventes). Este método es útil para prevenir problemas que surgen de simulaciones en el vacío y reproduce correctamente propiedades masivas del solvente, pero es incapaz de reproducir situaciones en las que moléculas individuales de agua poseen interacciones relevantes con las moléculas de estudio. Paquetes de software
Referencias
|
Portal di Ensiklopedia Dunia


