|
Lente tórica Una lente tórica es una lente con diferente potencia óptica y longitud focal en dos orientaciones perpendiculares entre sí. Una de las superficies de la lente se forma como superficie "límite" de un toro de revolución (véase el gráfico de la derecha), mientras que la otra es en general esférica. Las lentes tóricas se utilizan principalmente en gafas, lentes de contacto o en una lente intraocular, para corregir el astigmatismo.[1][2] Toro de revolución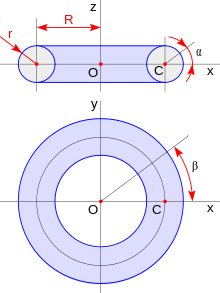 Un toro es el cuerpo espacial que resulta cuando un círculo con radio r gira alrededor de un eje situado en el mismo plano que el círculo, a una distancia R del centro del círculo (figura de la derecha). Si R > r , se produce un toro de anillo . Si R = r , se produce un toro de cuerno , cuando la apertura se contrae en un solo punto. R < r resulta un toro axial , donde sólo quedan dos "dips" de la apertura, estos "dips" son menos profundos a medida que R acerca a 0. Cuando R = 0, el toro degenera en una esfera con radio r .[3]  [1]
Lente tóricaEl radio mayor de curvatura de la superficie de la lente tórica, R + r, corresponde a la menor potencia refractiva, S = (n − 1) / (R + r), donde n es el índice de refracción del material de la lente. El radio menor de curvatura, r , se corresponde con la mayor potencia de refracción, s = (n − 1) / r, ya que R + r > r, S < s. La lente se comporta aproximadamente como una combinación de una lente esférica con una potencia óptica s y una lente cilíndrica con una potencia óptica s − S. En oftalmología y optometría, a s − S se le llama "potencia cilíndrica" de la lente, y se utiliza para corregir el astigmatismo. En este contexto, el término "cilindro se basa en una aproximación matemática, que sólo es válida para las pequeñas potencias correctivas.[4] Hay que tener en cuenta que tanto la curvatura mayor como la menor tienen una sección circular, por lo tanto, en contra de lo que se podría pensar, la lente tórica no es en absoluto un elipsoide de revolución. FuncionamientoLos rayos de luz dentro del plano (x,y)- del toro (como se define en la figura anterior) son refractados de acuerdo con el radio de curvatura grande, R + r, es decir, con la menor potencia de refracción,S = (n − 1) / (R + r). Los rayos de luz dentro de un plano a través del eje de revolución (el eje z ) del toro se refractan de acuerdo con el radio de curvatura pequeño, r , es decir, la mayor potencia de refracción,s = (n − 1) / r. Como consecuencia, hay dos grados de refracción diferentes en orientaciones perpendiculares entre sí. En orientaciones intermedias, los cambios de potencia de refracción varían de forma gradual desde el valor más grande hasta el valor más pequeño, o al revés. Esto se hace para compensar la aberración astigmática del ojo. Lente atóricaCon las técnicas modernas de diseño, esmerilado y pulido, controlados por ordenador, se pueden conseguir lentes con buenas correcciones de graduación incluso para amplios ángulos de visión, ya que permiten generar pequeñas desviaciones de la forma tórica, este tipo de lente recibe el nombre de lente atórica (literalmente, sin lente tórica).[5] y guarda la misma relación con las lentes tóricas que la que tiene la lente asférica con las lentes esféricas.[6] Véase tambiénReferencias
|
Portal di Ensiklopedia Dunia