Lámina plana

En física, la definición matemática de una lámina plana[1]​ consiste en un conjunto cerrado en un plano de masa ${\displaystyle m}$ y una densidad de superficie ${\displaystyle \rho \ (x,y)}$ tal que:

${\displaystyle m=\int \int _{}{}\rho \ (x,y)\,dx\,dy}$, sobre el conjunto cerrado.

El centro de masas de la lámina está en el punto

${\displaystyle \left({\frac {M_{y}}{m}},{\frac {M_{x}}{m}}\right)}$

donde ${\displaystyle M_{y}}$ es el momento de toda la lámina sobre el eje xy; y ${\displaystyle M_{x}}$ es el momento de toda la lámina sobre el eje y.

${\displaystyle M_{y}=\lim _{m,n\to \infty }\,\sum _{i=1}^{m}\,\sum _{j=1}^{n}\,x{_{ij}}^{*}\,\rho \ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta \mathrm {A} =\iint _{}{}x\,\rho \ (x,y)\,dx\,dy}$, sobre la superficie cerrada.

${\displaystyle M_{x}=\lim _{m,n\to \infty }\,\sum _{i=1}^{m}\,\sum _{j=1}^{n}\,y{_{ij}}^{*}\,\rho \ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta \mathrm {A} =\iint _{}{}y\,\rho \ (x,y)\,dx\,dy}$, sobre la superficie cerrada.

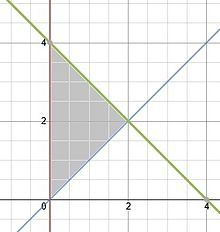
Ejemplo 1. Encuéntrese el centro de masa de una lámina con los bordes dados por las líneas ${\displaystyle x=0,}$ ${\displaystyle y=x}$ y ${\displaystyle y=4-x}$ donde la densidad se da como ${\displaystyle \rho \ (x,y)\,=2x+3y+2}$.

${\displaystyle m=\int _{0}^{2}{\int _{x}^{4-x}}_{}{}\,(2x+3y+2)\,dy\,dx}$

Integrar 2x + 3y + 2 con respecto a y; y sustituir los límites 4-x y x

${\displaystyle m=\int _{0}^{2}\left(2xy+{\frac {3y^{2}}{2}}+2y\right){\Bigg |}_{x}^{4-x}\,dx}$

${\displaystyle m=\int _{0}^{2}\left({\Big [}2x(4-x)+{\frac {3(4-x)^{2}}{2}}+2(4-x){\Big ]}-{\Big [}2x(x)+{\frac {3(x)^{2}}{2}}+2(x){\Big ]}\right)\,dx}$

${\displaystyle m=\int _{0}^{2}\left(8x-2x^{2}+{\frac {3x^{2}-24x+48}{2}}+8-2x-2x^{2}-{\frac {3x^{2}}{2}}-2x\right)\,dx}$

${\displaystyle m=\int _{0}^{2}\left(8x-2x^{2}+{\frac {3}{2}}x^{2}-12x+24+8-2x-2x^{2}-{\frac {3}{2}}x^{2}-2x\right)\,dx}$

${\displaystyle m=\int _{0}^{2}(-4x^{2}-8x+32)\,dx}$

${\displaystyle m=\left(-{\frac {4x^{3}}{3}}-4x^{2}+32x\right){\Bigg |}_{0}^{2}}$

${\displaystyle m={\frac {112}{3}}}$

${\displaystyle M_{y}=\int _{0}^{2}{\int _{x}^{4-x}}{}{}x\,(2x+3y+2)\,dy\,dx}$

${\displaystyle M_{y}=\int _{0}^{2}\left(2x^{2}y+{\frac {3xy^{2}}{2}}+2xy\right){\Bigg |}_{x}^{4-x}\,dx}$

${\displaystyle M_{y}=\int _{0}^{2}(-4x^{3}-8x^{2}+32x)\,dx}$

${\displaystyle M_{y}=\left(-x^{4}-{\frac {8x^{3}}{3}}+16x^{2}\right){\Bigg |}_{0}^{2}}$

${\displaystyle M_{y}={\frac {80}{3}}}$

${\displaystyle M_{x}=\int _{0}^{2}{\int _{x}^{4-x}}{}{}y\,(2x+3y+2)\,dy\,dx}$

${\displaystyle M_{x}=\int _{0}^{2}(xy^{2}+y^{3}+y^{2}){\Big |}_{x}^{4-x}\,dx}$

${\displaystyle M_{x}=\int _{0}^{2}(-2x^{3}+4x^{2}-40x+80)\,dx}$

${\displaystyle M_{x}=\left(-{\frac {x^{4}}{2}}+{\frac {4x^{3}}{3}}-20x^{2}+80x\right){\Bigg |}_{0}^{2}}$

${\displaystyle M_{x}={\frac {248}{3}}}$

el centro de masa está en el punto

${\displaystyle \left({\frac {\frac {80}{3}}{\frac {112}{3}}},{\frac {\frac {248}{3}}{\frac {112}{3}}}\right)=\left({\frac {5}{7}},{\frac {31}{14}}\right)}$

Las láminas planas se pueden usar para determinar momento de inercia, o centros de masa.

Referencias

1. «Lamina». WolframMathWorld (en inglés). Consultado el 21 de abril de 2018. 

• Datos: Q17097792