Icosaedro rómbico

No debe confundirse con el rombicosaedro.
Icosaedro rómbico
Tipo Zonoedro
Caras 20 rombos áureos
congruentes
Aristas 40
Vértices 22
Caras por vértice 3, 4, o 5
Poliedro
conjugado		 Girobicúpula pentagonal
de caras irregulares
Simetría D5d= D5v, [2+,10], (2*5)
Propiedades Convexo, zonoedro

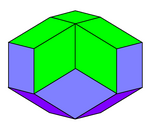
El icosaedro rómbico es un poliedro con una forma similar a la de una esfera achatada. Sus 20 caras son congruentes con el rombo áureo;[1]​ y se unen 3, 4 o 5 caras en cada vértice. Tiene 5 caras (verde en la figura superior) que se encuentran en cada uno de sus 2 polos; estos 2 vértices se encuentran en su eje de simetría pentagonal, que es perpendicular a 5 ejes de doble simetría a través de los puntos medios de las aristas ecuatoriales opuestas (ejemplo en la figura superior: las aristas mediales situadas más a la izquierda y más a la derecha). Sus otras 10 caras se disponen ecuatorialmente (5 por arriba y 5 por debajo de la cintura del poliedro), de manera que cada uno de estos 10 rombos tiene 2 de sus 4 lados sobre este ecuador, formando un decágono alabeado en zig-zag. El icosaedro rómbico tiene 22 vértices, y su grupo de simetría es D5d, [2+,10], (2*5), de orden 20; y por lo tanto, tiene un centro de simetría (ya que 5 es impar).

Aunque todas sus caras son congruentes, el icosaedro rómbico no es una figura isoedral, ya que se puede distinguir si una cara en particular está cerca del ecuador o cerca de un polo examinando los tipos de vértices que rodean esta cara.

Zonoedro

El icosaedro rómbico es un zonoedro, es decir, es dual a una girobicúpula pentagonal con caras triangulares y pentagonales regulares, pero con cuadriláteros irregulares.

El icosaedro rómbico tiene 5 conjuntos de 8 aristas paralelas, descritas como 85 cinturones.

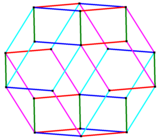
Las aristas del icosaedro rómbico se pueden agrupar en 5 conjuntos paralelos, como se ve en esta proyección ortogonal de su estructura alámbrica.

Es la envolvente convexa de la proyección del primer vértice de un penteracto en 3 dimensiones. Los 32 vértices de un 5-cubo se ubican en los 22 vértices exteriores del icosaedro rómbico, y los 10 vértices interiores restantes forman un antiprisma pentagonal.

De la misma manera, se puede obtener un dodecaedro de Bilinski de un teseracto, y un triacontaedro rómbico de un hexeracto.

Poliedros relacionados

El icosaedro rómbico se puede derivar del triacontaedro rómbico quitando uno de los cinturones de las 10 caras intermedias.


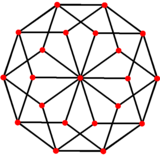
Un triacontaedro rómbico puede verse como un icosaedro rómbico elongado
El icosaedro rómbico y el triacontaedro rómbico tienen la misma proyección ortogonal con simetría de orden 10 (*)

(*) (Por ejemplo, en la figura de la izquierda):

La proyección ortogonal del cinturón (vertical) de las 10 caras medias del triacontaedro rómbico es simplemente el decágono regular exterior (horizontal) de la proyección ortogonal común.

Un icosaedro rómbico

Referencias

  1. ↑ Weisstein, Eric W. «Rhombic Icosahedron». mathworld.wolfram.com (en inglés). Consultado el 20 de diciembre de 2019. 

Enlaces externos