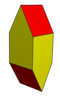
En geometría y cristalografía, un estereoedro es un politopo convexo que rellena el espacio isoédricamente,[1] lo que significa que la simetría del teselado permite trasladar cualquier tesela estereoédrica hasta hacerla coincidir con cualquier otra.
Los análogos bidimensionales de los estereoedros se denominan planígonos. Los politopos de dimensiones superiores también pueden ser estereoedros, aunque sería más exacto llamarlos estereotopos.
Plesioedros
Los plesioedros son un subconjunto de los estereoedros,[2] definidos como las celdas de Voronoi de un conjunto de Delaunay simétrico.
Los paraleloedros son plesioedros que rellenan el espacio empleando únicamente la traslación. Las aristas representadas con el mismo color son paralelas entre sí.
Otros estereoedros periódicos
La teselación catóptrica contiene células estereoédricas. Los ángulos diedros son divisores enteros de 180°, y están coloreados según su orden. Los primeros tres son los dominios fundamentales de simetría 
, 
y 
, representados por los diagramas de Coxeter-Dynkin siguientes: 
, 
y 
. es una media simetría de y es un cuarto de simetría.
Cualquier estereoedro que llene el espacio mediante operaciones de simetría se puede diseccionar en celdas idénticas más pequeñas que también son estereoedros. Los modificadores de nombre empleados a continuación (mitad, cuarto y octavo) representan dichas disecciones.
Celdas catóptricas
| Caras
|
4 |
5 |
6 |
8 |
12
|
| Tipo
|
Tetraedro
|
Pirámide cuadrada
|
Bipirámide triangular
|
Cubo
|
Octaedro
|
Rombododecaedro
|
| Imágenes
|
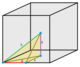
1/48 (1)
|
1/24 (2)
|
1/12 (4)
|
1/12 (4)
|
1/24 (2)
|
1/6 (8)
|
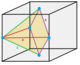
1/6 (8)
|
1/12 (4)
|
1/4 (12)
|
1 (48)
|
1/2 (24)
|
1/3 (16)
|
2 (96)
|
Simetría
(orden)
|
C1
1
|
C1v
2
|
D2d
4
|
C1v
2
|
C1v
2
|
C4v
8
|
C2v
4
|
C2v
4
|
C3v
6
|
Oh
48
|
D3d
12
|
D4h
16
|
Oh
48
|
| Panal
|
Octavo piramidal
|
Piramidal triangular
|
Tetraedral oblata
|
Medio piramidal
|
Cuarto piramidal cuadrado
|
Piramidal
|
Semioctaedral oblata
|
Cuarto octaedral oblata
|
Cuarto cúbica
|
Cúbica
|
Cúbica oblata
|
Octaedral oblata
|
Dodecaedral
|
Otros poliedros convexos que son estereoedros, pero no paraleloedros ni plesioedros, incluyen al girobifastigio.
Referencias
Bibliografía
- Ivanov, A. B. (2001), «Stereohedron&oldid=31579», en Hazewinkel, Michiel, ed., Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
- B. N. Delone, N. N. Sandakova, Teoría de los estereoedros Trudy Mat. Inst. Steklov., 64 (1961) págs. 28–51 (ruso)
- Goldberg, Michael Tres familias infinitas de rellenos espaciales tetraédricos Revista de teoría combinatoria A, 16, págs. 348–354, 1974.
- Goldberg, Michael The space-filling pentahedra, Journal of Combinatorial Theory, Serie A Volumen 13, Número 3, noviembre de 1972, páginas 437-443 /0097316572900775 PDF
- Goldberg, Michael El Pentaedro II que llena el espacio, Journal of Combinatorial Theory 17 (1974), 375–378. PDF
- Goldberg, Michael Sobre el hexaedro que llena el espacio Geom. Dedicata, junio de 1977, volumen 6, número 1, págs. 99–108 [1] -hexaedros.html PDF
- Goldberg, Michael Sobre los heptaedros que llenan el espacio Geometriae Dedicata, junio de 1978, volumen 7, número 2, págs. 175–184 [2] PDF
- Goldberg, Michael Rellenos espaciales poliédricos convexos de más de doce caras. Geom. Dedicata 8, 491-500, 1979.
- Goldberg, Michael Sobre los octaedros que llenan el espacio, Geometriae Dedicata, enero de 1981, volumen 10, número 1, págs. 323–335 [3] PDF Archivado el 22 de diciembre de 2017 en Wayback Machine.
- Goldberg, Michael Sobre el decaedro que llena el espacio. Topología Estructural, 1982, núm. Tipo 10-II PDF
- Goldberg, Michael Sobre los eneaedros que llenan el espacio Geometriae Dedicata, junio de 1982, volumen 12, número 3, págs. 297–306 [4] PDF
