|
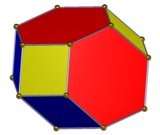
Dodecaedro elongado
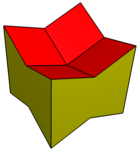
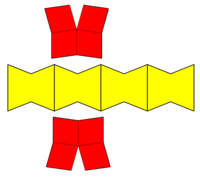
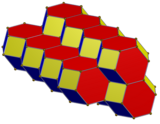
 En geometría, el dodecaedro elongado,[1] dodecaedro rómbico extendido, dodecaedro rombo-hexagonal[2] o dodecaedro hexarrómbico[3] es un dodecaedro convexo con 8 caras rómbicas y 4 caras hexagonales. Los hexágonos pueden hacerse equiláteros o regulares según la forma de los rombos. Puede verse como construido a partir de un rombododecaedro elongado mediante un prisma cuadrado. ParaleloedroJunto con el dodecaedro rómbico, es un poliedro que rellena el espacio, uno de los cinco tipos de paraleloedros identificados por Yevgraf Stepánovich Fiódorov que tesela el espacio cara a cara mediante traslaciones. Tiene 5 conjuntos de aristas paralelas, llamados zonas o cinturones. Teselación
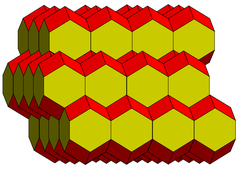
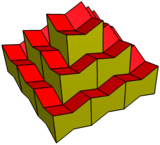
Está relacionado con el panal rómbico dodecaédrico con un alargamiento de cero. Proyectado en sentido normal a la dirección del alargamiento, el panal aparece como un teselado cuadrado, con un rombo proyectado en cada cuadrado. VariacionesEl dodecaedro expandido se puede distorsionar en volúmenes cúbicos, con el panal como un apilamiento de cubos semidesplazados. También se puede hacer cóncavo ajustando las 8 esquinas hacia abajo en la misma medida que los centros se mueven hacia arriba.
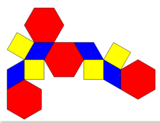
El dodecaedro elongado se puede construir como una contracción de un octaedro truncado uniforme, donde las caras cuadradas se reducen a aristas simples y las caras hexagonales regulares se reducen a caras rómbicas de 60 grados (o pares de triángulos equiláteros). Esta construcción alterna cuadrados y rombos en los vértices de 4 caras; y tiene la mitad de simetría, simetría D2h, orden 8.
Véase tambiénReferencias
Bibliografía
Enlaces externos
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia