|
Curva ROC
En la teoría de detección de señales, una curva ROC (acrónimo de Receiver Operating Characteristic, o Característica Operativa del Receptor) es una representación gráfica de la sensibilidad frente a la razón de falsas alarmas (1-especificidad) para un sistema clasificador binario según se varía el umbral de discriminación. Otra interpretación de este gráfico es la representación de la razón o proporción de verdaderos positivos (VPR = Razón de Verdaderos Positivos) frente a la razón o proporción de falsos positivos (FPR = Razón de Falsos Positivos) también según se varía el umbral de discriminación (valor a partir del cual decidimos que un caso es un positivo). ROC también puede significar Relative Operating Characteristic (Característica Operativa Relativa) porque es una comparación de dos características operativas (VPR y FPR) según cambiamos el umbral para la decisión. En español es preferible mantener el acrónimo inglés, aunque es posible encontrar el equivalente español COR. No se suele utilizar ROC aislado, debemos decir “curva ROC” o “análisis ROC”. Sobre la historia del acrónimo ROC consultar Swets (1996).[2] El análisis de la curva ROC, o simplemente análisis ROC, proporciona herramientas para seleccionar los modelos posiblemente óptimos y descartar modelos subóptimos independientemente de (y antes de especificar) el coste de la distribución de las dos clases sobre las que se decide. La curva ROC es también independiente de la distribución de las clases en la población (en diagnóstico, la prevalencia de una enfermedad en la población). El análisis ROC se relaciona de forma directa y natural con el análisis de coste/beneficio en toma de decisiones diagnósticas. La curva ROC se desarrolló por ingenieros eléctricos para medir la eficacia en la detección de objetos enemigos en campos de batalla mediante pantallas de radar, a partir de lo cual se desarrolla la Teoría de Detección de Señales (TDS). El análisis ROC se aplicó posteriormente en medicina, radiología, psicología y otras áreas durante varias décadas. Solo recientemente ha encontrado aplicación en áreas como aprendizaje automático (o machine learning en inglés), y minería de datos (data mining en inglés). Conceptos BásicosVer también: Error tipo I y tipo II Un modelo de clasificación (clasificador o diagnóstico) es una función que permite decidir qué elementos de un conjunto de instancias están relacionados o no por pertenecer a un mismo tipo o clase. El resultado del clasificador o del diagnóstico puede ser un número real (valor continuo), en cuyo caso el límite del clasificador entre cada clase debe determinarse por un valor umbral (por ejemplo para determinar si una persona tiene hipertensión basándonos en una medida de presión arterial), o puede ser un resultado discreto que indica directamente una de las clases. Consideremos un problema de predicción de clases binario, en la que los resultados se etiquetan positivos (p) o negativos (n). Hay cuatro posibles resultados a partir de un clasificador binario como el propuesto. Si el resultado de una exploración es p y el valor dado es también p, entonces se conoce como un Verdadero Positivo (VP); sin embargo si el valor real es n entonces se conoce como un Falso Positivo (FP). De igual modo, tenemos un Verdadero Negativo (VN) cuando tanto la exploración como el valor dado son n, y un Falso Negativo (FN) cuando el resultado de la predicción es n pero el valor real es p. Un ejemplo aproximado de un problema real es el siguiente: consideremos una prueba diagnóstica que persiga determinar si una persona tiene una cierta enfermedad. Un falso positivo en este caso ocurre cuando la prueba predice que el resultado es positivo, cuando la persona no tiene realmente la enfermedad. Un falso negativo, por el contrario, ocurre cuando el resultado de la prueba es negativo, sugiriendo que no tiene la enfermedad cuando realmente sí la tiene. Definamos un experimento a partir de P instancias positivas y N negativas. Los cuatro posibles resultados se pueden formular en una Tabla de contingencia (o Matriz de confusión) 2x2 como sigue:
El espacio ROC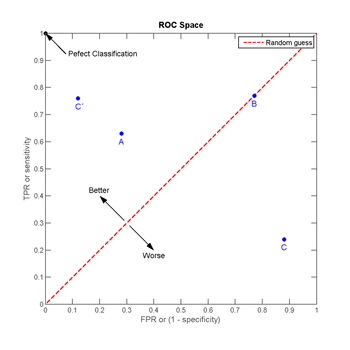 La tabla de contingencia puede proporcionar varias medidas de evaluación (ver caja de terminología). Para dibujar una curva ROC solo son necesarias las razones de Verdaderos Positivos (VPR) y de falsos positivos (FPR). La VPR mide hasta qué punto un clasificador o prueba diagnóstica es capaz de detectar o clasificar los casos positivos correctamente, de entre todos los casos positivos disponibles durante la prueba. La FPR define cuántos resultados positivos son incorrectos de entre todos los casos negativos disponibles durante la prueba. Un espacio ROC se define por FPR y VPR como ejes x e y respectivamente, y representa los intercambios entre verdaderos positivos (en principio, beneficios) y falsos positivos (en principio, costes). Dado que VPR es equivalente a sensibilidad y FPR es igual a 1-especificidad, el gráfico ROC también es conocido como la representación de sensibilidad frente a (1-especificidad). Cada resultado de predicción o instancia de la matriz de confusión representa un punto en el espacio ROC. El mejor método posible de predicción se situaría en un punto en la esquina superior izquierda, o coordenada (0,1) del espacio ROC, representando un 100% de sensibilidad (ningún falso negativo) y un 100% también de especificidad (ningún falso positivo). A este punto (0,1) también se le llama una clasificación perfecta. Por el contrario, una clasificación totalmente aleatoria (o adivinación aleatoria) daría un punto a lo largo de la línea diagonal, que se llama también línea de no-discriminación, desde el extremo inferior izquierdo hasta la esquina superior derecha (independientemente de los tipos de base positivas y negativas). Un ejemplo típico de adivinación aleatoria sería decidir a partir de los resultados de lanzar una moneda al aire, a medida que el tamaño de la muestra aumenta, el punto de un clasificador aleatorio de ROC se desplazará hacia la posición (0.5, 0.5). La diagonal divide el espacio ROC. Los puntos por encima de la diagonal representan los buenos resultados de clasificación (mejor que el azar), puntos por debajo de la línea de los resultados pobres (peor que al azar). Nótese que la salida de un predictor consistentemente pobre simplemente podría ser invertida para obtener un buen predictor. Considérense los siguientes cuatro resultados de 100 instancias positivas y otras 100 negativas:
En la figura de la derecha se muestran los puntos que los cuatro ejemplos anteriores en el espacio ROC. El resultado del método A muestra claramente ser el mejor de entre los métodos A, B Y C. El resultado de B se encuentra sobre la línea de estimación aleatoria (diagonal); en la tabla se puede ver que la precisión (ACC) de este método es del 50%. El método C aparece como el peor de los tres, con un resultado muy pobre. Sin embargo, consideremos ahora la construcción de un cuarto método de predicción C' que simplemente invierte los resultados predichos por el método C. Este nuevo método mostrará una tabla de contingencia opuesta a la de C y su punto en el espacio ROC estará ahora por encima de la diagonal, y más próximo al punto de clasificación perfecta que el método A. Mientras C presentaba un pobre poder de predicción, a partir de él se ha construido un predictor mejor que todos los demás. Cuando el método C predice 'n' o 'p', el método C' predice 'p' o 'n' respectivamente. Siempre que un método presente un punto en el espacio ROC por debajo de la diagonal habrá que invertir sus predicciones para aprovechar su capacidad de predicción. Cuanto más cerca esté un método de la esquina superior izquierda (clasificación perfecta) mejor será, pero lo que en realidad marca el poder predictivo de un método es la distancia de este a la línea de estimación aleatoria, da igual si por arriba o por abajo. Curvas en el espacio ROCLos clasificadores discretos, como los Árbol de decisión o los sistemas de reglas, dan como resultados a valores numéricos una etiqueta binaria. Cuando se usan estos clasificadores con un conjunto concreto de instancias para clasificar o predecir, el rendimiento del clasificador proporciona un único punto en el espacio ROC. Para otros clasificadores, como un Clasificador bayesiano o una Red neuronal artificial, la salida son valores de probabilidad que representan hasta qué punto una instancia pertenece a una de las dos clases. Para estos métodos se debe fijar un valor umbral que determinará un punto en el espacio ROC. Por ejemplo, si ante una determinada magnitud fijamos ese umbral en 0.8, la probabilidad de las instancias iguales o superiores serán predichas como positivas, y los valores por debajo serán predichos como negativos. Por tanto podremos calcular una tabla de contingencia (o matriz de confusión) para ese umbral de 0.8, y encontrar el punto correspondiente en el espacio ROC. Según vamos variando el umbral (por ejemplo, en pasos de 0.1) tendríamos una tabla de contingencia y un nuevo punto en el espacio ROC. Dibujar la curva ROC consiste en poner juntos todos los puntos correspondientes a todos los umbrales o puntos de corte, de tal modo que ese conjunto de puntos se parecerá más o menos a una curva en el espacio cuadrado entre (0,0) y (1,1). Dependiendo del tipo de modelo la curva se parecerá más a una escalera (métodos no paramétricos) o una verdadera curva (métodos paramétricos).[3] A medida que desplazamos ese valor umbral, en realidad estamos alterando las tasas de verdaderos positivos (VP) y falsos positivos (FP). Cómo se puede interpretar una curva ROCLa curva ROC se puede usar para generar estadísticos que resumen el rendimiento (o la efectividad, en su más amplio sentido) del clasificador. A continuación se proporcionan algunos:
El indicador más utilizado en muchos contextos es el área bajo la curva ROC o AUC. Este índice se puede interpretar como la probabilidad de que un clasificador ordenará o puntuará una instancia positiva elegida aleatoriamente más alta que una negativa. Se puede demostrar que el área bajo la curva ROC es equivalente a la Prueba de Mann-Whitney, una prueba no paramétrica aplicada a dos muestras independientes, cuyos datos han sido medidos al menos en una escala de nivel ordinal. Se trata de una prueba estadística virtualmente idéntica a la realización de una prueba paramétrica ordinaria T de dos muestras en los datos después de haber ordenado las muestras combinadas. Es también equivalente a la Prueba de los signos de Wilcoxon. También se ha demostrado la relación del área bajo la curva ROC con el Coeficiente de Gini, con la siguiente fórmula , donde: Otra forma básica de calcular AUC es usando un promedio de una serie de aproximaciones trapezoidales. Sin embargo, se ha comentado que este indicador, en general, reducir la curva ROC en varios metros, hace perder información sobre el patrón de intercambios del algoritmo discriminador en cuestión. La comunidad de aprendizaje automático utiliza el estadístico AUC para la comparación de modelos. En otras áreas de ingeniería se prefiere la medida del área entre la curva ROC y la línea de no-discriminación. Finalmente en Psicofísica (preferible consultar la versión inglesa en [1]) se utiliza preferentemente d'. La ilustración que abre este artículo muestra el uso de los gráficos ROC para la comparación de la capacidad predictiva de varios algoritmos predictivos basados en epítopes. Si quisieras descubrir como mínimo el 60% de los epítopes en una proteína de un virus, se puede observar en el gráfico cómo alrededor de un tercio de los resultados estarían marcados erróneamente como epítopes. La información que no es visible en este gráfico es qué umbrales va a utilizar la persona que usa los algoritmos. En resumen: se trata de una medida pura de la eficacia o capacidad predictiva del sistema, independientemente del punto de corte que se utilice, de las reglas de las personas que usen los sistemas predictivos y también, y muy importante, de las tasas de verdaderos positivos en la población (o Prevalencia en contextos de diagnóstico médico). En ocasiones puede ser más útil mirar a una región específica de la curva ROC más que a toda la curva. Es posible calcular áreas parciales bajo la curva, o AUC parciales. Por ejemplo, nos podríamos concentrar en la región de la curva con razones de falsos positivos más bajas, que es a menudo el interés principal de las pruebas de Detección precoz (o (medicine)|screening en la población. Curvas ROC para pruebas diagnósticas Para la elección entre dos pruebas diagnósticas distintas, se recurre a las curvas ROC, ya que es una medida global e independiente del punto de corte. Por esto, en el ámbito sanitario, las curvas ROC también se denominan curvas de rendimiento diagnóstico. La elección se realiza mediante la comparación del área bajo la curva (AUC) de ambas pruebas. Esta área posee un valor comprendido entre 0,5 y 1, donde 1 representa un valor diagnóstico perfecto y 0,5 es una prueba sin capacidad discriminatoria diagnóstica. Es decir, si AUC para una prueba diagnóstica es 0,8 significa que existe un 80% de probabilidad de que el diagnóstico realizado a un enfermo sea más correcto que el de una persona sana escogida al azar. Por esto, siempre se elige la prueba diagnóstica que presente un mayor área bajo la curva. A modo de guía para interpretar las curvas ROC se han establecido los siguientes intervalos para los valores de AUC: (Falta referencia) [0.5]: Es como lanzar una moneda. [0.5, 0.6): Test malo. [0.6, 0.75): Test regular. [0.75, 0.9): Test bueno. [0.9, 0.97): Test muy bueno. [0.97, 1): Test excelente. HistoriaLa curva ROC se comenzó a utilizar durante la Segunda Guerra Mundial para el análisis de señales de radar, a partir de lo cual se desarrolló la Teoría de Detección de Señales. Después del ataque a Pearl Harbor en 1941, el ejército de los Estados Unidos comenzó un programa de investigación para detectar correctamente los aparatos japoneses a partir de sus señales de radar. En los años 50, las curvas ROC se utilizaron en Psicofísica para evaluar la capacidad de detección de humanos (y también de no humanos) en señales débiles. En medicina el análisis ROC se ha utilizado de forma muy extensa en epidemiología e investigación médica, de tal modo que se encuentra muy relacionado con la medicina basada en la evidencia. En radiología, el análisis ROC es la técnica de preferencia para evaluar nuevas técnicas de diagnóstico por imagen. Más recientemente, las curvas ROC se han mostrado muy útiles para la evaluación de técnicas de aprendizaje automático. La primera aplicación de las ROC en esta área fue por Spackman, quien demostró el valor de las curvas ROC para la comparación de diferentes algoritmos de clasificación. Referencias
Otras referencias esenciales
Enlaces externos
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia











