|
Conformación de pulsoEn electrónica y telecomunicaciones la conformación de pulso es el proceso de cambiar la forma de onda de los pulsos transmitidos. Su propósito es el de minimizar el ancho de banda de la señal transmitida a la vez que se limita la interferencia entre símbolos .[1] Generalmente, la conformación de pulso ocurre después de la codificación en línea y la modulación. Necesidad de la conformación de pulsoLa transmisión de una señal a una tasa de modulación alta, a través de un canal limitado en banda puede crear interferencia entre símbolos. Mientras la tasa de modulación aumenta, también lo hace el ancho de banda de la señal. Cuando el ancho de banda de la señal se hace mayor al del canal, este comienza a introducir distorsión a la señal, la cual se manifiesta mediante la interferencia entre símbolos. El espectro de la señal transmitida está determinado por el filtro de conformación de pulsos que se halla en el transmisor. Generalmente, los símbolos transmitidos son representados como una secuencia de pulsos delta de Dirac. Esta "señal teórica" es luego filtrada por el filtro de conformación de pulsos, por lo que el espectro de esta señal es determinado por tal filtro. La transformada de Fourier de los pulsos transmitidos tiene la forma sen(x)/x, la cual tiene potencia de señal significativa a frecuencias superiores a la tasa de símbolos. Esto no representa un gran problema cuando se usan el cable de fibra óptica o el cable de par trenzado como canal de transmisión. Sin embargo, en comunicaciones por radiofrecuencia esto sería malgastar ancho de banda y las bandas de frecuencia muy específicas se utilizan para transmisiones individuales. En otras palabras, el canal para la señal es de banda limitada. Por esta razón se han desarrollado mejores filtros que tratan de minimizar el ancho de banda necesario para una determinada velocidad de símbolos. Un ejemplo en otras áreas de la electrónica es la generación de pulsos con tiempo de subida corto; una manera de hacerlo es comenzar con un pulso con un tiempo de subida mayor, y disminuir el tiempo de subida, por ejemplo, con un circuito basado en el diodo de almacenamiento de carga.... Filtros de conformación de pulsos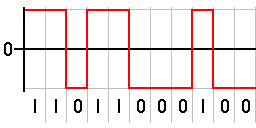 No todo filtro puede ser utilizado como un filtro de conformación de pulsos. El filtro en sí no debe introducir interferencia entre símbolos, lo que necesita para satisfacer ciertos criterios. El primer criterio de Nyquist es comúnmente utilizado para la evaluación, porque se relaciona el espectro de frecuencia de la señal del transmisor con la interferencia entre símbolos. Ejemplos de filtros de conformación de pulsos que se encuentran comúnmente en sistemas de comunicación son:
La conformación de pulsos en el lado trasmisor se combina a menudo con un filtro adaptado en el lado receptor para lograr la tolerancia óptima para el ruido en el sistema. En este caso, la conformación de pulso se distribuye por igual entre los filtros del emisor y del receptor. Las respuestas en amplitud de los filtros son así raíces cuadradas puntuales de los filtros del sistema. Se han inventado otros enfoques que eliminan los filtros de conformación de impulsos complejos. En OFDM, las portadoras se modulan tan lentamente que cada portadora es casi independiente de las limitaciones de ancho de banda del canal. Filtro SincEs también conocido como el filtro pasabajo ideal, el cual es irrealizable,[2] aunque en teoría es el mejor filtro de conformación de pulsos. Es un filtro no causal con extremos de decaimiento relativamente lentos. También es problemático desde el punto de vista de sincronización ya que cualquier error de fase resulta en una abruptamente creciente interferencia entre símbolos de sincronización. Filtro de coseno alzado Esta clase de filtro es de fácil implementación y de amplio uso. Es utilizado frecuentemente en sistemas de telecomunicaciones debido a que es capaz de reducir al mínimo la interferencia entre símbolos. Se llama así porque la parte no nula del espectro frecuencial es un coseno que, en su forma más simple (), se encuentra 'alzado' para situarse por encima del eje horizontal de frecuencias . Filtro gaussianoSe le denomina así ya que su respuesta a un pulso es similar a una función gaussiana. Véase tambiénReferencias
|
Portal di Ensiklopedia Dunia

