|
Cifrado César
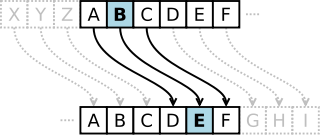
En criptografía, el cifrado César, también conocido como cifrado por desplazamiento, código de César o desplazamiento de César, es una de las técnicas de cifrado más simples y más usadas. Es un tipo de cifrado por sustitución en el que una letra en el texto original es reemplazada por otra letra que se encuentra un número fijo de posiciones más adelante en el alfabeto. Por ejemplo, con un desplazamiento de 3, la A sería sustituida por la D (situada 3 lugares a la derecha de la A), la B sería reemplazada por la E, etc. Este método debe su nombre a Julio César, que lo usaba para comunicarse con sus generales. El cifrado César muchas veces puede formar parte de sistemas más complejos de codificación, como el cifrado Vigenère, e incluso tiene aplicación en el sistema ROT13. Como todos los cifrados de sustitución alfabética simple, el cifrado César se descifra con facilidad y en la práctica no ofrece mucha seguridad en la comunicación. EjemploLa transformación se puede representar alineando dos alfabetos; el alfabeto cifrado es un alfabeto normal que está desplazado un número determinado de posiciones hacia la izquierda o la derecha. Por ejemplo, aquí el cifrado César está usando un desplazamiento de seis espacios hacia la derecha: Texto original: ABCDEFGHIJKLMNÑOPQRSTUVWXYZ Para codificar un mensaje, simplemente se debe buscar cada letra de la línea del texto original y escribir la letra correspondiente en la línea codificada. Para decodificarlo se debe hacer lo contrario. Texto original: WIKIPEDIA, LA ENCICLOPEDIA LIBRE La codificación también se puede representar usando aritmética modular, transformando las letras en números, de acuerdo al esquema A = 0, B = 1, ..., Z = 26.[1] En inglés el módulo es 26 por emplear 26 símbolos. En español, 27. Debe emplearse el número de símbolos del alfabeto. La codificación de la letra x con un desplazamiento n puede ser descrita matemáticamente como:[2] La decodificación se hace de manera similar: La operación de sustitución se conserva siempre a lo largo de todo el mensaje, por lo que el cifrado se clasifica como un cifrado de tipo sustitución monoalfabética, en oposición a la sustitución polialfabética. Historia y uso El cifrado César recibe su nombre en honor a Julio César, que, según Suetonio, lo usó con un desplazamiento de tres espacios para proteger sus mensajes importantes de contenido militar:
Aunque César es la primera persona de la que se sabe que haya usado este sistema, anteriormente ya se utilizaron otros cifrados por sustitución. El sobrino de Julio César, Augusto, también empleó el cifrado, pero con un desplazamiento de uno:
Hay indicios de que Julio César usaba también sistemas más complicados, y un escritor, Aulus Gellius, hace referencia a un tratado (ahora perdido) sobre el cifrado:[3]
No se sabe cuán efectivo resultaba realmente el cifrado César en esa época, pero debió de ser razonablemente seguro, ya que pocos enemigos de César habrían sabido leer, y mucho menos podrían haber llevado a cabo el criptoanálisis necesario. Asumiendo que el atacante pudiera leer el mensaje, no existen pruebas de la existencia de técnicas para solucionar este tipo de codificación.[4] En el siglo XIX, la sección de avisos personales de los periódicos servía a veces para intercambiar mensajes codificados usando técnicas de cifrado simples. David Kahn (1967) describe algunos ejemplos de comunicación secreta entre amantes que utilizaban este cifrado en el periódico The Times.[5] Incluso en 1915, el cifrado César aún era utilizado: la armada rusa lo empleaba sustituyendo a otros cifrados más complicados que habían resultado muy difíciles de utilizar por sus tropas; los criptoanalistas alemanes y austriacos no tuvieron mucha dificultad para decodificar los mensajes.[6] El cifrado César se puede encontrar en la actualidad en algunos juguetes modernos, como los anillos decodificadores. En el algoritmo ROT13 se usa el cifrado César con un desplazamiento de 13, un método simple para ofuscar el texto que se usa en algunos foros de internet para ocultar texto (como la línea final de un chiste o partes de una historia que no se quieren revelar), pero no se usa como método de codificación.[7] El cifrado Vigenère usa el cifrado César con un desplazamiento diferente en cada posición del texto; el valor del desplazamiento se define usando una palabra clave repetitiva. Si la palabra clave fuera escogida al azar y tan larga como el mensaje (para que no se repita), el sistema resultante sería, en teoría, indescifrable. Para claves más cortas que el mensaje (es decir, por el cifrado Vigenère), que es lo que se usaba históricamente, aparece en el texto un patrón cíclico que se puede detectar con el método Kasiski, y saber la longitud de la clave. Una vez conocida la longitud de la clave, por ejemplo k, entonces el criptograma se descompone en criptogramas k de César que se pueden descifrar con un análisis frecuencial.[8] A modo anecdótico, cabe señalar también que el capo mafioso Bernardo Provenzano, recientemente detenido, utilizaba para comunicarse, en pleno siglo XXI, notas escritas con una máquina de escribir, codificadas mediante este rudimentario algoritmo, renegando de cualquier tecnología nueva como el teléfono móvil o internet. A pesar de lo rudimentario del sistema, ha conseguido tener a la policía despistada durante años.[9] Descifrado
El descifrado del cifrado César puede hacerse fácilmente, incluso si solo se dispone de un texto cifrado corto. Se pueden considerar dos situaciones:
En la primera situación se pueden aplicar dos métodos. El primero se basa en un ataque de fuerza bruta:[10] como solo existe un determinado número de valores de desplazamiento, 27 en español, se pueden probar todos y cada uno hasta encontrar un mensaje coherente.[11] Una forma de hacer esto es usar una tabla y en cada renglón escribir el texto con un desplazamiento diferente.[12] El ejemplo de texto cifrado dado en la tabla de la derecha es "Ep exeuyi"; se puede reconocer el mensaje original a simple vista con un desplazamiento de cuatro. En la segunda situación, el proceso de descifrado es aún más directo. Como solo hay un número limitado de posibles desplazamientos, se pueden probar todos por orden, en un ataque por fuerza bruta.[13] Una forma de hacerlo es escribir una tabla en la que se descifra un pedazo del texto con todos los desplazamientos posibles[14] —esta técnica a veces se conoce como «completando el componente claro»—.[15] En el ejemplo de la tabla de la derecha se intenta decodificar el texto cifrado «Ep exeuyi»; en este caso, el texto coherente se reconoce instantáneamente a simple vista, encontrándose codificado por un desfase de cinco letras hacia la izquierda. Otra forma de obtener la solución mediante este método es escribiendo debajo de cada letra el alfabeto en orden inverso y empezando por esa letra. Este proceso se puede acelerar usando cintas verticales con el alfabeto escrito en orden inverso y alineado, de modo que formen el texto cifrado en una fila. Así, el texto coherente debe aparecer en alguna de las filas.  El segundo método de descifrado consiste en comparar las distribuciones de frecuencias de las letras (análisis de frecuencia). Representando las frecuencias de las letras en el texto cifrado y conociendo la distribución de letras en el idioma original del mensaje original, una persona puede determinar fácilmente el valor del desplazamiento. Por ejemplo, en español, las frecuencias de las letras E y A (las más frecuentes) y las de la K y la W (las menos frecuentes) son particularmente distinguibles.[16] Los ordenadores también pueden hacerlo a base de mediciones, haciendo que la distribución actual coincida con la distribución esperada (se puede utilizar por ejemplo un análisis de distribución chi cuadrado).[17] La mayoría de las veces solo se encontrará un mensaje descifrado. Sin embargo, cuando el mensaje es muy corto pueden aparecer varias palabras descifradas. Por ejemplo, "ezaz" puede ser descifrado como "topo" o "jefe"; de manera similar "xzyz" puede ser descifrado como "cede" o "mono". Repetir el proceso de cifrado varias veces no mejora la seguridad. Esto se debe a que usar dos desplazamientos, por ejemplo el desplazamiento A y el desplazamiento B, sería equivalente a usar un desplazamiento de A + B. En terminología matemática, el cifrado repetido con diferentes claves forma un grupo.[18] Véase tambiénReferencias
Bibliografía
Enlaces externos |
||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia