|
Centralidad A) intermediación B) cercanía C) vector propio D) grado E) centralidad armónica F) centralidad de Katz Las tonalidades van del rojo (más centrales) al azul (más periféricos). En teoría de grafos y análisis de redes sociales, el concepto de centralidad refiere a la importancia o prominencia de los vértices (o nodos o actores) dentro de un grafo o red social.[1] Existen cientos de medidas o índices de centralidad, para determinar y comparar cuantitativamente la importancia relativa de un actor dentro de la estructura definida por la red.[2] Usualmente estas medidas se normalizan para retornar valores entre 0 y 1, de modo de poder hacer comparaciones entre distintas redes y casos de estudio.[1] La centralidad no es un atributo intrínseco de los nodos o actores de una red, como podrían serlo la autoestima, la temperatura, el ingreso monetario, etc. sino un atributo estructural, es decir, un valor asignado que depende de las relaciones del actor con los demás actores de la red. Intuitivamente (aunque dependerá de la medida de centralidad utilizada), en un grafo estrella o red egocéntrica el nodo central debería tener la mayor centralidad, mientras que los nodos periféricos compartirían todos un mismo valor de centralidad, inferior al del centro.[1] El concepto fue introducido inicialmente por Alex Bavelas en 1948.[3] Es uno de los conceptos más estudiados en el análisis de redes sociales,[4][5] y muchos de los conceptos relacionados con las medidas de centralidad reflejan su origen sociológico.[6] En ocasiones, en el caso de relaciones dirigidas o asimétricas, esto es, redes representadas como grafos dirigidos, en lugar de hablar de «centralidad» se suele también hablar de medidas de prestigio o estatus,[7] aunque dependiendo del tipo de relaciones consideradas, también se podría hablar de «rango», «deferencia», «popularidad», etc.[1] En el análisis de redes sociales se suele distinguir también entre centralidad de actor y centralidad de grupo, siendo lo primero equivalente a la noción de centralidad utilizada en este artículo, mientras que la centralidad de grupo, al concepto asociado a la centralización.[1] HistoriaEl estudio de la centralidad en los sociogramas y las redes sociales se inició a fines de los años 1940 e inicios de los años 1950,[8][9] de forma paralela a los primeros estudios formales de cliques o camarillas en sociomatrices.[10][11] Más concretamente, el concepto de centralidad se le adjudica al psicosociólogo Alex Bavelas, por un trabajo de 1948 en que presentó un modelo matemático para grupos en estructuras sociales.[3] A partir de este tipo de estudios es que se introdujo la teoría de grafos como herramienta clave para el análisis de redes sociales.[12] Definiciones y caracterizaciones de centralidadUna medida (o índice) de centralidad es una fórmula o algoritmo que permite medir la importancia o prominencia de los vértices o actores en un grafo o red social. Sin embargo, para decidir acerca de la validez de un índice de centralidad, es necesario definir primero el significado de esa «importancia» o «prominencia» que se busca medir. En este sentido, y de manera muy general, los actores más centrales o prominentes se pueden definir como aquellos que están ampliamente implicados en relaciones con otros actores. Por lo tanto, un actor central es uno que está implicado (no necesariamente de forma directa) en muchos lazos. Para el caso de grafos dirigidos (o redes asimétricas), un actor prestigioso (o con estatus, rango, deferencia o popularidad, dependiendo de lo que representen las relaciones) es un actor que es objeto o receptor de muchos lazos.[1] Medidas de centralidadLas medidas de centralidad se pueden agrupar en dos categorías: medidas radiales (radial measures) y mediales (medial measures).[13] Las primeras toman como punto de referencia un nodo dado que inicia o termina recorridos por la red, mientras que las segundas toman como referencia los recorridos que pasan a través de un nodo dado.[14] Las medidas radiales a su vez se pueden clasificar en medidas de volumen y de longitud, según el tipo de recorridos que consideran. Las primeras miden el volumen (o el número) de recorridos limitados a dicha longitud prefijada, en tanto que las segundas miden la longitud de los recorridos necesarios para alcanzar un volumen prefijado.[14] Desde la formulación realizada por Bavelas (1948), se han propuesto diversas medidas de centralidad de un nodo. Existen cuatro medidas clásicas que son ampliamente usadas en el análisis de redes sociales:
Para algunas de estas medidas existen a su vez versiones más generales o bien generalizaciones para las redes con pesos.[15] Adicionalmente, se puede distinguir entre las medidas «absolutas» de centralidad, que indican un valor no comparable y aquellas que están normalizadas, denominadas medidas «relativas» de centralidad. En lo que sigue de esta sección, se define formalmente un grafo como un par ordenado , donde es su conjunto de nodos o vértices y su conjunto de aristas. El número de vértices se denota como . Un grafo también se puede representar como una matriz de adyacencia, donde cada posición asume el valor 1 cuando existe la arista , y el valor 0 cuando no existe. Centralidad de gradoLa centralidad de grado (en inglés, degree centrality) es la primera y más simple de las medidas de centralidad.[14] Corresponde sencillamente al grado de un nodo o actor, esto es, al número de aristas o lazos que posee un nodo con los demás.[16] Formalmente, para un grafo no dirigido (o red social de relaciones simétricas), si para cada nodo , denota el grado de dicho nodo, entonces su centralidad de grado se define como:[14] Si se tiene la matriz de adyacencia del grafo, entonces la centralidad de grado de un nodo se puede definir como:[1] Para normalizar esta medida, lo usual es dividir el grado de cada nodo por el número total de nodos de la red. En caso de que la red considerada sea un grafo simple (sin bucles), entonces basta con dividir por el número total de nodos menos 1. En caso de que el grado máximo para un grafo sea demasiado bajo, también se podría dividir por dicho grado máximo. Así, las siguientes son medidas de grado con normalizaciones aceptables:
Para grafos dirigidos (o redes sociales con relaciones asimétricas), se pueden definir dos medidas de centralidad de grado diferentes, correspondientes al grado de entrada y al grado de salida, es decir, respectivamente:
y como matrices de adyacencia:
Ambas se consideran medidas de prestigio. Dependiendo del contexto, en análisis de redes sociales el grado de entrada podría interpretarse como una medida de popularidad, mientras que el grado de salida como una de actividad o sociabilidad.[1] En complejidad computacional, el cálculo de esta medida toma para un grafo denso, y para un grafo disperso. Variantes del gradoEl grado de un nodo puede verse como el número de caminos de longitud 1 que lo conectan con otros nodos. Una generalización natural a la centralidad de grado, es la centralidad de camino-k (en inglés, k-path centrality) que para cada nodo mide el número de caminos de largo «a lo más » que lo conectan a otros nodos.[14] En un grafo no dirigido, esta medida equivale a la cardinalidad de la vecindad del nodo, considerando una profundidad . Otra variante es la densidad de ego,[17][18] donde en lugar de normalizar por el número de nodos o el máximo grado, se escoge el máximo número de aristas posible de la red.[1] Así, para un grafo no dirigido, dependiendo de si el grafo no admite bucles o sí los permite, se tiene, respectivamente:
Si el grafo es dirigido, entonces se tiene, sin bucles y con bucles, respectivamente:
En caso de que solo se divida por el número de aristas del grafo en cuestión,[1] entonces se obtiene el alcance (en inglés, span) del nodo:[19][20] También para grafos dirigidos, se define un índice de sociación como la diferencia entre la densidad o media de la «intensidad» total de la red, y el grado de salida o «elecciones» realizadas por el actor:[21][1] Centralidad de cercaníaLa centralidad de cercanía, o simplemente cercanía (en inglés, closeness), es la más conocida y utilizada de las medidas radiales de longitud. Se basa en calcular la suma o bien el promedio de las distancias geodésicas (o longitudes de los caminos más cortos) desde un nodo hacia todos los demás.[14] Note que mientras mayor sea la «distancia» entre dos vértices, menor será la «cercanía» entre estos. Por lo tanto, la cercanía se define como el inverso multiplicativo de la «lejanía» entre dos vértices.[22] Formalmente, para un grafo (dirigido o no dirigido), sea la distancia geodésica entre los nodos y , la cercanía de un nodo se define como:[1] Note que en algunas referencias puede cambiar por .[23] Sea la matriz de distancias de la red, es decir, aquella matriz cuyos elementos corresponden a la distancia geodésica desde el nodo hasta el nodo , entonces una definición alternativa es la siguiente: Para normalizar esta medida, se considera el mayor valor posible que podría asumir la medida para un nodo. Si el grafo no admite bucles, entonces un nodo a lo más puede conectarse directamente a los nodos restantes; si admite bucles (y asumimos que no es un multigrafo), entonces podrá conectarse directamente con los nodos de la red. Por lo tanto, la medida normalizada queda definida formalmente, para ambos casos, respectivamente:
En una red de flujo esta medida se puede interpretar como el tiempo de llegada a destino de algo que fluye a través de la red.[24] También puede interpretarse como la rapidez que tomará la propagación de la información desde un nodo a todos los demás.[25] La cercanía mide de alguna forma la accesibilidad de un nodo en la red. Este concepto es utilizado también de manera similar en topología, donde se define como un espacio métrico. Note que en un grafo disconexo, la cercanía de todos los vértices será siempre igual a 0, dado que siempre existirá algún otro nodo para el cual la distancia geodésica con él resulta infinita. Por lo tanto, la centralidad de cercanía tiene la desventaja de que solo se puede aplicar, en el caso de redes no dirigidas, sobre grafos conexos o componentes conexos, y para redes dirigidas, sobre componentes fuertemente conexos.[1] Variantes de la cercaníaEn lugar de considerar la suma de las distancias geodésicas de un nodo hacia todos los demás, existe una variante que se enfoca únicamente en hallar la menor de estas distancias geodésicas. La excentricidad de un nodo es la mayor distancia entre ese nodo y cualquier otro del grafo. El centro de Jordan refiere al subconjunto de nodos con menor excentricidad dentro del grafo. Este centro puede encontrarse fácilmente a partir de la matriz de distancias del grafo, seleccionando aquellos nodos que comparten el menor valor máximo de sus respectivas filas en la matriz.[1] Un concepto relacionado muy antiguo es el de centroide, más apropiado específicamente para árboles.[26] La idea es que para cada nodo del árbol, se considera el peso de cada una de sus ramas o caminos que parten desde dicho nodo, donde el peso de una rama es su número de aristas. El nodo se queda con el mayor de los pesos resultantes de entre todas sus ramas. El centroide corresponde así al subconjunto de nodos que comparten el peso final más pequeño.[1] La medida tradicional de cercanía asume que la propagación de información siempre se da en la red a través del camino más corto. Este modelo puede no ser el más realista para algunos tipos de escenarios de comunicación. Por ello han surgido algunas variantes de esta medida como la denominada cercanía por camino aleatorio (en inglés, random-walk closeness centrality), introducida por Noh y Rieger (2004) y que considera caminos aleatorios para acceder de un nodo a los demás, en lugar de escoger siempre el camino más corto.[27] Cercanía en grafos disconexosExisten algunas variantes de la cercanía que permiten trabajar con grafos disconexos. Si la red no es un componente fuertemente conexo, la centralidad armónica (harmonic centrality, en inglés) considera la suma del recíproco de las distancias en lugar del recíproco de la suma de las distancias, con la convención de que , esto es, que las distancias entre actores inaccesibles sea cero, en lugar de infinito:[28][29] En efecto, para grafos con distancias infinitas, la media armónica se comporta mejor que la media aritmética, que es la utilizada por la medida de cercanía tradicional.[30] Esta idea ha reaparecido varias veces en la literatura, usualmente sin el factor de normalización , por ejemplo para grafos no dirigidos, bajo el nombre de centralidad valorada (valued centrality, en inglés).[31] Otra alternativa natural es considerar únicamente los nodos accesibles desde o hacia el nodo cuya centralidad se está midiendo.[32] Sea el número de actores dentro del rango de influencia de (o accesibles desde o hacia , dependiendo de si se desea trabajar con aristas de salida o de llegada en un grafo dirigido, respectivamente), se puede definir la siguiente variante de la centralidad de cercanía: donde es la proporción de nodos accesibles en el componente conexo, y es la distancia media de los nodos a .[1] Una alternativa más distinta propone la siguiente medida de vulnerabilidad en las redes:[33] donde es nuevamente la matriz de distancias. Índices de prestigioPara redes dirigidas, la cercanía y sus variantes se suelen centrar en caminos desde un nodo dado. Sin embargo, también puede ser útil considerar los caminos hacia dicho nodo. A las medidas de centralidad que consideran este último tipo de caminos se les suele también llamar medidas o índices de prestigio.[1] El prestigio de proximidad de un nodo se define como: donde es el dominio de influencia del nodo , es decir, el conjunto de actores que pueden acceder a dicho actor, es la cardinalidad del dominio de influencia de , es la proporción de nodos de la red que están en el dominio de influencia de , y es la distancia media a la que los nodos del dominio de influencia están de . Note que el prestigio de proximidad se puede aplicar sobre redes disconexas.[1] Por otra parte, el estatus neto de un actor , que denotaremos , se define como:[34] donde la primera sumatoria es el estatus de , y la segunda sumatoria el contraestatus de .[1] Otro índice de prestigio conocido es el prestigio de rango, prestigio de estatus o centralidad de vector propio, que para cada actor considera no solo su propio prestigio, sino también el de los actores que apuntan a este. Bajo este criterio, un actor es más prestigioso en la medida que los actores relacionados con él son también más prestigiosos.[1] Centralidad de intermediación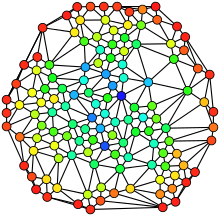 La centralidad de intermediación, o simplemente intermediación (en inglés, betweenness) es una medida que cuantifica la frecuencia o el número de veces que un nodo se encuentra entre las geodésicas o caminos más cortos de otros actores. Un actor tendrá una alta intermediación si es un vértice de corte para muchas geodésicas entre actores.[1][14] Formalmente, la intermediación de un nodo en una red o grafo se define como:[14] donde es el número de caminos más cortos desde el nodo hasta el nodo , y el número de caminos más cortos desde hasta que pasan a través del nodo . Para normalizar esta medida, y asumiendo que el grafo no tiene bucles o que estos no se consideran, se puede dividir por el mayor número posible de pares de actores, excluyendo el nodo que se está midiendo. Así, por lo tanto, para grafos no dirigidos y dirigidos se obtiene, respectivamente:[1]
En su versión normalizada, los valores de la medida siempre varían entre 0 y 1. Por ejemplo, para un grafo estrella, el nodo central tiene intermediación 1 y los nodos periféricos, intermediación 0. Note también que, a diferencia de la medida de cercanía clásica, la intermediación sí se puede calcular sobre grafos disconexos.[1] Los nodos con una alta intermediación suelen jugar un rol crítico en la estructura de la red, especialmente cuando hay grandes flujos de información que son transportados por nodos pertenecientes a grupos compactos. En una red social, este tipo de actores están relacionados con los agujeros estructurales (en inglés, structural holes), es decir, con aquellos nodos de los que depende la integración de algunas componentes de la red.[14] Los nodos que poseen una posición de intermediarios de alguna manera son también controladores o reguladores del flujo de información. Así, en un proceso de difusión, los nodos con una alta intermediación pueden actuar como brókers o «porteros» (en inglés, gatekeepers).[35] Adicionalmente, los actores con una alta intermediación también se pueden considerar como con una alta «influencia interpersonal».[1][4][36] En complejidad computacional, determinar el camino más corto para cada par de nodos de un grafo puede calcularse en tiempo (por ejemplo, usando el algoritmo de Floyd-Warshall) y utilizando un espacio .[14] En un grafo disperso, el algoritmo de Johnson puede lograr lo mismo en tiempo , y si el grafo es sin pesos, se puede lograr en tiempo y espacio utilizando el algoritmo de Brandes.[37] Variantes de la intermediaciónLa centralidad de intermediación tiene algunas restricciones. Si bien supone que todas las geodésicas tienen la misma probabilidad de ser elegidas, los actores con un alto grado podrían tener mayor probabilidades de ser elegidos para conectar otros actores, al pertenecer a más geodésicas entre actores. Bajo este razonamiento, solo en las redes regulares todos los actores tendrían la misma probabilidad de ser elegidos. Por otra parte, esta medida solo se centra en las geodésicas, pero en varios contextos (por ejemplo, en redes de telecomunicaciones) es razonable pensar en elegir caminos más largos que las geodésicas.[1] Existe una versión alternativa de la medida de intermediación basada en considerar caminos aleatorios del grafo, y no exclusivamente los más cortos. La idea es tomar en cuenta todos los caminos posibles, y calcular la medida de acuerdo a los elegidos aleatoriamente. Formalmente se define como:[14] donde es la matriz cuyos elementos contienen la probabilidad de ocurrencia de un camino al azar desde hasta y que contiene al nodo como nodo intermediario. Centralidad de informaciónLa centralidad de información nace de la idea de aplicar la teoría de la información en la definición de medidas de centralidad. Es una variante de la centralidad de intermediación que no se restringe solo a las geodésicas sino a todos los caminos posibles de la red. Esta medida está además motivada por la teoría de estimación estadística. Los pesos de los caminos se definen como las inversas de sus varianzas y representan la cantidad de información que circula a través de los respectivos actores. Dado que el flujo de información se asume independiente entre las aristas, entonces estas varianzas equivalen a las longitudes de los caminos. Las geodésicas normalmente asumen valores 1, mientras que los caminos más largos, valores inferiores, lo que representa una disminución de información. Esta medida determina la longitud media armónica de los caminos que acaban en un nodo , la que será pequeña si se conecta con muchos otros nodos a través de caminos cortos.[38][1] Centralidad de vector propioLa centralidad de vector propio mide la influencia de un nodo en una red. Fue propuesta por Phillip Bonacich en 1972,[39] y corresponde al principal vector propio de la matriz de adyacencia del grafo analizado.[14] Intuitivamente, los nodos que poseen un valor alto de esta medida de centralidad están conectados a muchos nodos que a su vez están bien conectados, también en este sentido; por lo tanto, son buenos candidatos para difundir información, divulgar rumores o enfermedades, etc. Los nodos más centrales en este sentido corresponden a centros de grandes grupos cohesivos. Mientras que en el caso de la centralidad de grado, cada nodo pesa lo mismo dentro de la red, en este caso la conexión de los nodos pesa de forma diferente. En general habrá varios valores propios para los cuales existe una solución de vector propio. Sin embargo, el requerimiento adicional de que las entradas de los vectores propios sean positivos implica (por el Teorema de Perron-Frobenius) que sólo los mayores valores propios conduzcan a la medida de centralidad deseada.[40] El método de las potencias es uno de los muchos algoritmos existentes para calcular el valor propio que puede ser utilizado para encontrar el vector propio dominante.[41] Además, este puede generalizarse tal que las entradas en la matriz de adyacencia puedan ser números reales representrando fuerzas de conexión, como en una matriz estocástica. Formalmente, sea la matriz de adyacencia de la red y su matriz transpuesta, la centralidad de vector propio de un nodo se define como:[1] Considerando el vector con las centralidades de todos los nodos de la red, se obtiene el siguiente sistema de ecuaciones lineales de ecuaciones y incógnitas:
donde es la matriz identidad de dimensión . Esta última es una ecuación característica donde es un autovector de que corresponde a un autovalor de . Este sistema de ecuaciones no tiene una solución finita,[42] por lo que de ella derivan distintas variaciones de esta medida de centralidad, dependiendo de cómo restringen o los índices de .[1] Variantes de vector propioLa mayoría de variaciones de la centralidad de vector propio buscan establecer ajustes de parámetros que permitan encontrar soluciones finitas al sistema de ecuaciones lineales de la definición original de la medida.[1] Aquí se cuentan la centralidad de Katz,[42] la centralidad de Hubbell,[43] la centralidad de Bonacich[44] o la centralidad alfa.[45] Hay algunas variaciones adicionales que se inspiran en la medida original para aplicaciones en dominios específicos, como es el caso de PageRank, creado originalmente para mejorar el motor de búsqueda del buscador de Google.[41] Centralidad de contribución (o basada en disimilaridades)Esta es una metodología relacionada con el uso de medidas de disimilaridad (propias de la teoría de clasificación y de la minería de datos) a fin de retroalimentar medidas de centralidad ya existentes en redes complejas. Mediante autocentralidad (o centralidad de vector propio), la metodología consiste en calcular la centralidad de cada nodo a través de la solución del problema de autovectores:[46] donde (producto coordenada a coordenada) y es una matriz de disimilaridades arbitraria, definida a través de una medida de disimilaridad, por ejemplo, el índice de Jaccard: donde esta medida nos permite cuantificar la contribución topológica de cada nodo (que es la razón por la que estas medidas son llamadas centralidades de contribución) en una red dada, teniendo más peso/relevancia aquellos nodos con mayor disimilaridad, puesto que estos permiten a un nodo dado acceder a aquellos nodos a los que no pueden acceder directamente. Cabe destacar que es no-negativa puesto que y son no-negativas, de manera que podemos aplicar el teorema de Perron Frobenius para asegurar que el problema de autovectores anterior tiene una única solución no-negativa para , permitiéndonos inferir la centralidad de cada nodo en la red. Por lo tanto, la centralidad del i-ésimo nodo estará dada por
donde es el número de nodos en la red. Varias redes y medidas de disimilaridad han sido probadas,[47] obteniéndose en todos los casos excelentes resultados. Véase tambiénReferencias
Bibliografía
|
||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia


























































































