Calendario perpetuo

Ilustración de la patente estadounidense 248872 de 1881, para un pisapapeles con calendario perpetuo. La sección superior se gira para revelar una de las siete listas de años (dividiendo los años bisiestos) para las que se aplican los siete calendarios siguientes

.

Un «calendario de bolsillo» de 50 años que se ajusta girando la esfera para colocar el nombre del mes debajo del año en curso. Así se puede deducir el día de la semana o la fecha

.

El calendario perpetuo es un sistema calendario que permite determinar de una manera sencilla el día de la semana para cualquier fecha, dentro de un amplio periodo que usualmente abarca muchos siglos.

Para los calendarios gregoriano y juliano, un calendario perpetuo consiste típicamente en una de tres variaciones generales:

1. Catorce calendarios de un año, más una tabla para mostrar qué calendario de un año se debe utilizar para cualquier año dado. Estos calendarios de un año se dividen uniformemente en dos conjuntos de siete calendarios: siete para cada año común (el año que no tiene un 29 de febrero) con cada uno de los siete comenzando en un día diferente de la semana, y siete para cada año bisiesto, de nuevo con cada uno comenzando en un día diferente de la semana, totalizando catorce. (Ver Carta dominical para un esquema de denominación común para los 14 calendarios).
2. Siete (31 días) calendarios de un mes (o siete cada uno de 28-31 días de duración del mes, para un total de 28) y una o más tablas para mostrar qué calendario se utiliza para un mes determinado. Las tablas de algunos calendarios perpetuos se deslizan unas contra otras, de modo que al alinear dos escalas entre sí se revela el calendario del mes específico a través de un puntero o mecanismo de ventana.[1]​ Los siete calendarios pueden combinarse en uno solo, ya sea con 13 columnas de las que sólo se revelan siete,[2]​[3]​ o con nombres de días de la semana móviles (como se muestra en la imagen del calendario perpetuo de bolsillo).
3. Una mezcla de las dos variantes anteriores: un calendario de un año en el que los nombres de los meses son fijos y los días de la semana y las fechas se muestran en piezas móviles que se pueden intercambiar según sea necesario.[4]​

Un calendario perpetuo de este tipo no indica las fechas de fiestas móviles como la Pascua, que se calculan basándose en una combinación de acontecimientos del año tropical y los ciclos lunares. Estas cuestiones se tratan con gran detalle en computus.

Un ejemplo temprano de calendario perpetuo para uso práctico se encuentra en el Nürnberger Handschrift GNM 3227a. El calendario abarca el periodo de 1390-1495 (por lo que el manuscrito se fecha en torno a 1389). Para cada año de este periodo, enumera el número de semanas entre Navidad y Quinquagesima. Este es el primer caso conocido de una forma tabular de calendario perpetuo que permite el cálculo de las fiestas móviles que se hicieron populares durante el siglo XV.[5]​

La capilla Cappella dei Mercanti, Turín contiene una máquina de calendario perpetuo realizada por Giovanni Plana mediante tambores giratorios.

Otros usos del término «calendario perpetuo»

Breguet classique Gran complicación calendario perpetuo

Las oficinas y los establecimientos comerciales suelen exhibir dispositivos que contienen un conjunto de elementos para formar todos los números posibles del 1 al 31, así como los nombres/abreviaturas de los meses y los días de la semana, para mostrar la fecha actual para comodidad de las personas que puedan estar firmando y fechando documentos como cheques. Los establecimientos que sirven bebidas alcohólicas pueden utilizar una variante que muestra el mes y el día actuales pero restando la edad legal de consumo de alcohol en años, lo que indica la última fecha legal de nacimiento para la compra de alcohol. Un dispositivo común consiste en dos cubos en un soporte. Un cubo lleva los dígitos del cero al cinco. El otro lleva los dígitos 0, 1, 2, 6 (o 9 si está invertido), 7 y 8. Esto es suficiente porque sólo el uno y el dos pueden aparecer dos veces en una fecha y están en ambos cubos, mientras que el 0 está en ambos cubos para que todas las fechas de un solo dígito puedan mostrarse en formato de dos dígitos. Además de los dos cubos, tres bloques, cada uno tan ancho como los dos cubos juntos, y un tercero tan alto y tan profundo, tienen los nombres de los meses impresos en sus caras largas. El mes en curso está girado hacia delante en el bloque frontal, con los otros dos bloques de meses detrás.

Ciertas reformas del calendarios han sido calificadas de calendarios perpetuos porque sus fechas se fijan todos los años en los mismos días de la semana. Algunos ejemplos son el Calendario Mundial, el Calendario fijo internacional y el Calendario Pax. Técnicamente, no se trata de calendarios perpetuos sino de calendarios perennes. Su propósito, en parte, es eliminar la necesidad de tablas de calendarios perpetuos, algoritmos y dispositivos de cálculo.

Reloj de pulsera con calendario perpetuo de Patek Philippe

En relojería, «calendario perpetuo» describe un mecanismo de calendario que muestra correctamente la fecha en el reloj «perpetuamente», teniendo en cuenta las diferentes duraciones de los meses así como los años bisiestos. El mecanismo interno desplazará la esfera al día siguiente.[6]​

Tipos de calendarios perpetuos

Los calendarios perpetuos consistían originalmente en una serie de tablas que permitían calcular el día de la semana de una fecha. Más recientemente se han hecho calendarios perpetuos implementados como dispositivos mecánicos, electrónicos, digitales, o programas de computadora.

Calendarios perpetuos basados en tablas

En los calendarios perpetuos en tablas, se usan varias tablas maestras para ayudar a conocer el día de la semana de una fecha. El uso de estas tablas evita hacer los cálculos complejos, ya que éstos están implícitos en la propia estructura de las tablas.

La forma exacta para usarlos varía de un calendario perpetuo a otro, pero, en líneas generales, de acuerdo a la fecha que se tenga hay que hacer una serie de búsquedas y cálculos aritméticos sencillos, dando como resultado un número que nos llevará a otra tabla en donde habrá que buscar otro número y calcular nuevamente, hasta que al final se llega a una última tabla en donde está el día de la semana de la fecha (domingo, lunes, martes, miércoles, jueves, viernes o sábado).

En el municipio de Noguera de Albarracín en Teruel (España), hay unas tablas conocidas como calendario perpetuo o almanaque de San Román situadas en la fachada de la iglesia.[7]​

Calendarios perpetuos con programas de computadoras

A día de hoy se implementan como programas de computadora que pueden mostrar el calendario de un mes o un año dentro de un período de siglos.

Algoritmos

Los calendarios perpetuos utilizan algoritmos para calcular el día de la semana para cualquier año, mes y día. Aunque las operaciones individuales en las fórmulas se pueden implementar de manera muy eficiente en el software, son complicadas de realizar mentalmente. Los diseñadores de calendarios perpetuos ocultan la complejidad en las tablas para simplificar su uso.

Un calendario perpetuo emplea una tabla para encontrar cuál de los catorce calendarios anuales usar. Una tabla para el calendario gregoriano expresa su gran ciclo de 400 años: 303 años comunes y 97 años bisiestos en total a 146 097 días, o exactamente 20 871 semanas. Este ciclo se divide en un período de 100 años con 25 años bisiestos, lo que hace 36 525 días, o un día menos de 5218 semanas completas; y tres períodos de 100 años con 24 años bisiestos cada uno, lo que hace 36 524 días, o dos días menos de 5218 semanas completas.

Dentro de cada bloque de 100 años, la naturaleza cíclica del calendario gregoriano procede de la misma manera que su predecesor juliano: un año común comienza y termina el mismo día de la semana, por lo que el año siguiente comenzará el siguiente día sucesivo de la semana. Un año bisiesto tiene un día más, por lo que el año siguiente a un año bisiesto comienza el segundo día de la semana posterior al comienzo del año bisiesto. Cada cuatro años, el día de la semana de inicio avanza cinco días, por lo que durante un período de 28 años, avanza 35, volviendo al mismo lugar tanto en la progresión del año bisiesto como en el día de la semana de inicio. Este ciclo se completa tres veces en 84 años, dejando 16 años en el cuarto ciclo incompleto del siglo.

Un factor de complicación importante en la construcción de un algoritmo de calendario perpetuo es la longitud peculiar y variable de febrero, que fue en un momento el último mes del año, dejando los primeros 11 meses de marzo a enero con un patrón repetido de cinco meses: 31, 30 , 31, 30, 31, ..., de modo que se pueda determinar fácilmente el desfase desde marzo del día de inicio de la semana para cualquier mes. La congruencia de Zeller, un algoritmo bien conocido para encontrar el día de la semana para cualquier fecha, define explícitamente enero y febrero como los meses 13 y 14 del año anterior para aprovechar esta regularidad, pero el mes-dependiente el cálculo sigue siendo muy complicado para la aritmética mental:

${\displaystyle \left\lfloor {\frac {(m+1)26}{10}}\right\rfloor \mod 7,}$

En cambio, un calendario perpetuo basado en una tabla es un mecanismo simple de consulta para determinar el desplazamiento del día de la semana para el primer día de cada mes. Para simplificar la tabla, en un año bisiesto enero y febrero deben ser tratados como un año separado o tener una entrada adicional en el mes de la tabla:

Mes	Enero	Febrero	Marzo	Abril	Mayo	Junio	Julio	Agosto	Septiembre	Octubre	Nov	Dic
Sumar	0	3	3	6	1	4	6	2	5	0	3	5
Para los años bisiestos	6	2

Cálculo memorizable

Este método asigna un número al siglo, el año, el mes y el día. Sumando los cuatro números se obtiene el día de la semana. También puede utilizar este método para hacer cálculos inversos: ¿qué meses contienen un viernes 13? ¿En cuántos años se encontrarán las mismas fechas?

Todos estos números están definidos en módulo 7, es decir, 5 equivale a 12, 19, 26... El resultado final de la suma da el día de la semana, al dar al lunes el número 1. Un resultado final de 12 o -2 corresponderá por tanto a 5, es decir, al viernes.

Este método está basado en el calendario perpetuo de G.D. Moret.[8]​[9]​

El calendario perpetuo de Moret consiste en una serie de tres tablas en las que se puede escribir sucesivamente el siglo, el año, el mes y el día del mes. Se obtiene un nombre del 1 al 7 que corresponde al día de la semana.

Calendarios perpetuos históricos

En 1741 se realizó un calendario perpetuo para el rey francés Luis XV. Consta de cuatro paneles de bronce dorado al mercurio y tiene paneles móviles de esmalte blanco con fechas. Cada panel tiene un cimacio con la insignia real y esta inscripciónː «Almanch perpétuel et toujours nouveau dédié au Roi». A ambos lados de la inscripción están el sol y la luna pintados en oro. Cada panel está dividido verticalmente en tres partes, una por cada mes del trimestre. Cada parte está dividida a su vez en tres columnas, provistas de espigas deslizantes esmaltadasː en la primera columna están los días de la semana y las fases de la luna; en la segunda, la fecha en cifras; en la tercera, los días festivos, junto con el signo zodiacal en esmalte y color y el nombre del mes en blanco y negro. El desplazamiento de las espigas permite ajustar las fechas cada año.[10]​

Otro ejemplo temprano de calendario perpetuo de uso práctico se encuentra en el Nürnberger Handschrift GNM 3227a. El calendario cubre el periodo de 1390-1495 (por lo que el manuscrito está fechado hacia 1389). Para cada año de este periodo, enumera el número de semanas entre el día de Navidad y la Quinquagesima. Se trata del primer caso conocido de una forma tabular de calendario perpetuo que permite el cálculo de las fiestas móviles, que se hicieron populares durante el siglo XV.[5]​

Tablas de los calendarios juliano perpetuo y gregoriano

Tabla uno (cyd)

El siguiente calendario funciona para cualquier fecha a partir del 15 de octubre de 1582, pero sólo para fechas del calendario gregoriano.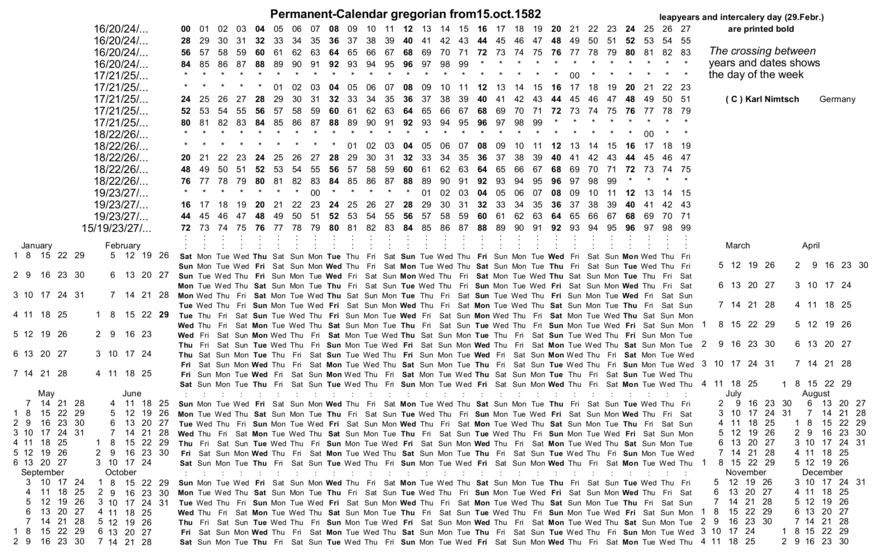

Un auténtico calendario perpetuo, que permite a su usuario buscar el día de la semana para cualquier fecha gregoriana

.

							años del siglo							Ejemplo 1 Gregoriano 31 de marzo de 2006: Greg siglo 20(c) y año 06(y) se encuentran en A en la tabla de Cuadrado latino. La A en la fila Mar(m) se encuentra con 31(d) en Fri en la tabla de Días de la semana. El día es viernes. Ejemplo 2 BC 1 Enero 45: BC 45 = -44 = -100 + 56 (un año bisiesto). -1 y 56 se encuentran en B y Jan_B se encuentra con 1 en Fri(day). Ejemplo 3 Julian 1 Enero 1900: Juliano 19 se reúne a las 00 en A y Jan_A se reúne a las 1 en Sat(urday). Ejemplo 4 Gregorian 1 January 1900: Gregoriano 19 se reúne a las 00 en G y Jan_G se reúne a las 1 en Mon(day).
							00	01	02	03		04	05
							06	07		08	09	10	11
								12	13	14	15		16
							17	18	19		20	21	22
							23		24	25	26	27
							28	29	30	31		32	33
							34	35		36	37	38	39
								40	41	42	43		44
							45	46	47		48	49	50
							51		52	53	54	55
							56	57	58	59		60	61
							62	63		64	65	66	67
								68	69	70	71		72
							73	74	75		76	77	78
							79		80	81	82	83
							84	85	86	87		88	89
							90	91		92	93	94	95
								96	97	98	99
Siglos							Cuadrado latino								Mes
Juliano				Gregoriano
-4	3	10	17	—	—		F	E	D	C	B	A	G		Jan		Apr	Jul
-3	4	11	18	15	19		G	F	E	D	C	B	A		Jan				Oct
-2	5	12	19	16	20		A	G	F	E	D	C	B				May
-1	6	13	20	—	—		B	A	G	F	E	D	C		Feb			Aug
0	7	14	21	17	21		C	B	A	G	F	E	D		Feb	Mar			Nov
1	8	15	22	—	—		D	C	B	A	G	F	E				Jun
2	9	16	23	18	22		E	D	C	B	A	G	F					Sep	Dec
	Dias						Días de la semana
	1	8	15	22	29		Mon	Tue	Wed	Thu	Fri	Sat	Sun
	2	9	16	23	30		Tue	Wed	Thu	Fri	Sat	Sun	Mon
	3	10	17	24	31		Wed	Thu	Fri	Sat	Sun	Mon	Tue
	4	11	18	25			Thu	Fri	Sat	Sun	Mon	Tue	Wed
	5	12	19	26			Fri	Sat	Sun	Mon	Tue	Wed	Thu
	6	13	20	27			Sat	Sun	Mon	Tue	Wed	Thu	Fri
	7	14	21	28			Sun	Mon	Tue	Wed	Thu	Fri	Sat

Siglos Julianos	Siglos Gregoriano		Días de la semana								Meses						Dias
04 11 18	19 23 27		Sun	Mon	Tue	Wed	Thu	Fri	Sat		Jan	Apri	Jul				01	08	15	22	29
03 10 17			Mon	Tue	Wed	Thu	Fri	Sat	Sun					Sep	Dec		02	09	16	23	30
02 09 16	18 22 26		Tue	Wed	Thu	Fri	Sat	Sun	Mon				Jun				03	10	17	24	31
01 08 15			Wed	Thu	Fri	Sat	Sun	Mon	Tue		Feb	Mar			Nov		04	11	18	25
00 07 14	17 21 25		Thu	Fri	Sat	Sun	Mon	Tue	Wed		Feb			Aug			05	12	19	26
–1 06 13			Fri	Sat	Sun	Mon	Tue	Wed	Thu				May				06	13	20	27
–2 05 12	16 20 24		Sat	Sun	Mon	Tue	Wed	Thu	Fri		Jan				Oct		07	14	21	28
Años			00	01	02	03		04	05
			06	07		08	09	10	11
				12	13	14	15		16
			17	18	19		20	21	22
			23		24	25	26	27
			28	29	30	31		32	33
			34	35		36	37	38	39
				40	41	42	43		44
			45	46	47		48	49	50
			51		52	53	54	55
			56	57	58	59		60	61
			62	63		64	65	66	67
				68	69	70	71		72
			73	74	75		76	77	78
			79		80	81	82	83
			84	85	86	87		88	89
			90	91		92	93	94	95
				96	97	98	99

Tabla dos (cymd)

Véase también

• Calendario fijo internacional
• Calendario gregoriano
• Calendario juliano
• Calendario Mundial
• Calendario fijo internacional
• Cálculo del día de la semana
• Era del calendario
• Long Now Foundation
• Regla del fin del mundo

Enlaces externos

• Calendario perpetuo en Excel desde 1900 a 9999
• Sliding Perpetual Calendar on one sheet of paper (U.S. version, PDF)
• Calendario perpetuo deslizante en una hoja de papel (versión no estadounidense, PDF)
• Calendario cónico o piramidal de un año (con tabla del "primero de marzo", PDF)
• Calendario Perpetuo para cualquier año
• Calendario perpetuo en JavaScript
• Perpetual Calendar

Referencias

1. Patente USPTO n.º 1042337, "Calendario (Fred P. Gorin)".
2. Patente USPTO n.º 248872, "Calendario (Robert McCurdy)".
3. «Calendario perpetuo de aluminio». 17 de septiembre de 2011. 
4. Doerfler, Ronald W (29 de agosto de 2019). «Un calendario de "computación gráfica" de 2010». Consultado el 30 de agosto de 2019. 
5. Trude Ehlert, Rainer Leng, Frühe Koch- und Pulverrezepte aus der Nürnberger Handschrift GNM 3227a (um 1389); in: Medizin in Geschichte, Philologie und Ethnologie (2003), p. 291.
6. «Mecanismo del reloj con calendario perpetuo». 17 de septiembre de 2011. 
7. «El misterio del calendario perpetuo de Noguera de Albarracín». Consultado el 5 de septiembre de 2023. 
8. «Calendrier perpétuel» (en francés). Consultado el 13 de noviembre de 2022. 
9. «Le calendrier perpétuel Moret» (en francés). Consultado el 13 de noviembre de 2022. 
10. Bedel, Jean (1991). Dizionario dell'antiquariato : maggiore e minore (en italiano). ISBN 9788876055805. 

Lista de calendarios

Tipos de años gregorianos por ciclo bisiesto por letra dominical (DL) y algoritmo Doomsday (DD)[1]​

Comienzo de año				Años comunes						Años bisiestos
1 ene.	Conteo	Razón		31 dic.	DL	DD	Conteo	Razón		31 dic.	DL	DD	Conteo	Razón
Domingo (D)	58	14.50 %		D	A	M	43	10.75 %		L	AG	X	15	03.75 %
Sábado (S)	56	14.00 %		S	B	L	43	10.75 %		D	BA	M	13	03.25 %
Viernes (V)	58	14.50 %		V	C	D	43	10.75 %		S	CB	L	15	03.75 %
Jueves (J)	57	14.25 %		J	D	S	44	11.00 %		V	DC	D	13	03.25 %
Miércoles (X)	57	14.25 %		X	E	V	43	10.75 %		J	ED	S	14	03.50 %
Martes (M)	58	14.50 %		M	F	J	44	11.00 %		X	FE	V	14	03.50 %
Lunes (L)	56	14.00 %		L	G	X	43	10.75 %		M	GF	J	13	03.25 %
${\displaystyle \Sigma }$	400	100.0 %					303	75.75 %					97	24.25 %

• Datos: Q1383171
• Multimedia: Perpetual calendars / Q1383171
• Libros y manuales: Calendario perpetuo

1. Robert van Gent (2017). «The Mathematics of the ISO 8601 Calendar» (en inglés). Utrecht University, Department of Mathematics. Consultado el 20 de julio de 2017.