|
Análisis del árbol de fallasEl análisis del árbol de fallas (en inglés: Fault tree analysis, FTA) es un análisis de falla deductivo de arriba hacia abajo (descendente) en el que se analiza un estado no deseado de un sistema utilizando la lógica booleana para conjugar una serie de eventos de bajo nivel. Este método de análisis se utiliza sobre todo en los campos de ingeniería de seguridad e ingeniería de fiabilidad para comprender cómo los sistemas pueden fallar, para identificar las mejores formas de reducir un riesgo o para determinar (o comenzar a comprender) tasas de eventos de un accidente de seguridad o una falla (funcional) de un nivel en particular de un sistema. El FTA se aplica en la industria aeroespacial,[1] en la ingeniería nuclear, en la industria de química y procesos,[2][3][4] en la industria farmacéutica,[5] en la industria petroquímica y en otras industrias de alto riesgo; pero también se aplica en campos tan diversos como la identificación de factores de riesgo relacionados con el sistema de fallo del servicio social,[6] lo mismo que en la ingeniería de software, para propósitos de depuración. Está estrechamente relacionado con la técnica de eliminación de causas utilizada para detectar errores de código.[7] En la industria aeroespacial, el término general condición de falla del sistema se usa para el estado no deseado o estado superior del árbol de falla. Estas condiciones se clasifican en función de la severidad de sus efectos. Las condiciones más graves requieren el análisis más extenso del árbol de fallas.[cita requerida] UsoEl análisis de un árbol de fallas puede usarse para:
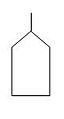
HistoriaEl Análisis del Árbol de Fallas (FTA) fue originalmente desarrollado entre los años 1970 a 1971 en los Laboratorios Bell por H. A. Watson, bajo un contrato con la División de Sistemas de Balística de la Fuerza Aérea de Estados Unidos para evaluar el Sistema de Control de Lanzamiento del Misil Balístico Intercontinental Minuteman I (ICBM).[8][9][10][11] El uso de árboles de fallas desde entonces ha ganado un apoyo extendido y es a menudo utilizado como herramienta de análisis de fallas por expertos en fiabilidad.[12] Siguiendo el primer uso publicado del FTA en el Estudio del Sistema de Control de Lanzamiento del Minuteman I en 1962, Boeing y AVCO expandieron el uso del FTA al sistema completo del Minuteman II en los años 1963-1964. El FTA recibió extensa cobertura en un Simposio de Seguridad de Sistemas en Seattle en 1965, patrocinado por Boeing y la Universidad de Washington.[13] Boeing empezó a utilizar el FTA para el diseño de aeronaves civiles alrededor de 1966.[14][15] Posteriormente, dentro del ejército de EE. UU., la aplicación del FTA para su uso con fuzes fue explorado por el "Picatinny Arsenal" en las décadas de los 60 y 70.[16] En 1976 el Comando de Material Bélico del Ejército de Estados Unidos, incorporó el FTA en un Manual de Diseño de Ingeniería sobre Diseño para Confiabilidad.[17] El Centro de Análisis de la Fiabilidad en el Laboratorio de Roma y sus organizaciones sucesoras, ahora con el Centro de Información Técnica de Defensa (Centro de Análisis de Información de Confiabilidad y ahora Centro de Análisis de Información de Sistemas de Defensa, https://www.dsiac.org/) ha publicado documentación sobre el FTA y los bloques de diagramas de fiabilidad desde la década de los 60.[18][19][20] MIL-HDBK-338B proporciona una referencia más reciente.[21] En 1970, la Administración de Aviación Federal (FAA por sus siglas en inglés) de los EE.UU publicó un cambio respecto a las regulaciones de navegabilidad 14 CFR 25.1309 para aeronaves de categoría de transporte en el Registro Federal en el 35 FR 5665 (1970-04-08). Este cambio adoptó criterios probabilísticos de falla para sistemas de aeronaves y equipamientos, y condujo al amplio uso del FTA en la aviación civil. En 1998, la Administración de Aviación Federal publicó la Orden 8040.4,[22] estableciendo la política de administración de riesgo, que incluye al análisis de riesgo en una gama de actividades críticas más allá de la certificación de aeronaves, incluyendo el control de tráfico aéreo y la modernización del Sistema Nacional de Espacio Aéreo de los EE.UU. Esto condujo a la publicación del Manual de Seguridad del Sistema de la Administración de Aviación Federal, el cual describe el uso del FTA en varios tipos de análisis formales de riesgo.[23] Anteriormente en el proyecto Apolo la cuestión se enmarcaba en la probabilidad de enviar con éxito los astronautas a la Luna y regresarlos a salvo a la Tierra. Se hizo un cálculo de riesgo o fiabilidad de algún tipo, y el resultado fue una probabilidad de éxito de la misión que era inaceptablemente bajo. Este resultado desanimó a la NASA de realizar análisis cuantitativos de riesgo y fiabilidad hasta después del accidente del Challenger en 1986. En cambio, la NASA decidió confiar en el uso del análisis modal de fallos y efectos (AMFE) y otros métodos cualitativos para valoraciones de la seguridad de los sistemas. Después del accidente del Challenger, la importancia de la Evaluación probabilística del riesgo (en inglés: Probabilistic Risk Assessment, PRA) y el FTA en el análisis de riesgo y fiabilidad de sistemas, fueron tomadas en cuenta y empezó a crecer su uso en la NASA, y ahora el FTA es considerado como una de las más importantes técnicas de fiabilidad y análisis de seguridad de sistemas.[24] Dentro de la industria nuclear, La Comisión Reguladora Nuclear de EE. UU. (en inglés: Nuclear Regulatory Commission, NRC) empezó utilizar los métodos de evaluación probabilística del riesgo (en inglés: probabilistic risk assessment, PRA) incluyendo el FTA en 1975, y expandieron significativamente la investigación PRA luego del Accidente de Three Mile Island en 1979.[25] Esto finalmente condujo a la publicación del Manual del Árbol de Fallas NRC NUREG–0492,[26] y al uso obligatorio del PRA bajo autoridad reguladora de la NRC. Luego de desastres de procesos industriales como el Desastre de Bhopal en 1984 y la explosión del Piper Alfa en 1988, en 1992 el Departamento de Seguridad Laboral y Administración de Salud de los EE.UU (en inglés: Occupational Safety and Health Administration, OSHA) publicó en el Registro Federal en el 57 FR 6356 (1992-02-24) su estándar de Administración de Seguridad de Procesos (en inglés: Process Safety Management, PSM) en el 19 CFR 1910.119.[27] OSHA PSM reconoce al FTA como un método aceptable para el análisis de riesgo de procesos. Hoy el FTA es ampliamente utilizado en seguridad de sistemas e ingeniería de fiabilidad, y en todos los campos importantes de la ingeniería. MetodologíaLa metodología del FTA está descrita en varios estándares industriales y del gobierno, incluyendo la NRC NUREG–0492 para la industria nuclear, una revisión del NUREG–0492 orientada a la industria aeroespacial usada por la NASA,[28] la SAE ARP4761 para aeronaves civiles, la MIL–HDBK–338 para sistemas militares, y el estándar IEC IEC 61025[29] que se pretende para el uso de la industria cruzada y ha sido adoptada como Norma europea EN 61025. Cualquier sistema suficientemente complejo está sujeto a fallas, a causa del fallo de uno o más sus subsistemas. La probabilidad de falla, sin embargo, a menudo puede ser reducida a través del diseño mejorado del sistema. El análisis de árboles de fallas mapea la relación entre las fallas, los subsistemas, y los elementos redundantes del diseño de seguridad, creando un esquema lógico del sistema global. El resultado no deseado se toma como la raíz ('acontecimiento / evento superior') de un árbol lógico. Por ejemplo, el resultado no deseado de una operación de prensado y estampado de metal, es que algún apéndice humano sea estampado. Trabajando hacia atrás desde este evento superior, podríamos determinar que hay dos maneras en que esto podría ocurrir: durante una operación normal o durante una operación de mantenimiento. Esta condición es un O lógico. Considerando la rama en la que ocurre durante una operación normal quizás determinamos que hay dos formas en que esto podría pasar: los ciclos de prensa hacen daño el operador o los ciclos de prensa hacen daño a otra persona. Esto es otro O lógico. Podemos hacer una mejora del diseño al requerir que el operador pulse dos botones para echar andar a la máquina - esta es una característica de seguridad en la forma de un Y lógico -. El botón puede tener una taza de fallo intrínseca - esto deviene en un incentivo de falla que podemos analizar-. Cuándo los árboles de fallas son ponderados con números reales para las probabilidades de fallas, los programas computacionales pueden calcular las probabilidades de fracaso en los árboles de fallas. Cuándo se tiene que un acontecimiento en concreto afecta a más de un evento, i.e. tiene impacto en varios subsistemas, se le llama una causa común o modo común. Hablando gráficamente, esto significa que este acontecimiento aparecerá en varias posiciones del árbol. Las causas comunes introducen relaciones de dependencia entre acontecimientos. Los cálculos de probabilidades de un árbol que contiene algunas "causas comunes" son mucho más complicados que en árboles normales donde todos los acontecimientos son considerados como independientes. No todas las herramientas de software disponibles en el mercado proporcionan tal capacidad. El Árbol es normalmente escrito utilizando símbolos convencionales de puertas lógicas. La ruta a través de un árbol entre un acontecimiento y un iniciador en el árbol se llama un Cut Set. La manera creíble más corta a través del árbol desde un fallo hasta un evento inicializador se llama Cut Set Mínimo. Algunas industrias utilizan ambos: los árboles de falla y los árboles de eventos (ver Valoración de Riesgo Probabilística). Un Árbol de Eventos empieza desde un inicializador no deseado (pérdida de suministro crítico, fracaso de componente, etc.) y sigue posibles eventos más lejanos del sistema a través de una serie de consecuencias finales. A medida que cada acontecimiento nuevo es considerado, se añade un nuevo nodo al árbol con una probabilidad dividida de tomar cualquier rama. Las probabilidades de una gama de 'acontecimientos superiores' surgiendo del acontecimiento inicial entonces pueden verse. Los programas clásicos incluyen el software (EPRI) CAFTA del Instituto de Investigación de Energía Eléctrica, el cual es utilizado por muchas de los plantas nucleares de EE. UU. y por la mayoría de los fabricantes aeroespaciales internacionales y de EE. UU., y el SAPHIRE del Laboratorio Nacional de Idaho, el cual es utilizado por el Gobierno de EE. UU. para evaluar la seguridad y fiabilidad de reactores nucleares, el Transbordador espacial, y la Estación Espacial Internacional. Fuera de los EE. UU., el software RiskSpectrum es una herramienta popular para los análisis de Árbol de Fallas y de Árbol de Eventos y está autorizado para su uso en casi la mitad de las plantas nucleares del mundo por Evaluación Probabilística de Seguridad. Símbolos gráficosLos símbolos básicos utilizados en el FTA están agrupados como eventos, puertas, y símbolos de transferencia. Variaciones menores pueden ser utilizadas en softwares de FTA. Símbolos de los eventosLos símbolos de eventos son utilizados para acontecimientos primarios y acontecimientos intermedios. Los eventos primarios no se desarrollan más en el árbol de fallas. Los acontecimientos intermedios se encuentran en la salida de una puerta. Los símbolos de eventos se muestran debajo:
Los símbolos de eventos primarios son típicamente utilizados como sigue:
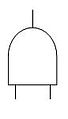
Una puerta de evento intermedio se puede utilizar inmediatamente por encima de un evento primario, para proporcionar más espacio para escribir la descripción del evento. El FTA es un enfoque de arriba hacia abajo (descendente). Símbolos de puerta lógicaLos símbolos de puerta describen la relación entre los eventos de entrada y de salida. Los símbolos se derivan de símbolos lógicos booleanos:
Las puertas funcionan como sigue:
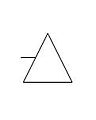
Símbolos de transferenciaLos símbolos de transferencia son usados para conectar las entradas y las salidas de árboles de fallas relacionados, tal como el árbol de fallas de un subsistema al de su sistema. La NASA preparó una documentación completa sobre el FTA a través de incidentes prácticos.
Fundamentación matemática básicaLos eventos en un árbol de fallas están asociados con probabilidades estadísticas. Por ejemplo, las componentes fallidas pueden presentarse generalmente con algún índice de falla constante λ (una función de riesgo constante). En este caso más sencillo, la probabilidad de falla depende del índice λ y del tiempo de exposición t:
Un árbol de fallas suele normalizarse a un intervalo de tiempo dado, como una hora de vuelo o un tiempo de misión mediano. Las probabilidades de los eventos dependen de la relación entre la función de riesgo del evento y su intervalo.[cita requerida] A diferencia de los esquemas de puertas lógicas convencionales en los cuales las entradas y las salidas contienen los valores binarios de CIERTOS (1) o FALSOS (0), las puertas en el árbol de fallas producen probabilidades relacionadas con las operaciones de conjunto de la lógica Booleana. La probabilidad del evento de salida de una puerta depende de las probabilidades de los eventos de la entrada. Una puerta de Y lógico representa una combinación de acontecimientos independientes. Esto es, la probabilidad de cualquier acontecimiento de entrada a una puerta de Y lógico no se ve afectada por ningún otro acontecimiento de entrada a la misma puerta. En términos de teoría de conjuntos, esto es equivalente a la intersección de los conjuntos de eventos de la entrada, y la probabilidad de la salida de la puerta de Y lógico está dada por:
Una puerta de O lógico, por otro lado, corresponde a una unión de conjuntos:
Como las probabilidades de fallas en árboles de fallas tienden a ser pequeñas (menos de .01), P (A ∩ B) normalmente deviene en un término de error muy pequeño, y la salida de una puerta de O lógico puede ser aproximada conservadoramente usando la suposición de que las entradas son eventos mutuamente excluyentes:
La puerta de O-Exclusivo con dos entradas representa la probabilidad que una o la otra entrada, pero no ambas, ocurra:
Nuevamente, como P (A ∩ B) normalmente deviene en un término de error muy pequeño, la puerta de O-Exclusivo tiene valor limitado en un árbol de fallas. AnálisisMuchas aproximaciones diferentes se pueden usar para modelar un FTA, pero la más común y popular puede ser resumida en unos cuantos pasos. Un único árbol de fallas se usa para analizar uno y sólo un evento no deseado o evento superior, el cual puede alimentar posteriormente a otro árbol de falla como un evento básico. Aunque la naturaleza del evento no deseado puede variar dramáticamente, un FTA sigue el mismo procedimiento para cualquier evento no deseado; sea un retraso de 0.25 ms en la generación de energía eléctrica, un incendio no detectado en una bodega, o el lanzamiento fortuito e involuntario de un ICBM. Debido al costo de mano de obra, el FTA sólo se utiliza normalmente para eventos no deseados más graves. El FTA implica cinco pasos:
Comparación con otros métodos analíticosEl FTA es un método deductivo, descendente, dirigido a analizar los efectos de iniciar fallas y eventos en un sistema complejo. Esto contrasta con el análisis modal de fallos y efectos (FMEA), que es un método inductivo de análisis bottom-up que tiene como objetivo analizar los efectos de fallas de un solo componente o función en equipos o subsistemas. El FTA es muy bueno para mostrar cuán resistente es un sistema a fallas simples o múltiples. No es bueno para encontrar todas las posibles fallas iniciales. El FMEA es bueno en catalogar de forma exhaustiva las fallas iniciales, y en la identificación de sus efectos locales. No es bueno para examinar los fallos múltiples o sus efectos a nivel del sistema. El FTA considera los eventos externos, el FMEA no. En la aeronáutica civil la práctica habitual es realizar tanto FTA y FMEA, con un resumen de efectos de modo de fallo (FMES) como la interfaz entre el FMEA y el FTA. Las alternativas al FTA incluyen los diagramas de dependencias (DD), también conocidos como diagramas de bloques de fiabilidad (RBD) y el análisis de Markov. Un diagrama de dependencias es equivalente a un análisis de árbol de éxito (en inglés: Success Tree Analysis, STA), el inverso lógico de un FTA, y representa el sistema utilizando rutas en lugar de puertas. DD y STA producen probabilidades de éxito (es decir, evitar un evento superior) en lugar de la probabilidad de un evento superior. Véase también
Referencias
|
Portal di Ensiklopedia Dunia