|
User talk:Crowsnest
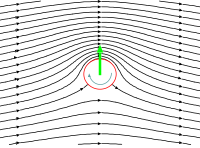
Lifting flow around a circular cylinderHello Crowsnest. You produced the excellent diagram with the caption “Streamlines for the incompressible potential flow around a circular cylinder in a uniform onflow.” It is available at Potential flow#Description and characteristics. It shows flow with circulation of zero. There is a need for a similar diagram but with a non-zero circulation. Such a diagram could be applied at Magnus effect and Kutta–Joukowski theorem. The symmetry of the streamlines about a vertical axis through the centre of the cylinder would be helpful in demonstrating that in two-dimensional flow the upwash upstream of a cylinder is a mirror image of the downwash downstream of the cylinder. It would also help demonstrate that there is no lift-induced drag in two-dimensional flow about an airfoil. The diagram I have in mind is often used in text books and websites. For example, the one by Prof Richard Fitzpatrick (University of Texas) shown at the following website: Flow Past a Cylindrical Obstacle Are you able to produce such a diagram for use on Wikipedia? Dolphin (t) 12:35, 30 March 2024 (UTC)
ArbCom 2024 Elections voter messageHello! Voting in the 2024 Arbitration Committee elections is now open until 23:59 (UTC) on Monday, 2 December 2024. All eligible users are allowed to vote. Users with alternate accounts may only vote once. The Arbitration Committee is the panel of editors responsible for conducting the Wikipedia arbitration process. It has the authority to impose binding solutions to disputes between editors, primarily for serious conduct disputes the community has been unable to resolve. This includes the authority to impose site bans, topic bans, editing restrictions, and other measures needed to maintain our editing environment. The arbitration policy describes the Committee's roles and responsibilities in greater detail. If you wish to participate in the 2024 election, please review the candidates and submit your choices on the voting page. If you no longer wish to receive these messages, you may add |
Portal di Ensiklopedia Dunia