Square root of 3

Square root of 3

The height of an equilateral triangle with sides of length 2 equals the square root of 3.
Representations
Decimal	1.7320508075688772935...
Continued fraction	${\displaystyle 1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+\ddots }}}}}}}}}}}$

The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is denoted mathematically as ${\textstyle {\sqrt {3}}}$ or ${\displaystyle 3^{1/2}}$. It is more precisely called the principal square root of 3 to distinguish it from the negative number with the same property. The square root of 3 is an irrational number. It is also known as Theodorus' constant, after Theodorus of Cyrene, who proved its irrationality.^[citation needed]

In 2013, its numerical value in decimal notation was computed to ten billion digits.[1] Its decimal expansion, written here to 65 decimal places, is given by OEIS: A002194:

1.732050807568877293527446341505872366942805253810380628055806

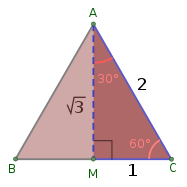
The fraction ${\textstyle {\frac {97}{56}}}$ (1.732142857...) can be used as a good approximation. Despite having a denominator of only 56, it differs from the correct value by less than ${\textstyle {\frac {1}{10,000}}}$ (approximately ${\textstyle 9.2\times 10^{-5}}$, with a relative error of ${\textstyle 5\times 10^{-5}}$). The rounded value of 1.732 is correct to within 0.01% of the actual value.^[citation needed]

The fraction ${\textstyle {\frac {716,035}{413,403}}}$ (1.73205080756...) is accurate to ${\textstyle 1\times 10^{-11}}$.^[citation needed]

Archimedes reported a range for its value: ${\textstyle ({\frac {1351}{780}})^{2}>3>({\frac {265}{153}})^{2}}$.[2]

The lower limit ${\textstyle {\frac {1351}{780}}}$ is an accurate approximation for ${\displaystyle {\sqrt {3}}}$ to ${\textstyle {\frac {1}{608,400}}}$ (six decimal places, relative error ${\textstyle 3\times 10^{-7}}$) and the upper limit ${\textstyle {\frac {265}{153}}}$ to ${\textstyle {\frac {2}{23,409}}}$ (four decimal places, relative error ${\textstyle 1\times 10^{-5}}$).

Expressions

It can be expressed as the simple continued fraction [1; 1, 2, 1, 2, 1, 2, 1, …] (sequence A040001 in the OEIS).

So it is true to say:

${\displaystyle {\begin{bmatrix}1&2\\1&3\end{bmatrix}}^{n}={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}}$

then when ${\displaystyle n\to \infty }$ :

${\displaystyle {\sqrt {3}}=2\cdot {\frac {a_{22}}{a_{12}}}-1}$

Geometry and trigonometry

The height of an equilateral triangle with edge length 2 is √3. Also, the long leg of a 30-60-90 triangle with hypotenuse 2.

And, the height of a regular hexagon with sides of length 1.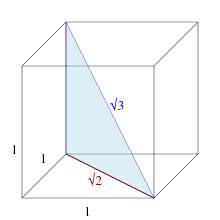

The space diagonal of the unit cube is √3.

Distances between vertices of a double unit cube are square roots of the first six natural numbers, including the square root of 3 (√7 is not possible due to Legendre's three-square theorem)

This projection of the Bilinski dodecahedron is a rhombus with diagonal ratio √3.

The square root of 3 can be found as the leg length of an equilateral triangle that encompasses a circle with a diameter of 1.

If an equilateral triangle with sides of length 1 is cut into two equal halves, by bisecting an internal angle across to make a right angle with one side, the right angle triangle's hypotenuse is length one, and the sides are of length ${\textstyle {\frac {1}{2}}}$ and ${\textstyle {\frac {\sqrt {3}}{2}}}$. From this, ${\textstyle \tan {60^{\circ }}={\sqrt {3}}}$, ${\textstyle \sin {60^{\circ }}={\frac {\sqrt {3}}{2}}}$, and ${\textstyle \cos {30^{\circ }}={\frac {\sqrt {3}}{2}}}$.

The square root of 3 also appears in algebraic expressions for various other trigonometric constants, including[3] the sines of 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84°, and 87°.

It is the distance between parallel sides of a regular hexagon with sides of length 1.

It is the length of the space diagonal of a unit cube.

The vesica piscis has a major axis to minor axis ratio equal to ${\displaystyle 1:{\sqrt {3}}}$. This can be shown by constructing two equilateral triangles within it.

Other uses and occurrence

Power engineering

In power engineering, the voltage between two phases in a three-phase system equals ${\textstyle {\sqrt {3}}}$ times the line to neutral voltage. This is because any two phases are 120° apart, and two points on a circle 120 degrees apart are separated by ${\textstyle {\sqrt {3}}}$ times the radius (see geometry examples above).^[citation needed]

Special functions

It is known that most roots of the nth derivatives of ${\displaystyle J_{\nu }^{(n)}(x)}$ (where n < 18 and ${\displaystyle J_{\nu }(x)}$ is the Bessel function of the first kind of order ${\displaystyle \nu }$) are transcendental. The only exceptions are the numbers ${\displaystyle \pm {\sqrt {3}}}$, which are the algebraic roots of both ${\displaystyle J_{1}^{(3)}(x)}$ and ${\displaystyle J_{0}^{(4)}(x)}$. [4]^[clarification needed]

References

1. Komsta, Łukasz (December 2013). "Computations | Łukasz Komsta". komsta.net. WordPress. Archived from the original on 2023-10-02. Retrieved September 24, 2016.
2. Knorr, Wilbur R. (June 1976). "Archimedes and the measurement of the circle: a new interpretation". Archive for History of Exact Sciences. 15 (2): 115–140. doi:10.1007/bf00348496. JSTOR 41133444. MR 0497462. S2CID 120954547. Retrieved November 15, 2022 – via SpringerLink.
3. Wiseman, Julian D. A. (June 2008). "Sin and Cos in Surds". JDAWiseman.com. Retrieved November 15, 2022.
4. Lorch, Lee; Muldoon, Martin E. (1995). "Transcendentality of zeros of higher dereivatives of functions involving Bessel functions". International Journal of Mathematics and Mathematical Sciences. 18 (3): 551–560. doi:10.1155/S0161171295000706.

• Podestá, Ricardo A. (2020). "A geometric proof that sqrt 3, sqrt 5, and sqrt 7 are irrational". arXiv:2003.06627 [math.GM].

Further reading

• The review of: Jones, M. F. (1968). "22900D approximations to the square roots of the primes less than 100". Mathematics of Computation. 22 (101): 234–235. doi:10.2307/2004806. JSTOR 2004806.
• Uhler, H. S. (1951). "Approximations exceeding 1300 decimals for ${\displaystyle {\sqrt {3}}}$, ${\displaystyle {\frac {1}{\sqrt {3}}}}$, ${\displaystyle \sin({\frac {\pi }{3}})}$ and distribution of digits in them". Proc. Natl. Acad. Sci. U.S.A. 37 (7): 443–447. doi:10.1073/pnas.37.7.443. PMC 1063398. PMID 16578382.
• Wells, D. (1997). The Penguin Dictionary of Curious and Interesting Numbers (Revised ed.). London: Penguin Group. p. 23.

External links

• Theodorus' Constant at MathWorld
• Kevin Brown, Archimedes and the Square Root of 3