|
Scaphe The scaphe (Ancient Greek: σκάφη, romanized: scaphe, lit. 'bowl'; also known as a skaphe, scaphion (diminutive) or Latin: scaphium) was a sundial said to have been invented by Aristarchus of Samos (3rd century BC). There are no original works still in existence by Aristarchus, but the adjacent picture is an image of what it might have looked like; only his would have been made of stone. It consisted of a hemispherical bowl which had a vertical gnomon placed inside it, with the top of the gnomon level with the edge of the bowl. Twelve gradations inscribed perpendicular to the hemisphere indicated the hour of the day. InventorAristarchus of Samos (/ˌærəˈstɑːrkəs/; Ἀρίσταρχος, Aristarkhos; c. 310 – c. 230 BC) was an ancient Greek astronomer and mathematician who presented the first known model that placed the Sun at the center of the known universe with the Earth revolving around it (see Solar System). He was influenced by Philolaus of Croton, but he identified the "central fire" with the Sun, and put the other planets in their correct order of distance around the Sun.[1] His astronomical ideas were often rejected in favor of the geocentric theories of Aristotle and Ptolemy. History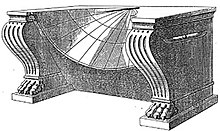 Greeks and Romans used large stone sundials based on "a partial sphere or scaphe,” the shadow of the tip of the gnomon was the time-telling index.[2] These dials could in theory tell time accurately if carved to a true sphere and correctly calibrated for a given site.  It took a skilled stone worker and a great deal of time and money to create a sundial. So only wealthy citizens could afford this elaborate contraption, and it was often for their villas or as donations for erection in the town forum. There was a need for cheaper dials that ordinary laborer could construct. But even if it were easier to make, the question of calibrating the scaphe still posed a problem. The problem of projecting the three-dimensional scaphe dial upon a vertical or horizontal plane was addressed by a number of distinguished nineteenth-century mathematicians, each of whom presumably solved it to his own personal satisfaction. Unfortunately, their publications are so complex, long-winded, and obscure that they were virtually inaccessible to antiquaries and—it would appear from the replication of effort—even to their own (unacknowledged) colleagues.[2] The spherical trigonometry required for the latter endeavor is really quite basic, and the calculations tedious rather than difficult. The availability of computer-generated graphics has, of course, completely altered the situation. A Fortran program was written for the VAX computer at the University of Leicester that enabled vertical or horizontal dials to be plotted for any latitude.[2] See alsoReferences
Bibliography
External links
|
Portal di Ensiklopedia Dunia