Order-3-4 heptagonal honeycomb

Order-3-4 heptagonal honeycomb
Type	Regular honeycomb
Schläfli symbol	{7,3,4}
Coxeter diagram	=
Cells	{7,3}
Faces	heptagon {7}
Vertex figure	octahedron {3,4}
Dual	{4,3,7}
Coxeter group	[7,3,4]
Properties	Regular

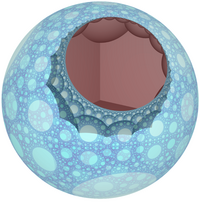
In the geometry of hyperbolic 3-space, the order-3-4 heptagonal honeycomb or 7,3,4 honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.

Geometry

The Schläfli symbol of the order-3-4 heptagonal honeycomb is {7,3,4}, with four heptagonal tilings meeting at each edge. The vertex figure of this honeycomb is an octahedron, {3,4}.

Poincaré disk model (vertex centered)

One hyperideal cell limits to a circle on the ideal surface

Ideal surface

Related polytopes and honeycombs

It is a part of a series of regular polytopes and honeycombs with {p,3,4} Schläfli symbol, and octahedral vertex figures:

{p,3,4} regular honeycombs
Space	S^3	E^3	H^3
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,4}	{4,3,4}	{5,3,4}	{6,3,4}	{7,3,4}	{8,3,4}	... {∞,3,4}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Order-3-4 octagonal honeycomb

Order-3-4 octagonal honeycomb
Type	Regular honeycomb
Schläfli symbol	{8,3,4}
Coxeter diagram	=
Cells	{8,3}
Faces	octagon {8}
Vertex figure	octahedron {3,4}
Dual	{4,3,8}
Coxeter group	[8,3,4] [8,3^1,1]
Properties	Regular

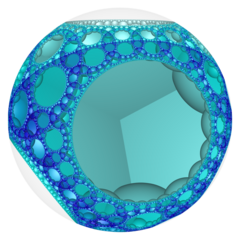
In the geometry of hyperbolic 3-space, the order-3-4 octagonal honeycomb or 8,3,4 honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an octagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.

The Schläfli symbol of the order-3-4 octagonal honeycomb is {8,3,4}, with four octagonal tilings meeting at each edge. The vertex figure of this honeycomb is an octahedron, {3,4}.

Poincaré disk model (vertex centered)

Order-3-4 apeirogonal honeycomb

Order-3-4 apeirogonal honeycomb
Type	Regular honeycomb
Schläfli symbol	{∞,3,4}
Coxeter diagram	=
Cells	{∞,3}
Faces	apeirogon {∞}
Vertex figure	octahedron {3,4}
Dual	{4,3,∞}
Coxeter group	[∞,3,4] [∞,3^1,1]
Properties	Regular

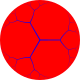
In the geometry of hyperbolic 3-space, the order-3-4 apeirogonal honeycomb or ∞,3,4 honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-3 apeirogonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.

The Schläfli symbol of the order-3-4 apeirogonal honeycomb is {∞,3,4}, with four order-3 apeirogonal tilings meeting at each edge. The vertex figure of this honeycomb is an octahedron, {3,4}.

Poincaré disk model (vertex centered)

Ideal surface

See also

• Convex uniform honeycombs in hyperbolic space
• List of regular polytopes

References

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
• Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I, II)
• George Maxwell, Sphere Packings and Hyperbolic Reflection Groups, JOURNAL OF ALGEBRA 79,78-97 (1982) [1]
• Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, (2013)[2]
• Visualizing Hyperbolic Honeycombs arXiv:1511.02851 Roice Nelson, Henry Segerman (2015)

External links

• John Baez, Visual insights: {7,3,3} Honeycomb (2014/08/01) {7,3,3} Honeycomb Meets Plane at Infinity (2014/08/14)
• Danny Calegari, Kleinian, a tool for visualizing Kleinian groups, Geometry and the Imagination 4 March 2014. [3]