Moufang loop
|
Read other articles:

Kingdom Щ…Щ…Щ„ЩғШ© ЩғШ§ШЁШ§ЩҲЩҶ ШҜЩҲЩҠЩ„Ш© ЩҶШ§ШҙШҰШ© ШЁШ№ШҜ Ш§Щ„Щ…Щ…Щ„ЩғШ© Ш§Щ„Щ…ЩҲШұЩҠШ© Ш§Щ„ШұЩҲЩ…Ш§ЩҶЩҠШ© Rump state, exclave 578вҖ“708 Щ…Щ…Щ„ЩғШ© ЩғШ§ШЁШ§ЩҲЩҶ (8) ЩҲШәЩҠШұЩҮШ§ Щ…ЩҶ Ш§Щ„Щ…Щ…Ш§Щ„Щғ Ш§Щ„ШЁШұШЁШұЩҠШ© ЩҒЩҠ ШЈЩҲШ§Ш®Шұ Ш§Щ„ЩӮШұЩҶ Ш§Щ„ШіШ§ШҜШі. ЩҶШёШ§Щ… Ш§Щ„ШӯЩғЩ… Щ…Щ„ЩғЩҠШ© Ш§Щ„ШҜЩҠШ§ЩҶШ© Щ…ШіЩҠШӯЩҠШ© (Ш§Щ„ЩғЩҶЩҠШіШ© Ш§Щ„ШұЩҲЩ…Ш§ЩҶЩҠШ© Ш§Щ„ЩғШ§Ш«ЩҲЩ„ЩҠЩғЩҠШ©) Ш§Щ„Щ…Щ„Щғ (ШәЩҠШұ Щ…Ш№ШұЩҲЩҒ) 578-708 Ш§Щ„ШӘШ§ШұЩҠШ® Ш§Щ„ЩҒШӘШұШ© Ш§Щ„ШӘШ§ШұЩҠШ®ЩҠШ© Ш§Щ„Ш№ШөЩҲШұ Ш§Щ„ЩҲШіШ·Щү ШҘЩҶЩҮЩҠШ§Ш…

Voce principale: L.R. Vicenza. Associazione del Calcio in VicenzaStagione 1905-1906Sport calcio SquadraVicenza Calcio Allenatore Antonio Libero Scarpa Presidente Antonio Libero Scarpa Terza Categoria1Вә Torneo FGNIFinalista 1904-1905 1906-1907 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Associazione Del Calcio In Vicenza nelle competizioni ufficiali della stagione 1905-1906. Indice 1 Stagione 2 Organigramma societario 3 Rosa 4 Calciomercato 5 Risult…

Indonesian traditional salad dish KulubanCourseSide dishPlace of originJava, IndonesiaRegion or stateCentral Java, YogyakartaCreated byJavanese cuisineServing temperatureMostly served with main courseMain ingredientsSteamed vegetable salad, shredded coconut dressing Kuluban is a traditional[1] salad of Central Java. Kuluban can be consumed on its own as a salad for vegetarian meals or as a side dish. Kuluban is one of ancient Javanese cuisine, as it was mentioned in inscription dated fro…

Canadian actress Laura MennellMennell, photographed in 2009Born (1980-04-18) 18 April 1980 (age 44)[1]Surrey, British Columbia, Canada[1]OccupationActressYears active1996вҖ“presentRelativesAlan Young (cousin) Laura Mennell (/mЙӣЛҲnЙӣl/; born 18 April 1980) is a Canadian actress known for her roles in Thirteen Ghosts, Alphas, Haven, Loudermilk, The Man in the High Castle, Watchmen and Batwoman. In 2011/2012 Mennell co-starred on the Sci-fi television series Alphas. Laura…

РҹРҫСҒРҫР»СҢСҒСӮРІРҫ РҜРҝРҫРҪРёРё РІ Р РҫСҒСҒРёР№СҒРәРҫР№ РӨРөРҙРөСҖР°СҶРёРёСҸРҝ. еңЁгғӯгӮ·гӮўж—Ҙжң¬еӣҪеӨ§дҪҝйӨЁ РҜРҝРҫРҪРёСҸ Р РҫСҒСҒРёСҸ РңРөСҒСӮРҫРҝРҫР»РҫР¶РөРҪРёРө БаСҒРјР°РҪРҪСӢР№ СҖайРҫРҪ, РңРҫСҒРәРІР° РҗРҙСҖРөСҒ Р“СҖРҫС…РҫР»СҢСҒРәРёР№ РҝРөСҖ., 27 РҹРҫСҒРҫР» РҗРәРёСҖР° РңСғСӮРҫ СайСӮ ru.emb-japan.go.jp РңРөРҙиафайлСӢ РҪР° Р’РёРәРёСҒРәлаРҙРө РҹРҫСҒРҫР»СҢСҒСӮРІРҫ РҜРҝРҫРҪРёРё РІ РңРҫСҒРәРІРө (СҸРҝ. еңЁгғӯгӮ·гӮўж—Ҙжң¬еӣҪеӨ§дҪҝйӨЁ) вҖ” РҙРёРҝР»РҫРјР°СӮРёСҮРөСҒРәР°СҸ Р…

Astronomical observatory in Hawaii W. M. Keck ObservatoryThe Keck observatory domes atop Mauna KeaAlternative namesKeck telescope Part ofMauna Kea Observatories Location(s)HawaiiCoordinates19В°49вҖІ35вҖіN 155В°28вҖІ28вҖіW / 19.8263В°N 155.47441В°W / 19.8263; -155.47441 Altitude4,145 m (13,599 ft) First lightNovember 24, 1990 (1990-11-24), October 23, 1996 (1996-10-23)Telescope styleastronomical observatoryreflect…

British Army general Sir James Edward EdmondsNickname(s)ArchimedesBorn25 December 1861London, EnglandDied2 August 1956(1956-08-02) (aged 94)Sherborne, EnglandAllegiance United KingdomService/branchBritish ArmyRankBrigadier-GeneralCommands heldSecret Service Bureau Chief of Staff, 4th Division (1914) Historical Section, Committee of Imperial DefenceBattles/warsSecond Boer WarRusso-Japanese WarFirst World WarAwardsKnight BachelorCompanion of the Order of the BathCompanion of the Order of…

РҘСҖРёСҒСӮРёР°РҪСҒСӮРІРҫБиРұлиСҸ Р’РөСӮС…РёР№ ЗавРөСӮ РқРҫРІСӢР№ ЗавРөСӮ ЕваРҪРіРөлиРө Р”РөСҒСҸСӮСҢ Р·Р°РҝРҫРІРөРҙРөР№ РқагРҫСҖРҪР°СҸ РҝСҖРҫРҝРҫРІРөРҙСҢ РҗРҝРҫРәСҖРёС„СӢ Р‘РҫРі, РўСҖРҫРёСҶР° Р‘РҫРі РһСӮРөСҶ РҳРёСҒСғСҒ РҘСҖРёСҒСӮРҫСҒ РЎРІСҸСӮРҫР№ Р”СғС… РҳСҒСӮРҫСҖРёСҸ С…СҖРёСҒСӮРёР°РҪСҒСӮРІР° РҗРҝРҫСҒСӮРҫР»СӢ РҘСҖРҫРҪРҫР»РҫРіРёСҸ С…СҖРёСҒСӮРёР°РҪСҒСӮРІР° Р Р°РҪРҪРөРө С…СҖРёСҒСӮРёР°РҪСҒСӮРІРҫ Р“РҪРҫСҒСӮРёСҮРөСҒРәРҫРө С…СҖРёСҒСӮРёР°РҪСҒСӮРІРҫ Р’СҒРөР»РөРҪСҒРәРёРө СҒРҫРұРҫСҖСӢ РқРёР…

Charlie Jones NazionalitГ Stati Uniti GenereHeavy metalHard rockRock gotico Periodo di attivitГ musicale1983 вҖ“ in attivitГ Strumentobatteria, chitarra, tastiera elettronica, voce Gruppi attualiCold Chisel Gruppi precedentiThe Cult, The Dead Daisies, Divinyls Modifica dati su Wikidata В· Manuale Charlie Drayton (New York, 9 maggio 1965) ГЁ un batterista, polistrumentista e compositore statunitense, noto per essere stato membro della band The Cult, e per essere il…
2020е№ҙеӨҸеӯЈеҘҘжһ—еҢ№е…ӢиҝҗеҠЁдјҡжіўе…°д»ЈиЎЁеңҳжіўе…°еӣҪж——IOCз·ЁзўјPOLNOCжіўиҳӯеҘ§жһ—еҢ№е…Ӣ委員жңғз¶Із«ҷolimpijski.plпјҲиӢұж–ҮпјүпјҲжіўе…°ж–Үпјү2020е№ҙеӨҸеӯЈеҘҘжһ—еҢ№е…ӢиҝҗеҠЁдјҡпјҲжқұдә¬пјү2021е№ҙ7жңҲ23ж—ҘиҮі8жңҲ8ж—ҘпјҲеҸ—2019еҶ зҠ¶з—…жҜ’з—…з–«жғ…еҪұе“ҚжҺЁиҝҹпјҢдҪҶд»Қдҝқз•ҷеҺҹе®ҡеҗҚз§°пјүйҒӢеӢ•е“Ў206еҸғиіҪй …зӣ®24дёӘеӨ§йЎ№ж——жүӢејҖ幕ејҸпјҡеё•з»ҙ尔·科зғӯе°јеҘҘеӨ«ж–ҜеҹәпјҲжёёжііпјүе’Ң马娅·жІғд»Җд№”еӨ«ж–ҜеҚЎпјҲиҮӘиЎҢиҪҰпјү[1]й—ӯ幕ејҸпјҡеҚЎзҪ—еҲ©еЁңВ·зәідәҡпјҲзҡ®еҲ’иүҮпјү[2…

Delineasi daerah aliran sungai adalah proses pemetaan dan penentuan batas wilayah atau area yang mengalirkan air hujan atau sungai ke satu titik tertentu dalam suatu sungai atau sistem sungai. DAS adalah unit geografis yang mencakup seluruh daerah yang berfungsi sebagai saluran alami bagi air hujan yang jatuh di dalamnya menuju sungai atau saluran air utama yang lebih besar.[1][2] Kegunaan delineasi DAS Kegunaan dari delineasi DAS adalah sebagai berikut:[3][4] Pen…

е…ідәҺдёҺгҖҢе…§й–ЈзёҪзҗҶеӨ§иҮЈгҖҚжЁҷйЎҢзӣёиҝ‘жҲ–зӣёеҗҢзҡ„жқЎзӣ®йЎөпјҢи«ӢиҰӢгҖҢе…§й–ЈзёҪзҗҶеӨ§иҮЈ (ж¶Ҳжӯ§зҫ©)гҖҚгҖӮ ж—Ҙжң¬еңӢе…§й–ЈзёҪзҗҶеӨ§иҮЈе…§й–ЈзёҪзҗҶеӨ§иҮЈзҙӢз« зҸҫд»»еІёз”°ж–Үйӣ„иҮӘ2021е№ҙ10жңҲ4ж—ҘеңЁд»»е°Ҡз§°зёҪзҗҶгҖҒзёҪзҗҶеӨ§иҮЈгҖҒйҰ–зӣёгҖҒйҳҒдёӢе®ҳйӮёзёҪзҗҶеӨ§иҮЈе®ҳйӮёжҸҗеҗҚиҖ…еңӢжңғе…Ёй«”иӯ°е“ЎйҒёеҮәд»»е‘ҪиҖ…еӨ©зҡҮд»»жңҹеӣӣе№ҙпјҢз„ЎйҖЈд»»йҷҗеҲ¶[иЁ» 1]иЁӯз«Ӣжі•жәҗж—Ҙжң¬еңӢжҶІжі•е…ҲеүҚиҒҢдҪҚеӨӘж”ҝеӨ§иҮЈпјҲеӨӘж”ҝе®ҳпјүйҰ–д»»дјҠи—ӨеҚҡж–Үи®ҫз«Ӣ1885е№ҙ12жңҲ22ж—ҘпјҢ…

Galaxy in the constellation Hercules NGC 6158SDSS image of NGC 6158.Observation data (J2000 epoch)ConstellationHerculesRight ascension16h 27m 40.9s[1]Declination39° 22′ 59″[1]Redshift0.029954[1]Heliocentric radial velocity8980 km/s[1]Distance123 Mpc (401 Mly)[1]Group or clusterAbell 2199Apparent magnitude (V)14.68[1]CharacteristicsTypeE?[1]Size~162,000 ly (49.6 kpc)[1] (estimated)&…

ЩҠЩҒШӘЩӮШұ Щ…ШӯШӘЩҲЩү ЩҮШ°ЩҮ Ш§Щ„Щ…ЩӮШ§Щ„Ш© ШҘЩ„Щү Ш§Щ„Ш§ШіШӘШҙЩҮШ§ШҜ ШЁЩ…ШөШ§ШҜШұ. ЩҒШ¶Щ„Ш§ЩӢШҢ ШіШ§ЩҮЩ… ЩҒЩҠ ШӘШ·ЩҲЩҠШұ ЩҮШ°ЩҮ Ш§Щ„Щ…ЩӮШ§Щ„Ш© Щ…ЩҶ Ш®Щ„Ш§Щ„ ШҘШ¶Ш§ЩҒШ© Щ…ШөШ§ШҜШұ Щ…ЩҲШ«ЩҲЩӮ ШЁЩҮШ§. ШЈЩҠ Щ…Ш№Щ„ЩҲЩ…Ш§ШӘ ШәЩҠШұ Щ…ЩҲШ«ЩӮШ© ЩҠЩ…ЩғЩҶ Ш§Щ„ШӘШҙЩғЩҠЩғ ШЁЩҮШ§ ЩҲШҘШІШ§Щ„ШӘЩҮШ§. (Щ…Ш§ШұШі 2016) Ш§Щ„ШЁШ·ЩҲЩ„Ш© Ш§Щ„ЩҶШіШ®Ш© Ш§Щ„ШЈЩҲЩ„Щү Ш§Щ„ЩҶШіШ®Ш© Ш§Щ„ШЈШ®ЩҠШұШ© Ш§Щ„ШЈЩғШ«Шұ ЩҒЩҲШІШ§ЩӢ ШЁШ·ЩҲЩ„Ш§ШӘ ШұШіЩ…ЩҠШ© Ш§Щ„ШҜЩҲШұЩҠ Ш§Щ„Щ…Щ…ШӘШ§ШІ 1961 Щ…ШіШӘЩ…Шұ ЩҶШ§ШҜЩҠ Ш§Щ„ЩӮШ§ШҜШіЩҠШ© (17 Щ…ШұШ©)…

French academic (born 1952) You can help expand this article with text translated from the corresponding article in French. (May 2019) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text in…

American intercollegiate baseball squad Mississippi State Bulldogs baseball 2024 Mississippi State Bulldogs baseball teamFounded1885Overall record2,812вҖ“1,656вҖ“29UniversityMississippi State UniversityAthletic directorZac SelmonHead coachChris Lemonis (6th season)ConferenceSECWest DivisionLocationMississippi State, MississippiHome stadiumDudy Noble Field (Capacity: 15,500)NicknameBulldogsColorsMaroon and white[1] NCAA Tournament champions2021College World Seri…
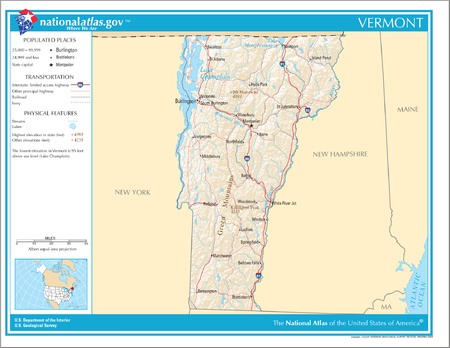
Overview of and topical guide to Vermont See also: Index of Vermont-related articles The Flag of the State of VermontThe Great Seal of the State of Vermont The location of the state of Vermont in the United States of America Vermont The following outline is provided as an overview of and topical guide to the U.S. state of Vermont: Vermont – state in the New England region of the northeastern United States. Vermont is the leading producer of maple syrup in the United States. The state capit…

WWE Hall of Fame induction ceremony WWE Hall of Fame (2009)The WWE Hall of Fame Class of 2009 and their inductorsPromotionWWEDateApril 4, 2009CityHouston, Texas[1]VenueToyota CenterWWE Hall of Fame chronology вҶҗ Previous2008 Next вҶ’2010 WWE Hall of Fame (2009) was the event which featured the introduction of the 10th class to the WWE Hall of Fame. The event was produced by World Wrestling Entertainment (WWE) on April 4, 2009, from the Toyota Center in Houston, Texas. The even…

Disambiguazione вҖ“ West Bank rimanda qui. Se stai cercando il videogioco, vedi Bank Panic. CisgiordaniaCisgiordania - Localizzazione Territorio a status contesoMotivo del contenziosoarea rivendicata interamente dallo Stato di Palestina come proprio territorio Situazione de factoarea sottoposta a controllo misto da parte di Israele e dello Stato di Palestina Posizione dell'ONUriconoscimento di territorio occupato palestinese Dichiarazione d'indipendenza1988 (dichiarata), 1994 (parziale) …

TГјrkiye 1.Lig 1986-1987 Competizione TГјrkiye 1.Lig Sport Calcio Edizione 29ВӘ Organizzatore TFF Luogo Turchia Partecipanti 19 Formula Girone unico Sito web tff.org Risultati Vincitore Galatasaray(7Вә titolo) Retrocessioni Antalyaspor DiyarbakДұrspor Statistiche Miglior marcatore Tanju ГҮolak (25) Incontri disputati 324 Gol segnati 776 (2,4 per incontro) Cronologia della competizione 1985-86 1987-88 Manuale L'edizione 1986-1987 della TГјrkiye 1.Lig vide la vitto…





























