|
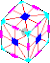
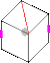
Helicopter Cube The Helicopter Cube is a Rubik's Cube-like puzzle invented by Adam G. Cowan in 2005 and built in 2006.[1][2][3][4][5][6][7] It is also in the shape of a cube. At first glance, the Helicopter Cube may seem like a combination of the 2x2x2 and the Skewb, but it actually cuts differently, and twists around cube edges rather than cube faces. The purpose of the puzzle is to scramble the colors, and then restore them back to their original state of a single color per face. Description The Helicopter Cube is made in the shape of a cube, cut into 8 corner pieces and 24 face center pieces. Each corner piece has 3 colors, and each face center piece has only a single color. Unlike the Rubik's Cube, its faces do not rotate; rather, the pieces are scrambled by rotating around a cube edge. When twisting the puzzle, a 180° turn exchanges two corner pieces and swaps two pairs of face center pieces, but preserves the cube shape. The entire puzzle can be scrambled in this way. However, it is also possible to twist an edge by ~71°, such that the base of two groups of a corner piece and a face center piece each is aligned with the rotational plane of a different edge. The second edge can then be rotated, thus intermixing the corner pieces and the face center pieces and leaving the puzzle in a non-cubical shape. This kind of intermixing is known as a jumbling move. Due to the differing shapes of the intermixed pieces, some rotations possible in the cubical shape may no longer be possible in the jumbled shape. By using a combination of such "jumbling" moves, it is possible to return to cubical shape but with some face center pieces in the wrong orientation, thus jutting outwards like spikes rather than lie flat on the face of the cube. More subtle changes may also be introduced, which are described later. There are four variants of the Helicopter Cube:
Solutions If the puzzle is only scrambled using 180° twists, then it is solvable using only 180° twists. However, if some jumbling moves were made, even if the puzzle was subsequently returned to cube shape, it may not be possible to solve it using only 180° twists. The reason for this is that using only 180° twists, each face center piece can only be permuted within a 6-member cycle, often referred to as its orbit.[6] Face center pieces in different orbits cannot be interchanged using only 180° twists. However, jumbling moves are able to permute face center pieces between different orbits, thus leaving the puzzle in a state that cannot be solved by 180° twists alone. Number of combinationsAssume that Helicopter Cube is scrambled without jumbling moves (i.e. mixed with only 180 degree twists). Any permutation of the corners is possible, including odd permutations. Seven of the corners can be independently rotated, and the orientation of the eighth depends on the other seven, giving 8!×37 combinations. There are 24 face centers, which can be arranged in 24! different ways. But the face centers actually occur in 4 distinct orbits, each containing all colours. So the number of permutations is reduced to 6!4 arrangements.[8] The permutation of the face centers is even, the number of permutations is divided by 2. Assuming the cube does not have a fixed orientation in space, and that the permutations resulting from rotating the cube without twisting it are considered identical, the number of permutations is reduced by a factor of 24. This is because all 24 possible positions and orientations of the first corner are equivalent because of the lack of fixed centres. This factor does not appear when calculating the permutations of N×N×N cubes where N is odd, since those puzzles have fixed centres which identify the cube's spatial orientation. This gives a total number of permutations of The expanded number is 493694233804800000 (approximately 494 billiard on the long scale or 494 quadrillion on the short scale).[6] When a Helicopter Cube is scrambled with jumbling moves but still retains its cube shape, then face centers do not occur in 4 distinct orbits. Assuming that the four centres of each colour are indistinguishable, the number of permutations is reduced to 24!/(4!6) arrangements. The reducing factor comes about because there are 24 (4!) ways to arrange the four pieces of a given colour. This is raised to the sixth power because there are six colours. This gives a total number of permutations of The expanded number is 11928787020628077600000 (approximately 11929 trillion or 12 trilliard on the long scale or 12 sextillion on the short scale)[8] To count non-cube positions, we need to count all the possible shapes (ignoring the colours). Counting those shapes is tricky, since sometimes moves are blocked purely due to the shape of the pieces rather than the underlying mechanism. Matt Galla has done a full analysis, and wrote up his results in this post on TwistyPuzzles Forum. I have reproduced and verified his results. He found 14,098 shapes, or 28,055 if mirror images are counted too. Some of these have symmetry however, and therefore occur in fewer than 24 (or 48) possible orientations. Here is a breakdown of those symmetries:[8]
The row marked Order shows the sizes of the symmetry groups. The Index is the index of the symmetry group as a subgroup of the full cubic symmetry group, i.e. it is 48 divided by the order. The index is also the number of ways any particular shape with that symmetry can be oriented in space (including reflections). The first Shapes row lists the number of shapes that Matt found for each symmetry group but not counting mirror images, and the second Shapes row includes the mirror image shapes in its count. The row marked Total is the product of the index and the number of shapes.[8] Multiplying this with the previous result gives 15568653590593384802320800000 (approximately 15569 quadrillion or 15 quadrilliard on the long scale or 15 octillion on the short scale) jumbled positions altogether.[8] See also
References
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia