|
Friendship graph
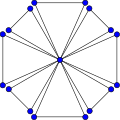
 In the mathematical field of graph theory, the friendship graph (or Dutch windmill graph or n-fan) Fn is a planar, undirected graph with 2n + 1 vertices and 3n edges.[1] The friendship graph Fn can be constructed by joining n copies of the cycle graph C3 with a common vertex, which becomes a universal vertex for the graph.[2] By construction, the friendship graph Fn is isomorphic to the windmill graph Wd(3, n). It is unit distance with girth 3, diameter 2 and radius 1. The graph F2 is isomorphic to the butterfly graph. Friendship graphs are generalized by the triangular cactus graphs. Friendship theoremThe friendship theorem of Paul Erdős, Alfréd Rényi, and Vera T. Sós (1966)[3] states that the finite graphs with the property that every two vertices have exactly one neighbor in common are exactly the friendship graphs. Informally, if a group of people has the property that every pair of people has exactly one friend in common, then there must be one person who is a friend to all the others. However, for infinite graphs, there can be many different graphs with the same cardinality that have this property.[4] A combinatorial proof of the friendship theorem was given by Mertzios and Unger.[5] Another proof was given by Craig Huneke.[6] A formalised proof in Metamath was reported by Alexander van der Vekens in October 2018 on the Metamath mailing list.[7] Labeling and colouringThe friendship graph has chromatic number 3 and chromatic index 2n. Its chromatic polynomial can be deduced from the chromatic polynomial of the cycle graph C3 and is equal to
The friendship graph Fn is edge-graceful if and only if n is odd. It is graceful if and only if n ≡ 0 (mod 4) or n ≡ 1 (mod 4).[8][9] Every friendship graph is factor-critical. Extremal graph theoryAccording to extremal graph theory, every graph with sufficiently many edges (relative to its number of vertices) must contain a -fan as a subgraph. More specifically, this is true for an -vertex graph (for sufficiently large in terms of ) if the number of edges is where is if is odd, and is if is even. These bounds generalize Turán's theorem on the number of edges in a triangle-free graph, and they are the best possible bounds for this problem (when ), in that for any smaller number of edges there exist graphs that do not contain a -fan.[10] GeneralizationsAny two vertices having exactly one neighbor in common is equivalent to any two vertices being connected by exactly one path of length two. This has been generalized to -graphs, in which any two vertices are connected by a unique path of length . For no such graphs are known, and the claim of their non-existence is Kotzig's conjecture. See also
References
|
||||||||||||||||||||||||
Portal di Ensiklopedia Dunia