3-4-6-12 tiling

3-4-6-12 tiling
Type	2-uniform tiling
Vertex configuration	3.4.6.4 and 4.6.12
Symmetry	p6m, [6,3], (*632)
Rotation symmetry	p6, [6,3]^+, (632)
Properties	2-uniform, 4-isohedral, 4-isotoxal

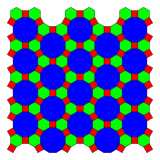
In geometry of the Euclidean plane, the 3-4-6-12 tiling is one of 20 2-uniform tilings of the Euclidean plane by regular polygons, containing regular triangles, squares, hexagons and dodecagons, arranged in two vertex configuration: 3.4.6.4 and 4.6.12.[1][2][3][4]

It has hexagonal symmetry, p6m, [6,3], (*632). It is also called a demiregular tiling by some authors.

Geometry

Its two vertex configurations are shared with two 1-uniform tilings:

rhombitrihexagonal tiling	truncated trihexagonal tiling
3.4.6.4	4.6.12

It can be seen as a type of diminished rhombitrihexagonal tiling, with dodecagons replacing periodic sets of hexagons and surrounding squares and triangles. This is similar to the Johnson solid, a diminished rhombicosidodecahedron, which is a rhombicosidodecahedron with faces removed, leading to new decagonal faces. The dual of this variant is shown to the right (deltoidal hexagonal insets).

Related k-uniform tilings of regular polygons

The hexagons can be dissected into 6 triangles, and the dodecagons can be dissected into triangles, hexagons and squares.

Dissected polygons

Hexagon	Dodecagon (each has 2 orientations)
Dual Processes (Dual 'Insets')

3-uniform tilings
48	26	18 (2-uniform)
[3^6; 3^2.4.3.4; 3^2.4.12]	[3.4^2.6; (3.4.6.4)^2]	[3^6; 3^2.4.3.4]
V[3^6; 3^2.4.3.4; 3^2.4.12]	V[3.4^2.6; (3.4.6.4)^2]	V[3^6; 3^2.4.3.4]
3-uniform duals

Circle Packing

This 2-uniform tiling can be used as a circle packing. Cyan circles are in contact with 3 other circles (2 cyan, 1 pink), corresponding to the V4.6.12 planigon, and pink circles are in contact with 4 other circles (1 cyan, 2 pink), corresponding to the V3.4.6.4 planigon. It is homeomorphic to the ambo operation on the tiling, with the cyan and pink gap polygons corresponding to the cyan and pink circles (mini-vertex configuration polygons; one dimensional duals to the respective planigons). Both images coincide.

C[3.4.6.12]	a[3.4.6.12]

Dual tiling

The dual tiling has right triangle and kite faces, defined by face configurations: V3.4.6.4 and V4.6.12, and can be seen combining the deltoidal trihexagonal tiling and kisrhombille tilings.

Dual tiling

V3.4.6.4 V4.6.12

Deltoidal trihexagonal tiling

Kisrhombille tiling

Notes

1. Critchlow, pp. 62–67
2. Grünbaum and Shephard 1986, pp. 65–67
3. In Search of Demiregular Tilings #4
4. Chavey (1989)

References

• Keith Critchlow, Order in Space: A design source book, 1970, pp. 62–67
• Ghyka, M. The Geometry of Art and Life, (1946), 2nd edition, New York: Dover, 1977. Demiregular tiling #15
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. pp. 35–43
• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman. ISBN 0-7167-1193-1. p. 65
• Sacred Geometry Design Sourcebook: Universal Dimensional Patterns, Bruce Rawles, 1997. pp. 36–37 [1]

External links

• Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
• Dutch, Steve. "Uniform Tilings". Archived from the original on 2006-09-09. Retrieved 2006-09-09.
• Weisstein, Eric W. "Demiregular tessellation". MathWorld.
• In Search of Demiregular Tilings, Helmer Aslaksen
• n-uniform tilings Brian Galebach, 2-Uniform Tiling 1 of 20