|
Integració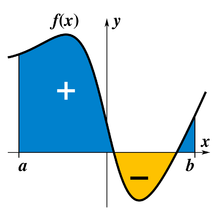 El concepte d'integració és un concepte fonamental de les matemàtiques avançades, especialment en els camps del càlcul i de l'anàlisi matemàtica. Bàsicament, una integral és una generalització de la suma d'infinits sumatoris, infinitament petits. Una integral assigna números a funcions d'una manera que pot descriure el desplaçament, l'àrea, el volum i altres conceptes que sorgeixen combinant dades infinitesimals. La integració és una de les dues principals operacions de càlcul, amb la seva inversa, derivació, que és l'altra. Donada una funció f(x) d'una variable real x i un interval [a,b] de la recta real, la integral és igual a l'àrea de la regió del pla xy limitada entre la gràfica de f, l'eix x, i les línies verticals x = a i x = b, on es resten les àrees que estan per sota de l'eix x. La paraula "integral" també es pot referir a la noció de funció primitiva, és a dir, una funció F, la derivada de la qual és la funció donada f. En aquest cas s'anomena integral indefinida, mentre que les integrals tractades en aquest article són les integrals definides. Alguns autors conserven una distinció entre primitives i integrals indefinides. Els principis de la integració varen ser formulats per Newton i Leibniz a finals del segle xvii. A través del teorema fonamental del càlcul, que varen desenvolupar tots dos de forma independent, la integració es connecta amb la derivació, i la integral definida d'una funció es pot calcular fàcilment un cop se'n coneix una primitiva. Les integrals i les derivades esdevenen eines bàsiques del càlcul, amb nombroses aplicacions en ciència i enginyeria. A començaments del segle xix, Bernhard Riemann va donar una definició rigorosa de la integral. Es basa en un límit que aproxima l'àrea d'una regió curvilínia a base de partir-la en petits bocins verticals. Posteriorment varen començar a aparèixer nocions més sofisticades de la integral, on s'han generalitzat els tipus de les funcions i els dominis sobre els quals es fa la integració. La integral curvilínia es defineix per funcions de dues o tres variables, i l'interval d'integració [a,b] se substitueix per una certa corba que connecta dos punts del pla o de l'espai. En una integral de superfície, la corba se substitueix per un bocí d'una superfície a l'espai de tres dimensions. Els conceptes moderns d'integració es basen en la teoria matemàtica abstracta coneguda com a teoria de la mesura, que va desenvolupar Henri Lebesgue a principis del segle xx. Les integrals de les formes diferencials juguen un rol fonamental en la geometria diferencial moderna. Aquestes generalitzacions de la integral varen sorgir primer a partir de les necessitats de la física, i tenen un paper important en la formulació de moltes lleis físiques com, per exemple, les de l'electromagnetisme. HistòriaIntegració abans del càlculLa integració es pot resseguir en el passat fins a l'antic Egipte, circa 1800 aC, amb el Papir de Moscou, on es demostra que ja es coneixia una fórmula per calcular el volum d'un tronc piramidal.[1][2] La primera tècnica sistemàtica documentada capaç de determinar integrals és el mètode d'exhaustió d'Èudox (c. 370 aC), que mirava de trobar àrees i volums a base de partir-los en un nombre infinit de formes per les quals l'àrea o el volum fossin coneguts. Aquest mètode va ser desenvolupat i usat més endavant per Arquimedes, que el va emprar per calcular àrees de paràboles i una aproximació a l'àrea d'un cercle. Mètodes similars varen ser desenvolupats de forma independent a la Xina al voltant del segle iii per Liu Hui, que els va fer servir per trobar l'àrea del cercle. Més tard, Zu Chongzhi va fer servir aquest mètode per trobar el volum d'una esfera.[2] Algunes idees de càlcul integral es troben al Siddhanta Shiromani, un llibre d'astronomia del segle xii del matemàtic indi Bhaskara II. Fins al segle xvi no varen començar a aparèixer avenços significatius sobre el mètode d'exhaustió. En aquesta època, d'una banda, el treball de Cavalieri amb el seu mètode dels indivisibles i, de l'altra, els treballs de Fermat, varen començar a desenvolupar els fonaments del càlcul modern. A inicis del segle xvii, es varen produir nous avenços amb les aportacions de Barrow i Torricelli, que varen presentar els primers indicis d'una connexió entre la integració i la derivació. Newton i LeibnizEls principals avenços en integració varen venir al segle xvii amb el descobriment del teorema fonamental del càlcul, realitzat de manera independent per Newton i Leibniz. El teorema demostra una connexió entre la integració i la derivació. Aquesta connexió, combinada amb la facilitat (comparativament parlant) del càlcul de derivades, es pot fer servir per calcular integrals. En particular, el teorema fonamental del càlcul permet resoldre una classe més ampla de problemes. També cal destacar tot el marc estructural al voltant de les matemàtiques que varen desenvolupar també tots dos, Newton i Leibniz; l'anomenat càlcul infinitesimal va permetre d'analitzar, de forma precisa, funcions amb dominis continus. Posteriorment, aquest marc ha esdevingut el càlcul modern, i la notació per les integrals procedeix directament del treball de Leibniz. Formalització de les integralsEncara que Newton i Leibniz varen subministrar un enfocament sistemàtic a la integració, el seu treball està mancat d'un cert nivell de rigor. És memorable l'atac del bisbe Berkeley qualificant els infinitesimals com "els fantasmes de les quantitats que s'esvaeixen". El càlcul va adquirir una posició més ferma amb el desenvolupament dels límits i, a la primera meitat del segle xix, va rebre una fonamentació adequada per part de Cauchy. La integració va ser rigorosament formalitzada per primera vegada per Riemann, emprant límits. Malgrat que totes les funcions contínues fragmentades i fitades són integrables segons la definició de Riemann en un interval fitat, més tard, es varen considerar funcions més generals per les quals no s'aplica la definició de Riemann. A principis del segle xx, Lebesgue va formular una definició diferent de la integral, basada en la teoria de la mesura, que és aplicable a moltes més funcions i conserva els mateixos resultats per les integrals que es poden calcular segons la definició de Riemann. També es varen proposar altres definicions d'integral, que amplien les definicions de Riemann i Lebesgue. NotacióIsaac Newton, per indicar integració feia servir una petita barra vertical damunt d'una variable, o posava la variable dins d'una caixa. La barra vertical es confonia fàcilment amb o , que Newton feia servir per indicar la derivació, i la notació "caixa" era difícil de reproduir pels impressors; per això, aquestes notacions no varen ser adoptades àmpliament. La notació moderna de les integrals indefinides va ser presentada per Gottfried Leibniz el 1675.[3][4] Per indicar summa (en llatí, "suma" o "total"), va adaptar el símbol integral, "∫", estirant una S llarga. La notació moderna de la integral definida, amb els límits a dalt i a baix del signe integral, la va fer servir per primer cop Joseph Fourier a Mémoires de l'Acadèmia Francesa, que va escriure al voltant de 1819–20 i que es va reimprimir en el seu llibre de 1822.[5][6]
En la notació matemàtica en àrab modern, que s'escriu de dreta a esquerra, es fa servir un signe integral invertit Terminologia i notacióSi una funció té una integral, es diu que és integrable. De la funció de la qual es calcula la integral es diu que és l'integrand. De la regió sobre el qual s'integra la funció se'n diu el domini d'integració. Si la integral no té un domini d'integració, es considera indefinida (la que té domini es considera definida). En general, l'integrand pot ser una funció de més d'una variable, i el domini d'integració pot ser una àrea, un volum, una regió de dimensió superior, o fins i tot un espai abstracte que no té estructura geomètrica en cap sentit usual. El cas més senzill, la integral d'una funció real f d'una variable real x sobre l'interval [a, b], s'escriu El signe ∫ és una "S" allargada que representa integració; a i b són respectivament el límit inferior i el límit superior de la integració i defineixen el domini d'integració; f és l'integrand, que s'ha d'avaluar en variar x sobre l'interval [a,b]; i dx pot tenir diferents interpretacions depenent de la teoria que es faci servir. Per exemple, pot ser vist simplement com la indicació que x és la variable d'integració, com una representació dels pesos en la suma de Riemann, com una mesura (en la integració de Lebesgue i les seves extensions), com un infinitesimal (en anàlisi no estàndard) o com una quantitat matemàtica independent: una forma diferencial. Casos més complicats poden variar la notació lleugerament. Concepte d'integralLes integrals apareixen en moltes situacions pràctiques. Considereu una piscina. Si és rectangular, llavors, a partir de les seves longitud, amplada i alçada, es pot determinar fàcilment el volum d'aigua que pot contenir (per omplir-la), l'àrea de la superfície (per cobrir-la), i la llargada de la seva vora (per lligar-la). Tanmateix, si és oval amb un fons arrodonit, totes aquestes quantitats demanen integrals. En alguns casos pot ser suficient amb aproximacions pràctiques, però en la majoria de casos caldran respostes exactes i rigoroses a aquesta mena de problemes. Posem un exemple: 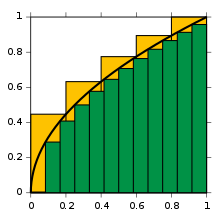 Per començar, es considerarà la corba y = f(x) entre x = 0 i x = 1, amb f(x) = √x. La pregunta és:
D'aquesta àrea (encara desconeguda) se'n dirà la integral de f. La notació per aquesta integral serà
Com a primera aproximació, es mira al quadrat unitat donat pels costats x=0 fins a x=1 i y=f(0)=0 i y=f(1)=1. La seva àrea és exactament 1. Tal com es pot veure el verdader valor de la integral ha de ser d'alguna forma més petit. Reduint l'amplada dels rectangles emprats per fer l'aproximació s'obtindrà un millor resultat; així, es parteix l'interval en cinc passos, emprant per a l'aproximació els punts 0, ¹⁄₅, ²⁄₅, així fins a 1. S'ajusta una caixa cada pas emprant l'alçada del cantó dret de cada bocí de la corba, així √¹⁄₅, √²⁄₅, i així fins a √1 = 1. Sumant les àrees d'aquests rectangles, s'obté una aproximació millor de la integral que s'està buscant, Fixeu-vos que s'està sumant una quantitat finita de valors de la funció f, multiplicats per la diferència entre dos punts d'aproximació successius. Es pot veure fàcilment que l'aproximació continua donant un valor més gran que el de la integral. Emprant més passos s'obté una aproximació més ajustada, però no serà mai exacta: si en comptes de 5 subintervals se'n prenen dotze i s'agafa el valor de l'esquerra, tal com es mostra al dibuix, s'obté un valor aproximat per l'àrea, de 0.6203, que en aquest cas és massa petit. La idea clau és la transició des de la suma d'una quantitat finita de diferències de punts d'aproximació multiplicats pels respectius valors de la funció, cap a fer servir passos infinitament fins, o infinitesimals. La notació concep la integral com una suma ponderada (denotada per la "S" allargada), dels valors de la funció (com les alçades, y = f(x)) multiplicats per passos d'amplada infinitesimal, els anomenats diferencials (indicats per dx). Pel que fa al càlcul d'integrals, el teorema fonamental del càlcul, degut a Newton i Leibniz, és el lligam fonamental entre les operacions de derivació i integració. Sota condicions adequades, el valor d'una integral sobre una regió, es pot determinar a base de mirar només a la frontera de la regió. Aplicat això a la corba arrel quadrada, s'ha de mirar la funció relacionada , i simplement agafar F(1)−F(0), on 0 i 1 són les fronteres de l'interval [0,1]. (Aquest és un exemple d'una regla general, que diu que per f(x) = xq, amb q ≠ −1, la funció relacionada, l'anomenada primitiva és F(x) = (xq+1)/(q+1).) Històricament, després que els primers esforços de definir rigorosament els infinitesimals no fructifiquessin, Riemann va definir formalment les integrals com el límit de sumes ponderades, de forma que el dx suggereix el límit d'una diferència (l'amplada de l'interval). Els efectes de la dependència de la definició de Riemann en els intervals i la continuïtat varen motivar noves definicions, especialment la integral de Lebesgue, que es basa en l'habilitat d'estendre la idea de "mesura" de formes molt més flexibles. Així la notació Es refereix a una suma ponderada del valors en què es divideix la funció, on μ mesura el pes que s'ha d'assignar a cada valor. (Aquí A indica la regió d'integració.) La geometria diferencial, amb el seu "càlcul de varietats", encara dona una altra interpretació a aquesta notació familiar. Ara f(x) i dx esdevenen una forma diferencial, ω = f(x)dx, apareix un nou operador diferencial d, conegut com la derivada exterior, i el teorema fonamental esdevé el (més general) teorema de Stokes, a partir del qual se'n segueixen el teorema de Green, el teorema de la divergència, i el teorema fonamental del càlcul. Recentment, els infinitesimals han reaparegut amb rigor, a través d'innovacions modernes com l'anàlisi no estàndard. Aquests mètodes no només reivindiquen la intuïció dels pioners, també porten cap a noves matemàtiques, i fan més intuïtiu i comprensible el treball amb càlcul infinitesimal. Tot i que hi ha diferències entre totes aquestes concepcions de la integral, hi ha una superposició considerable. Així, l'àrea de la piscina oval es pot trobar com una el·lipse geomètrica, com una suma d'infinitesimals, com una integral de Riemann, com una integral de Lebesgue, o com una varietat amb una forma diferencial. El resultat obtingut amb el càlcul serà el mateix en tots els casos. Definicions formalsHi ha moltes formes de definir formalment una integral, no totes són equivalents. Les diferències existeixen principalment per tractar casos especials que poden no ser integrables amb les altres definicions, però ocasionalment també per motius pedagògics. Les definicions d'integral que es fan servir més habitualment són les integrals de Riemann i les integrals de Lebesgue. Integral de Riemann La integral de Riemann es defineix en termes de sumatoris de Riemann de funcions respecte de particions etiquetades d'un interval. Sia [a,b] un interval tancat de la recta real; llavors una partició etiquetada de [a,b] és una seqüència finita:  Això divideix l'interval [a,b] en i subintervals [xi−1, xi], cada un dels quals és "etiquetat" amb un punt específicat ti de; [xi−1, xi]. Sia Δi = xi−xi−1 l'amplada del subinterval i; el pas d'aquesta partició etiquetada és l'amplada del subinterval més gran obtingut per la partició, maxi=1…n Δi. Un sumatori de Riemann d'una funció f respecte d'aquesta partició etiquetada es defineix com Així cada terme del sumatori és l'àrea del rectangle amb alçada igual al valor de la funció en el punt especificat del subinterval donat, i de la mateixa amplada que l'amplada del subinterval. La integral de Riemann d'una funció f sobre l'interval [a,b] és igual a S si:
Quan les etiquetes escollides donen el màxim (o mínim) valor de la funció en el respectiu integral, el sumatori de Riemann esdevé un sumatori de Darboux superior (o inferior), això suggereix l'estreta connexió que hi ha entre la integral de Riemann i la integral de Darboux. Integral de LebesgueLa integral de Riemann no està definida per un ample ventall de funcions i situacions d'importància pràctica (i d'interès teòric). Per exemple, la integral de Riemann pot integrar fàcilment la densitat per tal d'obtenir la massa d'una biga d'acer, però no es pot adaptar a una bola d'acer que s'hi recolza al damunt. Això motiva la creació d'altres definicions, sota les quals es pot integrar un assortit més ample de funcions.[8] La integral de Lebesgue, en particular, assoleix una gran flexibilitat a base de centrar l'atenció en els pesos de la suma ponderada. Així, la definició de la integral de Lebesgue comença amb una mesura, μ. En el cas més senzill, la mesura de Lebesgue μ(A) d'un interval A = [a,b] és la seva amplada, b − a, així la integral de Lebesgue coincideix amb la integral de Riemann quan les dues existeixen. En casos més complicats, els conjunts a mesurar poden estar altament fragmentats, sense continuïtat ni semblança a intervals. Per explotar aquesta flexibilitat, la integral de Lebesgue inverteix l'enfocament de la suma ponderada. Com ho expressa Folland:[9] "Per calcular la integral de Riemann de f, es parteix el domini [a,b] en subintervals", mentre que en la integral de Lebesgue, "de fet el que s'està partint és el recorregut de f". Un enfocament habitual, primer defineix la integral de la funció característica d'un conjunt mesurable A per:
Això s'estén per linealitat a les funcions esglaonades simples, que només tenen un nombre finit n, de valors diferents no negatius: (on la imatge de Ai en aplicar-li la funció esglaonada s és el valor constant ai). Així si E és un conjunt mesurable, es defineix Llavors, per qualsevol funció mesurable no negativa f es defineix És a dir, s'estableix que la integral de f és el suprem de totes les integrals de funcions esglaonades que són més petites o iguals que f. Una funció mesurable qualsevol f, se separa entre els seus valors positius i negatius a base de definir Finalment, f és Lebesgue integrable si I llavors es defineix la integral per Quan l'espai mètric en el que estan definides les funcions és també un espai topològic localment compacte (com és el cas dels nombres reals ℝ), les mesures compatibles amb la topologia en un sentit adequat (mesura de Radon, de les quals la mesura de Lebesgue n'és un exemple) una integral respecte d'elles es pot definir d'un altra manera, es comença a partir de les integrals de les funcions contínues amb suport compacte. De forma més precisa, les funcions compactament suportades formen un espai vectorial que comporta una topologia natural, i es pot definir una mesura (Radon) com a qualsevol funcional lineal continu d'aquest espai; llavors el valor d'una mesura a una funció compactament suportada, és també, per definició, la integral de la funció. Llavors es continua expandint la mesura (la integral) a funcions més generals per continuïtat, i es defineix la mesura d'un conjunt com la integral de la seva funció característica. Aquest és l'enfocament que pren Bourbaki[10] i cert nombre d'altres autors. Per més detalls, vegeu mesures de Radon. Altres definicions d'integralTot i que les integrals de Riemann i Lebesgue són les definicions més importants d'integral, n'hi ha unes quantes més, incloent-hi:
Propietats de la integracióLinealitat
La linealitat, conjuntament amb algunes propietat naturals de continuïtat i la normalització per certes classes de funcions "simples", es poden fer servir per donar una definició alternativa d'integral. Aquest és l'enfocament de Daniell pel cas de funcions reals en un conjunt X, generalitzat per Bourbaki a funcions que prenen valors en un espai vectorial topològicament compacte. Vegeu Hildebrandt (1953)[11] per una caracterització axiomàtica de la integral. Desigualtats amb integralsEs verifiquen diverses desigualtats generals per funcions Riemann integrables definides en un interval tancat i fitat [a, b] i es poden generalitzar a altres nocions d'integral (Lebesgue i Daniell).
Propietats relatives als límits d'integracióEn aquesta secció f és una funció real Riemann integrable. La integral sobre un interval [a, b] està definida si a ≤ b. Això significa que els sumatoris superiors i inferiors de la funció f s'avaluen sobre una partició a = x0 ≤ x1 ≤. .. ≤ xn = b els valors de la qual xi són creixents. Geomètricament això significa que la integració té lloc "d'esquerra a dreta", avaluant f dins d'intervals [x i , x i +1] on l'interval amb un índex més gran queda a la dreta de l'interval amb un índex més petit. Dels valors a i b, els punts extrems del interval, se'n diu els límits d'integració de f. Les integrals també es poden definir si a > b:
Això, amb a = b, implica:
La primera convenció és necessària al calcular integrals sobre subintervals de [a, b]; la segona diu que una integral sobre un interval degenerat, o un punt, ha de ser zero. Un motiu per la primera convenció és que la integrabilitat de f sobre un interval [a, b] implica que f és integrable sobre qualsevol subinterval [c, d], però en particular, les integrals tenen la propietat que:
Amb la primera convenció la relació resultant queda ben definida per qualsevol permutació cíclica de a, b, i c. En comptes de veure l'anterior com a convencions, també es pot adoptar el punt de vista que la integració es fa només sobre varietats orientades. Si M és una tal forma m-dimensional orientada, i M' és la mateixa forma amb orientació oposada i ω és una m-forma, llavors es té (vegeu més avall per integració de formes diferencials): Teorema fonamental del càlculEl teorema fonamental del càlcul és l'afirmació que la derivació i la integració són operacions inverses: si una funció contínua primer s'integra i llavors es deriva, es recupera la funció original. Una conseqüència important, de vegades anomenada el segon teorema fonamental del càlcul, permet de calcular integrals a base d'emprar una primitiva de la funció a integrar. Enunciat dels teoremes
Càlcul d'integralsPer calcular una integral es pot buscar una primitiva de la funció i llavors aplicar el teorema fonamental del càlcul per determinar el valor de la integral. Aquesta tècnica es pot intentar automatitzar mitjançant programes d'ordinador que implementin algorismes d'integració simbòlica. No sempre és possible trobar la primitiva d'una funció i de vegades, tot i que és possible, el resultat és molt complex. Una altra forma de trobar un valor aproximat de la integral és emprant el que s'anomena quadratura numèrica, que és un conjunt d'algorismes que permeten calcular de forma aproximada el valor de la integral directament sense trobar primer la funció primitiva. A partir del càlcul de primitivesLa tècnica més bàsica per calcular integrals d'una variable real es basa en el teorema fonamental del càlcul. Es procedeix de la següent forma:
Fixeu-vos que la integral no és exactament la primitiva, sinó que el teorema fonamental permet emprar les primitives per avaluar les integrals definides. El pas difícil d'aquest procés és sovint el de trobar una primitiva de f. Rarament és possible donar un cop d'ull a una funció i escriure directament la seva primitiva. Molt sovint, és necessari emprar una de les moltes tècniques que s'han desenvolupat per calcular integrals. La majoria d'aquestes tècniques transformen una integral en una altra que s'espera que sigui més tractable. Aquestes tècniques inclouen:
Fins i tot si aquestes tècniques fallen, encara és possible d'avaluar una integral donada. La següent tècnica més comuna és el càlcul de residus, mentre que la sèrie de Taylor es pot fer servir de vegades per trobar la primitiva de les integrals no elementals; és el que es coneix com el mètode d'integració per sèries. També hi ha moltes formes menys habituals per calcular integrals definides; per exemple la identitat de Parseval es pot fer servir per transformar una integral sobre una regió rectangular en una suma infinita. En algunes ocasions, una integral es pot avaluar emprant un truc; un exemple d'aquest tipus es pot veure a la integral de Gauß. Els càlcul de volums de sòlids de revolució normalment es pot fer amb la integració per discs o la integració per capes. Els resultats específics que s'han trobat emprant les diferents tècniques es recullen a la taula d'integrals. Algorismes simbòlics de càlcul de primitivesMolts problemes de matemàtiques, física, i enginyeria impliquen integració on es desitja una fórmula explícita per la integral. Amb aquesta finalitat, al llarg dels anys s'han publicat extenses taules d'integrals. Amb l'expansió dels ordinadors, molts professionals, educadors, i estudiants s'han fixat en els sistemes de càlcul algebraic per ordinador que han estat dissenyats específicament per desenvolupar tasques tedioses o difícils, incloent integració. La integració simbòlica presenta un repte especial en el desenvolupament d'aquest tipus de sistemes. Una dificultat matemàtica important de la integració simbòlica és que, en molts casos, una fórmula tancada per la primitiva d'una funció aparentment innocent, simplement no existeix. Per exemple, se sap que les primitives de les funcions exp (x²), xx i sin (x)/x no es poden expressar amb una fórmula tancada que impliqui només fraccions racionals, exponencials funcions, logarítmiques, funcions trigonomètriques, inverses de les funcions trigonomètriques, i les operacions de suma, multiplicació i composició; en altres paraules, cap d'aquestes tres funcions donades és integrable amb funcions elementals. La teoria diferencial de Galois dona els criteris generals per determinar quan la primitiva d'una funció elemental és elemental. Desgraciadament, resulta que les funcions amb expressions tancades per les seves primitives són l'excepció en comptes de la regla. En conseqüència, els sistemes de càlcul algebraic per ordinador no poden tenir cap esperança de poder trobar una primitiva per una funció elemental qualsevol construïda de forma aleatòria. Al cantó positiu, si els blocs constructius de les primitives són fixats d'antuvi, encara és possible de decidir si la primitiva d'una funció donada es pot expressar emprant aquests blocs i les operacions de multiplicació i composició, i de trobar la resposta simbòlica en el cas que existeixi. L'algorisme de Risch, implementat a Mathematica i al Maple, fa precisament això per funcions i primitives construïdes a partir de fraccions racionals, radicals, logaritmes i funcions exponencials. Alguns integrands especials apareixen amb prou freqüència per garantir-ne un estudi especial. En particular, pot ser útil de tenir, en el conjunt de primitives, les funcions especials de la física (com les funcions de Legendre, la funció hipergeomètrica, la funció Gamma i així). Estendre l'algorisme de Risch-Norman de forma que inclogui aquestes funcions és possible però és tot un repte. La majoria de les persones no són capaces d'integrar aquestes fórmules generals, així, en cert sentit, els ordinadors són més hàbils integrant fórmules altament complicades. És poc probable que les fórmules molt complexes tinguin primitives de forma tancada, per tant fins a quin punt això és un avantatge és una qüestió filosòfica oberta al debat. Per quadratura numèricaLes integrals que es troben en els cursos bàsics de càlcul han estat triades deliberadament per la seva simplicitat; les que es troben en aplicacions reals no sempre són tan avinents. Algunes integrals no es poden trobar exactament, algunes necessiten funcions especials que elles mateixes són tot un repte per calcular-les, i d'altres són tan complexes que trobar la resposta exacta és massa lent. Això motiva l'estudi i l'aplicació de mètodes numèrics per aproximar integrals, els quals, avui en dia fan servir aritmètica de coma flotant en ordinadors. Moltes de les idees varen sorgir molt abans, per les calculadores manuals; però la velocitat dels ordinadors de propòsit general han creat la necessitat de millores. Els objectius de la integració numèrica són exactitud, fiabilitat, eficiència i generalitat. Els mètodes sofisticats poden millorar molt un mètode ingenu en totes quatre mesures (Dahlquist i Björck,;[12] Kahaner, Moler i Nash;[13] Stoer i Bulirsch[14]). Per exemple, la integral que té la resposta exacta de 94⁄25 = 3.76. (en la pràctica ordinària, la resposta no és coneguda per endavant, per tant una tasca important — que no s'explora aquí — és decidir en quin moment una aproximació ja és prou bona.) Un enfocament de "llibre de càlcul" divideix l'interval d'integració en, per exemple, 16 bocins iguals, i calcula els valors de la funció.
 Emprant el cantó esquerra de cada bocí, el mètode rectangular suma 16 valors de la funció i multiplica per l'amplada del pas, h, en aquest cas 0.25, i obté una valor aproximat de 3.94325 per la integral. L'exactitud no és impressionant, però formalment el càlcul empra bocins d'amplada infinitesimal, per tant d'entrada això no sembla que hagi de ser motiu de preocupació. Efectivament, doblant repetidament el nombre de passos s'arriba a obtenir una aproximació de 3.76001. Ara bé, han fet falta 218 bocins, un cost computacional gran per una exactitud tan petita; i buscar precisions més grans pot forçar a fer passos tan petits que la precisió aritmètica esdevé un obstacle. Una aproximació millor substitueix les parts superiors dels rectangles per segments inclinats que toquen la funció als extrems de cada bocí. Aquest mètode trapezial és gairebé igual de fàcil de calcular; suma els 17 valors de la funció, però al primer i al últim els dona un pes de la meitat, i altre cop multiplica per l'amplada del pas. Això millora l'aproximació de forma immediata a 3.76925, que és notablement més exacte. És més, només calen 2¹⁰ bocins per assolir una exactitud de 3.76000, substancialment menys potència de càlcul per obtenir una exactitud comparable. El mètode de Romberg construeix el mètode del trapezoide amb un efecte més gran. Primer, la longitud dels passos es parteix de forma incremental, donades les aproximacions trapezoïdals indicades per T(h0), T(h1), i així, on hk+1 és la meitat de hk. Per cada nova mida de pas, només cal calcular la meitat dels valors de la funció; els altres s'agafen de la partició amb la mida prèvia (tal com es mostra a la taula de més amunt). Tanmateix, la idea realment potent és la d'interpolar un polinomi a través de les aproximacions, i extrapolar a T(0). Amb aquest mètode una resposta numèricament exacta només requereix quatre bocins (cins valors de la funció)! El polinomi de Lagrange que interpola {hk,T(hk)}k=0…2 = {(4.00,6.128), (2.00,4.352), (1.00,3.908)} is 3.76+0.148h², produeix el valor extrapolat exacte 3.76 a h = 0. Per obtenir aproximacions millors, amb la quadratura de Gauss normalment fa falta molta menys feina. En aquest exemple, pot calcular els valors de la funció només a dues posicions de x, ±²⁄√3, llavors dobla cada valor i els suma per obtenir la resposta numèrica exacta. L'explicació d'aquest èxit dramàtic recau en l'anàlisi de l'error i en una mica de sort. Un mètode de Gauss de n punts és exacte per polinomis de fins a grau n−1. La funció d'aquest exemple és un polinomi de grau 3, més un terme que s'anul·la perquè els punts finals escollits són simètrics respecte al zero. (L'anul·lació d'aquest terme també beneficia el mètode de Romberg.) Desplaçant l'interval a l'esquerra en deixa una mica, si la integral és des de −2.25 fins a 1.75, s'elimina la simetria. De totes maneres, el mètode trapezoïdal és més aviat lent, el mètode d'interpolació polinòmica de Romberg és acceptable — Si el nombre de punts és conegut per endavant. La interpolació racional, també pot fer servir les mateixes avaluacions trapezoïdals del mètode de Romberg per tal d'obtenir un efecte més gran.
A la pràctica, cada mètode ha d'utilitzar avaluacions extra per tal d'assegurar una fita del error en una funció desconeguda; això tendeix a eliminar alguns avantatges del mètode de Gauss pur, i motiva el popular mètode híbrid de Gauss–Kronrod. La simetria encara es pot explotar a base de dividir la integral en dos intervals, des de −2.25 fins a −1.75 (no simètric), i des de −1.75 fins a 1.75 (simètric). De forma més ampla, la quadratura adaptativa parteix un interval entre bocins basant-se en les propietats de la funció, així els punts de dades es concentren on són més necessaris. Aquesta introducció breu omet les integrals de dimensió superior (per exemple, càlculs d'àrea i de volum), on alternatives tals com el mètode de integració de Montecarlo tenen gran importància. Un text de càlcul no es pot substituir per l'anàlisi numèrica, però la inversa també és certa. Fins i tot el millor codi numèric adaptatiu, de vegades requereix que l'usuari ajudi amb les integrals que necessiten més potència de càlcul. Per exemple, les integrals impròpies poden requerir un canvi de variable o mètodes que puguin evitar que la funció presenti valors infinits; i propietats conegudes com la simetria i la periodicitat poden subministrar avantatges crítics. AplicacionsValor mitjà d'una funcióPer calcular el valor mitjà m d'una funció f en un interval [a,b] es fa servir la següent fórmula: Fixeu-vos que, si la funció f és una funció esglaonada amb graons d'igual amplada, aquesta definició coincideix amb la mitjana aritmètica dels valors de la funció. Si els graons tenen amplades diferents, llavors coincideix amb la mitjana aritmètica ponderada on el valor de la funció a cada graó es pondera amb l'amplada del graó. Per tant, aquesta definició es pot entendre com l'extensió natural de la mitjana. En fabricació mecànica es fa servir aquesta definició. Si f(x) és la mida d'una superfície física donada per un rugosímetre i aquesta superfície s'ha fabricat pretenent obtenir una superfície plana, llavors el valor m és la cota mitjana de la superfície, per trobar la rugositat mitjana es torna a aplicar la definició sobre la funció g(x)=|f(x)-m|. Aplicacions en físicaMoltes lleis de la física s'expressen en forma d'equacions diferencials en el cas més senzill aquestes equacions diferencials es resolen amb el càlcul d'una primitiva i moltes vegades el resultat final que es busca es troba amb el càlcul d'una integral. Per exemple, la integral s'aplica per resoldre el problema de la caiguda lliure d'un cos sotmès a la gravetat de la terra. A la Terra, l'acceleració de la gravetat és aproximadament g = 9,81 m/s². Per tant, un cos que cau lliurement començant la seva caiguda amb velocitat nul·la té una velocitat que ve donada per la següent funció: El signe negatiu és degut al fet que la gravetat és cap al centre de la terra i els sistemes de referència normalment es trien de forma que la direcció positiva és cap amunt. Si es vol saber la distància que ha recorregut el cos durant un temps donat T es pot raonar (emprant anàlisi no estàndard) que entorn a cada instant t la velocitat és constant tret de variacions infinitesimals, per tant l'espai recorregut en aquest instant durant un període infinitesimal dt és v(t)dt la suma de tots els espais recorreguts durant tots els instants des de t=0 fins a t=T (el moment en què es vol saber la distància recorreguda) es calcula amb la integral:
El resultat d'aquesta integral és:
Altres exemples de camps de la física on s'apliquen les integrals:
ExtensionsIntegrals impròpies té interval no fitats tant al domini com al recorregut. Una integral de Riemann "pròpia" suposa que l'integrand està definit i és finit en un interval tancat i fitat, els extrems del qual són els límits d'integració. Una integral impròpia apareix quant una o més d'aquestes condicions no se satisfà. En alguns casos questes integrals es poden definir prenent el límit d'una successió d'integrals de Riemann pròpies sobre intervals successivament més llargs. Si l'interval no és fitat, per exemple al seu extrem superior, llavors la integral impròpia és el límit quant el punt final tendeix a infinit. Si l'integrand només està definida en un interval finit semiobert, per exemple (a,b], llavors, altre cop el límit pot subministrar un resultat finit. Això és, la integral impròpia és el límit d'integrals pròpies qun un dels punts extrems de l'interval d'integració s'aproxima, ja sigui a un nombre real especificat o a −∞. En casos més complicats, calen límits aIs dos punts extrems o a punts interiors. Per exemple, la funció integrada des de 0 a ∞ (imatge de la dreta). A l'extrem inferior, a mesura que x s'apropa a 0 la funció tendeix a ∞, i l'extrem superior és ell mateix ∞, tot i que la funció tendeix a 0. Així aquesta és una integral doblement impròpia. Integrada, per exemple, des de 1 fins a 3, amb un sumatori de Riemann ordinari n'hi ha prou per obtenir un resultat de . Per integrar des de 1 fins a ∞, un sumatori de Riemann no és possible. Ara bé, qualsevol límit superior finit, per exemple t (amb t > 1), dona un resultat ben definit, . Aquest resultat té un límit finit quan t tendeix a infinit, que és . De forma semblant, la integral des de ¹⁄₃ fins a 1 admet també un sumatori de Riemann, que per casualitat dona altre cop . Substituint ¹⁄₃ per un valor positiu arbitrari s (amb s < 1) resulta igualment un resultat definit i dona . Aquest, també té un límit finit quan s tendeix a zero, que és . Combinant els límits dels dos fragments, el resultat d'aquesta integral impròpia és Aquest procés no té l'èxit garantit; un límit pot no existir, o pot ser infinit. Per exemple, sobre l'interval tancat de 0 a 1 la integral de no convergeix; i sobre l'interval obert de l'1 a ∞ la integral de no convergeix.  no està fitada internament, però tots dos límits (per la dreta i per l'esquerra) existeixen. També pot passar que un integrand no estigui fitat en un punt interior, en aquest cas la integral s'ha de partir en aquest punt, i el límit de les integrals de tots dos cantons han d'existir i han de ser fitats. Així En a la integral similar no se li pot assignar un valor d'aquesta forma, atès que les integrals per damunt i per davall de zero no convergeixen independentment l'una de l'altra. (En canvi, vegeu valor principal de Cauchy.) Integració múltiple Les integrals es poden calcular sobre regions diferents dels intervals. En general, una integral sobre un conjunt E d'una funció f s'escriu: Aquí x no cal que sigui necessàriament un nombre real, sinó que pot ser qualsevol altra quantitat adequada, per exemple, un vector de R3. El teorema de Fubini demostra que aquestes integrals poden ser reescrites com una integral iterada. En altres paraules, la integral es pot calcular a base d'integrar les coordenades una per una. Si la integral definida d'una funció positiva representa l'àrea de la regió tancada entre la gràfica de la funció i l'eix x, la integral doble d'una funció positiva de dues variables representa el volum de la regió compresa entre la superfície definida per la funció i el pla que conté el seu domini.[15] Si el nombre de variables és més gran, llavors la integral representa un hipervolum, el volum d'un sòlid de més de tres dimensions, que no es pot representar gràficament. Per exemple, el volum del paral·lelepípede de cares 4 × 6 × 5 es pot obtenir de dues maneres:
Integrals curvilínies El concepte d'integral es pot estendre a dominis d'integració més generals, tals com les línies corbes i les superfícies. Aquestes integrals es coneixen com integrals curvilínies i integrals de superfície respectivament. Tenen importants aplicacions a física quan es tracta amb camps vectorials. Una integral curvilínia (anomenada de vegades integral de camí) és una integral on la funció a integrar és avaluada al llarg d'una corba. Es fan servir diverses integrals curvilínies diferents. En el cas d'una corba tancada també se'n diu una integral de contorn. La funció a integrar pot ser un camp escalar o un camp vectorial. El valor de la integral curvilínia és la suma dels valors del camp als punts de la línia, ponderats per alguna funció escalar de la corba (habitualment la longitud de l'arc o, pel cas d'un camp vectorial, el producte escalar del camp vectorial per un vector diferencial de la corba). Aquesta ponderació distingeix les integrals curvilínies de les integrals més senzilles definides sobre intervals. Moltes fórmules senzilles de la física tenen de manera natural anàlogues contínues en termes d'integrals curvilínies; per exemple, el fet que el treball sigui igual a la força multiplicada per la distància es pot expressar (en termes de quantitats vectorials) com: Que té el seu paral·lel en integral curvilínia: Que acumula els components vectorials al llarg d'un camí continu, i així troba el treball fet per un objecte en moure's a través d'un camp, com ara un camp elèctric o un camp gravitatori. Integrals de superfície Una integral de superfície és una integral definida calculada sobre una superfície (que pot ser un conjunt corbat a l'espai) es pot entendre com la integral doble anàloga a la integral curvilínia. La funció a integrar pot ser un camp escalar o un camp vectorial. El valor de la integral de superfície és la suma ponderada dels valors del camp a tots els punts de la superfície. Això es pot aconseguir a base de dividir la superfície en elements de superfície, els quals proporcionen la partició pels sumatoris de Riemann. Com a exemple de les aplicacions de les integrals de superfície, es pot considerar un camp vectorial v sobre una superfície S; és a dir, per cada punt x de S, v(x) és un vector. Imagineu que es té un fluid fluint a través de S, de forma que v(x) determina la velocitat del fluid al punt x. El cabal es defineix com la quantitat de fluid que flueix a través de S en una unitat de temps. Per trobar el cabal, cal calcular el producte escalar de v pel vector unitari normal a la superfície S a cada punt, això donarà un camp escalar, integrant aquest camp escalar sobre la superfície:
El cabal de fluid d'aquest exemple pot ser d'un fluid físic com l'aigua o l'aire, o d'un flux elèctric o magnètic (en aquest cas rep el nom de flux en comptes de cabal). Així les integrals de superfície tenen aplicacions a la física, en particular a la teoria clàssica de l'electromagnetisme. Integrals de formes diferencialsUna forma diferencial és un concepte matemàtic en els camps del càlcul multivariable, topologia diferencial i tensors. La notació moderna de les formes diferencials, així com la idea de les formes diferencials com el producte exterior de derivades exteriors formant un àlgebra exterior, va ser presentada per Élie Cartan. Es comença treballant en un conjunt obert de Rn. Una 0-forma es defineix com una funció infinitament derivable f. Quan s'integra una funció f sobre un subespai de m-dimensional S de Rn, s'escriu com (Els superíndexs són índexs, no exponents) Es pot considerar que dx¹ fins a dxn són objectes formals ells mateixos, més que no pas etiquetes afegides per fer que la integral s'assembli als sumatoris de Riemann. De forma alternativa es poden veure com a covectors, i així una mesura de la "densitat" (per tant integrable en un sentit general). Es diu als dx¹, …,dxn formes diferencials de grau u basiques. Es defineix el producte exterior, "∧", un operador "multiplicació" bilineal sobre aquests elements, amb la propietat alternant de per tots els índexs a. Fixeu-vos que l'alternança juntament amb la linealitat implica dxb∧dxa = −dxa∧dxb. Això també assegura que el resultat del producte exterior té una orientació. Es defineix el conjunt de tots aquests productes com les 2-formes bàsiques, i de forma similar es defineix el conjunt dels productes de la forma dxa∧dxb∧dxc com les 3-formes bàsiques. Una k-forma general és, per tant, una suma ponderada de k-formes, bàsiques on els pesos són les funcions infinitament derivables f. Totes juntes formen un espai vectorial amb les k-formes bàsiques com els vectors base, i les 0-formes (funcions infinitament derivables) com el camp d'escalars. El producte exterior s'estén a les k-formes de la forma natural. Sobre Rn com a màxim n covectors poden ser linealment independents, així una k-forma amb k > n serà sempre zero per la propietat alternant. A més del producte exterior, també hi ha l'operador derivada exterior d. Aquest operador fa correspondre a les k-formes (k+1)-formes. Per una k-forma ω = f dxa sobre Rn, es defineix l'acció de d per: Amb extensió a les k-formes generals de linealment. Aquest plantejament més general permet un enfocament de la integració sobre varietats lliure de coordenades. També permet una generalització natural del teorema fonamental del càlcul, anomenada el teorema de Stokes, que es pot establir com on ω és una k-forma general, i ∂Ω indica la frontera de la regió Ω. Així en el cas que ω és una 0-forma i Ω és un interval tancat de la recta real, el teorema de Stokes es redueix al teorema fonamental del càlcul. En el cas que ω sigui una 1-forma i Ω sigui una regió de dimensió 2 en el pla, el teorema es redueix al teorema de Green. De manera similar, emprant, 2-formes, i 3-formes i la dualitat de Hodge, es pot arribar al teorema de Stokes i al teorema de la divergència. D'aquesta forma es pot veure que les formes diferencials subministren una potent visió unificadora de la integració. Referències i notes
Bibliografia
Vegeu també
Enllaços externs
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia



























































![{\displaystyle \int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}=6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd73b4f0af904c14ed328dffa7434256e9f32eca)
![{\displaystyle {\begin{aligned}\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}&{}=\lim _{s\to 0}\int _{-1}^{-s}{\frac {dx}{\sqrt[{3}]{x^{2}}}}+\lim _{t\to 0}\int _{t}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}\\&{}=\lim _{s\to 0}3(1-{\sqrt[{3}]{s}})+\lim _{t\to 0}3(1-{\sqrt[{3}]{t}})\\&{}=3+3\\&{}=6.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4348fbc3e4bf3a5345fc4c8ca5e93e87307799c)










