Equilibri químic

En una reacció química, l'equilibri químic és l'estat en què tant els reactius com els productes estan presents en concentracions que no tenen més tendència a canviar amb el temps, de manera que no hi ha cap canvi observable en les propietats del sistema.[1] Aquest estat es produeix quan la reacció directa transcorre a la mateixa velocitat que la reacció inversa. Les velocitats de reacció de les reaccions cap endavant i cap enrere generalment no són zero, però són iguals. Així, no hi ha canvis nets en les concentracions dels reactius i productes. Aquest estat es coneix com a equilibri dinàmic.[2][3]

Introducció històrica

El concepte d'equilibri químic es va desenvolupar el 1803, després que Berthollet descobrís que algunes reaccions químiques són reversibles.[Nota 1] Perquè qualsevol mescla de reacció existeixi en equilibri, les velocitats de les reaccions cap endavant (directa) i cap enrere (inversa) han de ser iguals. A l'equació química següent, les fletxes assenyalen les dues maneres per indicar l'equilibri.[Nota 2] A i B són espècies químiques reactives, S i T són espècies de productes, i α, β, σ i τ són els coeficients estequiomètrics dels reactius i productes respectius:

α A + β B σ S + τ T

Es diu que la posició de concentració d'equilibri d'una reacció es troba «extrema a la dreta» si, a l'equilibri, es consumeixen gairebé tots els reactius. Per contra, es diu que la posició d'equilibri és «extrema a l'esquerra» si gairebé no es forma cap producte a partir dels reactius.

Guldberg i Waage (1865), a partir de les idees de Berthollet, va proposar la llei d'acció de masses:

• Velocitat de reacció directa: ${\displaystyle k_{+}{\ce {A}}^{\alpha }{\ce {B}}^{\beta }}$
• Velocitat de reacció inversa: ${\displaystyle k_{-}{\ce {S}}^{\sigma }{\ce {T}}^{\tau }}$

on A, B, S i T són masses actives i k₊ i k₋ són constants de velocitat. Com que a l'equilibri les quantitats cap endavant i cap enrere són iguals:

${\displaystyle k_{+}\left\{{\ce {A}}\right\}^{\alpha }\left\{{\ce {B}}\right\}^{\beta }=k_{-}\left\{{\ce {S}}\right\}^{\sigma }\left\{{\ce {T}}\right\}^{\tau }}$

i la relació de les constants de velocitat també és una constant, ara coneguda com a constant d'equilibri.

${\displaystyle K_{c}={\frac {k_{+}}{k_{-}}}={\frac {\{{\ce {S}}\}^{\sigma }\{{\ce {T}}\}^{\tau }}{\{{\ce {A}}\}^{\alpha }\{{\ce {B}}\}^{\beta }}}}$

Per convenció, els productes formen el numerador.

Tanmateix, la llei d'acció de masses només és vàlida per a reaccions concertades d'un sol pas que passen per un únic estat de transició i no és vàlida en general perquè les equacions cinètiques no segueixen, en general, l'estequiometria de la reacció tal com havien proposat Guldberg i Waage (vegeu, per exemple, substitució nucleòfila aromàtica per S_N1 o reacció d'hidrogen i brom per formar bromur d'hidrogen). Però la igualtat de velocitats de reacció cap endavant i cap enrere és una condició necessària per a l'equilibri químic, encara que no és suficient per explicar per què es produeix l'equilibri.

Malgrat les limitacions d'aquesta derivació, la constant d'equilibri d'una reacció és efectivament una constant, independent de les activitats de les diverses espècies implicades, tot i que depèn de la temperatura tal com s'observa per l'equació de Van 't Hoff. L'addició d'un catalitzador afectarà tant la reacció directa com la reacció inversa de la mateixa manera i no tindrà cap efecte sobre la constant d'equilibri. El catalitzador accelerarà ambdues reaccions augmentant així la velocitat a la qual s'arriba a l'equilibri.[2][4]

Tot i que les concentracions d'equilibri macroscòpic són constants en el temps, les reaccions es produeixen a nivell molecular. Per exemple, en el cas de l'àcid acètic dissolt en aigua i formant ions acetat i d'hidroni,

CH₃CO₂H + H₂O ⇌ CH
3CO−
2 + H₃O^+

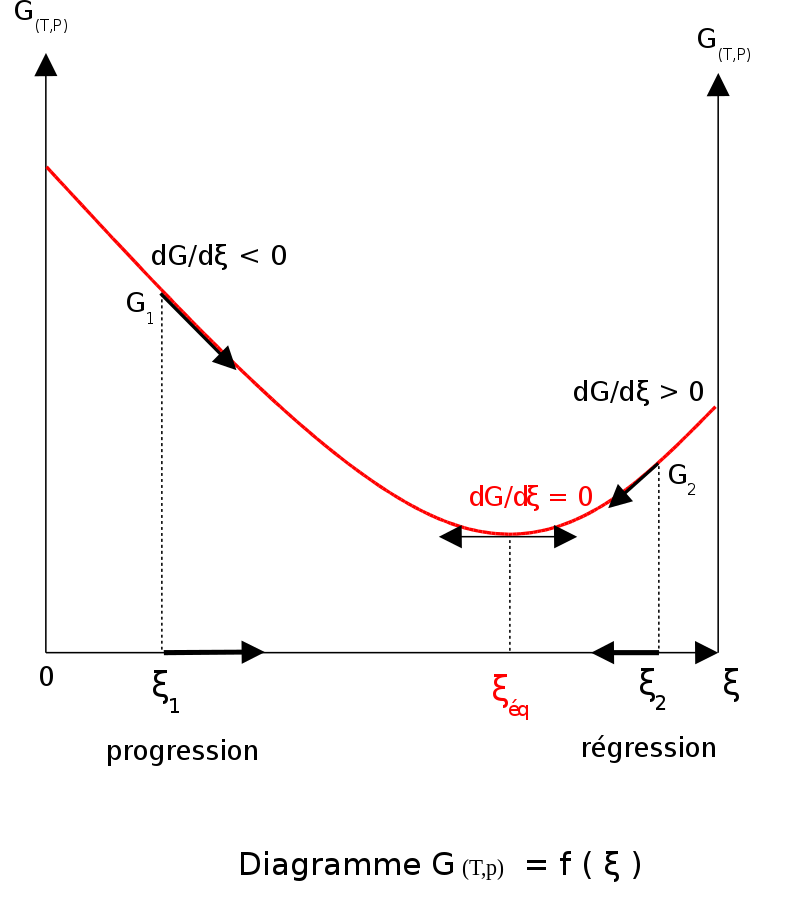
un protó pot saltar d'una molècula d'àcid acètic a una molècula d'aigua i després a un anió d'acetat per formar una altra molècula d'àcid acètic i deixant el nombre de molècules d'àcid acètic sense canvis. Aquest és un exemple d'equilibri dinàmic. Els equilibris, com la resta de la termodinàmica, són fenòmens estadístics, mitjanes de comportament microscòpic.

El principi de Le Châtelier (1884) prediu el comportament d'un sistema d'equilibri quan es produeixen canvis en les seves condicions de reacció. Si un equilibri dinàmic es veu alterat pel canvi de les condicions, la posició d'equilibri es mou per invertir parcialment el canvi. Per exemple, afegir més S des de l'exterior provocarà un excés de productes, i el sistema intentarà contrarestar-ho augmentant la reacció inversa i empenyent el punt d'equilibri cap enrere (tot i que la constant d'equilibri es mantindrà igual).

Si s'afegeix àcid mineral a la barreja d'àcid acètic, augmentant la concentració d'ió hidroni, la quantitat de dissociació ha de disminuir a mesura que la reacció es mou cap a l'esquerra d'acord amb aquest principi. Això també es pot deduir de l'expressió constant d'equilibri de la reacció:

${\displaystyle K={\frac {\{{\ce {CH3CO2-}}\}\{{\ce {H3O+}}\}}{{\ce {\{CH3CO2H\}}}}}}$

Si {H₃O+} augmenta, {CH₃CO₂H} ha d'augmentar i CH
3CO−
2 ha de disminuir. L'H₂O es deixa fora, ja que és el dissolvent i la seva concentració es manté alta i gairebé constant.

Una versió quantitativa ve donada pel quocient de reacció.

J. W. Gibbs va suggerir el 1873 que l'equilibri s'aconsegueix quan l'energia lliure de Gibbs del sistema és al seu valor mínim (suposant que la reacció es porta a terme a una temperatura i pressió constants). Això vol dir que la derivada de l'energia de Gibbs respecte a la coordenada de reacció (una mesura del grau d'avançament d'una reacció que s'ha produït, que va des de zero per a tots els reactius fins a un màxim per a tots els productes) s'esvaeix, indicant un punt estacionari. Aquesta derivada s'anomena energia de Gibbs de reacció (o canvi d'energia) i correspon a la diferència entre els potencials químics dels reactius i els productes en la composició de la mescla de reacció.[1] Aquest criteri és alhora necessari i suficient. Si una mescla no està en equilibri, l'alliberament de l'excés d'energia de Gibbs (o energia de Helmholtz en reaccions de volum constant) és la «força motriu» perquè la composició de la mescla canviï fins que s'arribi a l'equilibri. La constant d'equilibri es pot relacionar amb el canvi d'energia lliure de Gibbs estàndard per a la reacció mitjançant l'equació

${\displaystyle \Delta _{r}G^{\ominus }=-RT\ln K_{\mathrm {eq} }}$

on R és la constant universal del gas i T la temperatura.

Quan els reactius es dissolen en un medi d'alta força iònica, el quocient dels coeficients d'activitat es pot considerar constant. En aquest cas, el quocient de concentració, K_c,

${\displaystyle K_{\ce {c}}={\frac {[{\ce {S}}]^{\sigma }[{\ce {T}}]^{\tau }}{[{\ce {A}}]^{\alpha }[{\ce {B}}]^{\beta }}}}$

on [A] és la concentració d'A, etc., és independent de la concentració analítica dels reactius. Per aquesta raó, les constants d'equilibri de les solucions es solen determinar en medis d'alta força iònica. K_c varia amb la força iònica, la temperatura i la pressió (o volum). De la mateixa manera, K_p per als gasos depèn de la pressió parcial. Aquestes constants són més fàcils de mesurar i de trobar-se als cursos de química de batxillerat.

Termodinàmica

A temperatura i pressió constants, cal considerar l'energia lliure de Gibbs, G, mentre que a temperatura i volum constants, cal considerar l'energia lliure de Helmholtz, A, per a la reacció; i a energia i volum interns constants, cal tenir en compte l'entropia, S, de la reacció.

El cas de volum constant és important en geoquímica i química atmosfèrica on les variacions de pressió són significatives. S'ha de tenir en compte que, si els reactius i els productes estiguessin en estat estàndard (completament pur), llavors no hi hauria reversibilitat ni equilibri. De fet, necessàriament ocuparien volums d'espai disjunts. La barreja dels productes i reactius contribueix a un gran augment d'entropia (conegut com a entropia de mescla) als estats que contenen una barreja igual de productes i reactius i dona lloc a un mínim distintiu en l'energia de Gibbs en funció de l'extensió de la reacció.[5] El canvi d'energia de Gibbs estàndard, juntament amb l'energia de Gibbs de la mescla, determinen l'estat d'equilibri.[6][7]

En aquest article només es considera el cas de «pressió constant». La relació entre l'energia lliure de Gibbs i la constant d'equilibri es pot trobar considerant potencials químics.[1]

A temperatura i pressió constants en absència d'una tensió aplicada, l'energia lliure de Gibbs, G, per a la reacció depèn només del grau d'avançament d'una reacció: ξ (lletra grega ksi), i només pot disminuir segons la segona llei de la termodinàmica. Vol dir que la derivada de G respecte a ξ ha de ser negativa si es produeix la reacció; a l'equilibri aquesta derivada és igual a zero.

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=0~}$:     equilibri

Per tal de complir la condició termodinàmica d'equilibri, l'energia de Gibbs ha de ser estacionària, és a dir, la derivada de G respecte al grau d'avançament d'una reacció, ξ, ha de ser zero. Es pot demostrar que en aquest cas, la suma dels potencials químics multiplicada per els coeficients estequiomètrics dels productes és igual a la suma dels corresponents als reactius.[8] Per tant, la suma de les energies de Gibbs dels reactius ha de ser igual a la suma de les energies de Gibbs dels productes.

${\displaystyle \alpha \mu _{\mathrm {A} }+\beta \mu _{\mathrm {B} }=\sigma \mu _{\mathrm {S} }+\tau \mu _{\mathrm {T} }\,}$

on μ és en aquest cas una energia de Gibbs molar parcial, un potencial químic. El potencial químic d'un reactiu A és una funció de l'activitat, {A} d'aquest reactiu.

${\displaystyle \mu _{\mathrm {A} }=\mu _{A}^{\ominus }+RT\ln\{\mathrm {A} \}\,}$

(on μo
A és el potencial químic estàndard).

La definició de l'equació d'energia de Gibbs interacciona amb la relació fonamental de la termodinàmica per produir

${\displaystyle dG=Vdp-SdT+\sum _{i=1}^{k}\mu _{i}dN_{i}}$.

Afegint dN_i = ν_i dξ a l'equació anterior dona un coeficient estequiomètric (${\displaystyle \nu _{i}~}$) i un diferencial que denota la reacció que es produeix en una mesura infinitesimal (dξ). A pressió i temperatura constants, les equacions anteriors es poden escriure com

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\sum _{i=1}^{k}\mu _{i}\nu _{i}=\Delta _{\mathrm {r} }G_{T,p}}$ que és el canvi d'energia lliure de Gibbs per a la reacció.

Això resulta en:

${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=\sigma \mu _{\mathrm {S} }+\tau \mu _{\mathrm {T} }-\alpha \mu _{\mathrm {A} }-\beta \mu _{\mathrm {B} }\,}$.

Substituint els potencials químics:

${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=(\sigma \mu _{\mathrm {S} }^{\ominus }+\tau \mu _{\mathrm {T} }^{\ominus })-(\alpha \mu _{\mathrm {A} }^{\ominus }+\beta \mu _{\mathrm {B} }^{\ominus })+(\sigma RT\ln\{\mathrm {S} \}+\tau RT\ln\{\mathrm {T} \})-(\alpha RT\ln\{\mathrm {A} \}+\beta RT\ln\{\mathrm {B} \})}$,

la relació esdevé:

${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=\sum _{i=1}^{k}\mu _{i}^{\ominus }\nu _{i}+RT\ln {\frac {\{\mathrm {S} \}^{\sigma }\{\mathrm {T} \}^{\tau }}{\{\mathrm {A} \}^{\alpha }\{\mathrm {B} \}^{\beta }}}}$

${\displaystyle \sum _{i=1}^{k}\mu _{i}^{\ominus }\nu _{i}=\Delta _{\mathrm {r} }G^{\ominus }}$:

que és el «canvi d'energia estàndard de Gibbs per a la reacció» que es pot calcular mitjançant taules termodinàmiques.

El quocient de reacció es defineix com:

${\displaystyle Q_{\mathrm {r} }={\frac {\{\mathrm {S} \}^{\sigma }\{\mathrm {T} \}^{\tau }}{\{\mathrm {A} \}^{\alpha }\{\mathrm {B} \}^{\beta }}}}$

Per tant,

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G_{T,p}=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln Q_{\mathrm {r} }}$

En equilibri:

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G_{T,p}=0}$

que condueix a:

${\displaystyle 0=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln K_{\mathrm {eq} }}$

i

${\displaystyle \Delta _{\mathrm {r} }G^{\ominus }=-RT\ln K_{\mathrm {eq} }}$

L'obtenció del valor del canvi d'energia estàndard de Gibbs, permet calcular la constant d'equilibri.

• 
  Corba de variació de G(T,p) en funció de ξ; equilibri químic

Addició de reactius o productes

Per a un sistema reaccional en equilibri: Q_r = K_eq; ξ = ξ_eq.

• Si es modifiquen les activitats dels components, el valor del quocient de reacció canvia i esdevé diferent de la constant d'equilibri: Q_r ≠ K_eq.

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln Q_{\mathrm {r} }~}$

i

${\displaystyle \Delta _{\mathrm {r} }G^{\ominus }=-RT\ln K_{eq}~}$

llavors

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=RT\ln \left({\frac {Q_{\mathrm {r} }}{K_{\mathrm {eq} }}}\right)~}$

• Si l'activitat d'un reactiu i augmenta

${\displaystyle Q_{\mathrm {r} }={\frac {\prod (a_{j})^{\nu _{j}}}{\prod (a_{i})^{\nu _{i}}}}~,}$

el quocient de reacció disminueix. Aleshores

${\displaystyle Q_{\mathrm {r} }<K_{\mathrm {eq} }~}$

i

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}<0~}$

La reacció es desplaçarà cap a la dreta (és a dir, en direcció cap endavant i, per tant, es formaran més productes).

• Si l'activitat d'un producte j augmenta, aleshores

${\displaystyle Q_{\mathrm {r} }>K_{\mathrm {eq} }~}$

i

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}>0~}$

La reacció es desplaçarà cap a l'esquerra (és a dir, en sentit invers i, per tant, es formaran menys productes).

Tingueu en compte que les activitats i les constants d'equilibri són nombres adimensionals.

Tractament de l'activitat

L'expressió de la constant d'equilibri es pot reescriure com el producte d'un quocient de concentració, K_c, i d'un quocient de coeficient d'activitat, Γ.

${\displaystyle K={\frac {[\mathrm {S} ]^{\sigma }[\mathrm {T} ]^{\tau }...}{[\mathrm {A} ]^{\alpha }[\mathrm {B} ]^{\beta }...}}\times {\frac {{\gamma _{\mathrm {S} }}^{\sigma }{\gamma _{\mathrm {T} }}^{\tau }...}{{\gamma _{\mathrm {A} }}^{\alpha }{\gamma _{\mathrm {B} }}^{\beta }...}}=K_{\mathrm {c} }\Gamma }$

[A] és la concentració del reactiu A, etc. En principi és possible obtenir valors dels coeficients d'activitat, γ. Per a les solucions, es poden utilitzar equacions com l'equació de Debye-Hückel o extensions com l'equació de Davies[9] o la teoria específica de la interacció iònica, o equacions de Pitzer.[10]

Tanmateix, això no sempre és possible. És pràctica habitual assumir que Γ és una constant i utilitzar el quocient de concentració en lloc de la constant d'equilibri termodinàmic. També és pràctica general utilitzar el terme constant d'equilibri en lloc del quocient de concentració més precís. Aquesta pràctica es seguirà aquí.

Per a reaccions en fase gasosa s'utilitza la pressió parcial en lloc de la concentració i el coeficient de fugacitat en lloc del coeficient d'activitat. En el món real, per exemple, quan es fa amoníac a la indústria, s'han de tenir en compte els coeficients de fugacitat. La fugacitat, f, és el producte de la pressió parcial i el coeficient de fugacitat. El potencial químic d'una espècie en fase gasosa real ve donat per

${\displaystyle \mu =\mu ^{\ominus }+RT\ln \left({\frac {f}{\mathrm {bar} }}\right)=\mu ^{\ominus }+RT\ln \left({\frac {p}{\mathrm {bar} }}\right)+RT\ln \gamma }$

per tant, l'expressió general que defineix una constant d'equilibri és vàlida tant per a la fase de solució com per a la fase gasosa.

Quocients de concentració

En solució aquosa, les constants d'equilibri es determinen normalment en presència d'un electròlit «inert» com el nitrat de sodi, NaNO₃, o el perclorat de potassi, KClO₄. La força iònica d'una solució ve donada per

${\displaystyle I={\frac {1}{2}}\sum _{i=1}^{N}c_{i}z_{i}^{2}}$

on c_i i z_i representen la concentració i la càrrega iònica de l'ió tipus i, i la suma es pren sobre tots els N tipus d'espècies carregades en solució. Quan la concentració de sal dissolta és molt superior a les concentracions analítiques dels reactius, els ions originats de la sal dissolta determinen la força iònica i la força iònica és efectivament constant. Com que els coeficients d'activitat depenen de la força iònica, els coeficients d'activitat de l'espècie són efectivament independents de la concentració. Per tant, es justifica la suposició que Γ és constant. El quocient de concentració és un múltiple simple de la constant d'equilibri.[11]

${\displaystyle K_{\mathrm {c} }={\frac {K}{\Gamma }}}$

Tanmateix, K_c variarà amb la força iònica. Si es mesura a una sèrie de forces iòniques diferents, el valor es pot extrapolar a la força iònica zero.[10] El quocient de concentració obtingut d'aquesta manera es coneix, paradoxalment, com a constant d'equilibri termodinàmic.

Abans d'utilitzar un valor publicat d'una constant d'equilibri en condicions de força iònica diferents de les condicions utilitzades en la seva determinació, s'ha d'ajustar el valor.

Mescles metaestables

Una mescla pot semblar que no té tendència a canviar, tot i que no està en equilibri. Per exemple, una barreja de SO₂ i O₂ és metaestable ja que hi ha una barrera cinètica a la formació del producte, SO₃.

2 SO₂ + O₂ 2 SO₃

La barrera es pot superar quan un catalitzador també està present a la mescla com en el procés de contacte, però el catalitzador no afecta les concentracions d'equilibri.

Així mateix, la formació de bicarbonat a partir del diòxid de carboni i l'aigua és molt lenta en condicions normals

CO₂ + 2 H₂O HCO−
3 + H₃O^+

però gairebé instantània en presència de l'enzim catalític anhidrasa carbònica.

Substàncies pures

Quan en els equilibris intervenen substàncies pures (líquids o sòlids) les seves activitats no apareixen en la constant d'equilibri[12] perquè els seus valors numèrics es consideren un.

Aplicant la fórmula general d'una constant d'equilibri al cas específic d'una solució diluïda d'àcid acètic en aigua s'obté

CH₃CO₂H + H₂O CH₃CO₂^− + H₃O^+

${\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}][{H_{2}O}]} }}}$

Per a totes les solucions excepte les molt concentrades, l'aigua es pot considerar un líquid «pur» i, per tant, té una activitat d'un. Per tant, l'expressió constant d'equilibri s'escriu normalment com

${\displaystyle K={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}]} }}=K_{\mathrm {c} }}$.

Un cas particular és l'autoionització de l'aigua

2 H₂O H₃O^+ + OH^−

Com que l'aigua és el dissolvent i té una activitat d'un, la constant d'autoionització de l'aigua es defineix com

${\displaystyle K_{\mathrm {w} }=\mathrm {[H^{+}][OH^{-}]} }$

És perfectament legítim escriure [H^+] per a la concentració d'ions hidroni, ja que l'estat de solvatació del protó és constant (en solucions diluïdes) i, per tant, no afecta les concentracions d'equilibri. K_w varia amb la variació de la força iònica i/o la temperatura.

Les concentracions de H^+ i OH^− no són magnituds independents. Amb més freqüència, [OH^−] es substitueix per K_w[H^+]^−1 en expressions constants d'equilibri que, d'altra manera, inclourien ions hidròxid.

Els sòlids tampoc no apareixen en l'expressió constant d'equilibri, si es considera que són purs i, per tant, les seves activitats són considerades una. Un exemple és la reacció de Boudouard:[12]

2 CO CO₂ + C

per a la qual l'equació (sense carboni sòlid) s'escriu com:

${\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[CO_{2}]} }{\mathrm {[CO]^{2}} }}}$

Equilibris múltiples

Considereu el cas d'un àcid dibàsic H₂A. Quan es dissol en aigua, la mescla contindrà H₂A, HA^− i A^2−. Aquest equilibri es pot dividir en dos passos en cadascun dels quals s'allibera un protó.

${\displaystyle {\begin{array}{rl}{\ce {H2A <=> HA^- + H+}}:&K_{1}={\frac {{\ce {[HA-][H+]}}}{{\ce {[H2A]}}}}\\{\ce {HA- <=> A^2- + H+}}:&K_{2}={\frac {{\ce {[A^{2-}][H+]}}}{{\ce {[HA-]}}}}\end{array}}}$

K₁ i K₂ són exemples de constants d'equilibri parcials. La constant d'equilibri global, β_D, és el producte de les constants d'equilibri parcials.

${\displaystyle {\ce {{H2A}<=>{A^{2-}}+{2H+}}}}$:     ${\displaystyle \beta _{{\ce {D}}}={\frac {{\ce {[A^{2-}][H^+]^2}}}{{\ce {[H_2A]}}}}=K_{1}K_{2}}$

Tingueu en compte que aquestes constants són constants de dissociació perquè els productes del costat dret de l'expressió d'equilibri són productes de dissociació. En molts sistemes, és preferible utilitzar constants d'associació.

${\displaystyle {\begin{array}{ll}{\ce {A^2- + H+ <=> HA-}}:&\beta _{1}={\frac {{\ce {[HA^-]}}}{{\ce {[A^{2-}][H+]}}}}\\{\ce {A^2- + 2H+ <=> H2A}}:&\beta _{2}={\frac {{\ce {[H2A]}}}{{\ce {[A^{2-}][H+]^2}}}}\end{array}}}$

β₁ i β₂ són exemples de constants d'associació. Clarament β₁ = 1/K₂ i β₂ = 1/β_D; log β₁ = pK₂ i log β₂ = pK₂ + pK₁[13]

Per a sistemes d'equilibri múltiples, vegeu també: teoria de les reaccions de resposta.

Efecte de la temperatura

L'efecte del canvi de temperatura sobre una constant d'equilibri ve donat per l'equació de Van 't Hoff

${\displaystyle {\frac {d\ln K}{dT}}={\frac {\Delta H_{\mathrm {m} }^{\ominus }}{RT^{2}}}}$

Així, per a les reaccions exotèrmiques (ΔH < 0), K disminueix amb l'augment de la temperatura, però, per a les reaccions endotèrmiques, (ΔH > 0) K augmenta amb l'augment de la temperatura. Una formulació alternativa és

${\displaystyle {\frac {d\ln K}{d(T^{-1})}}=-{\frac {\Delta H_{\mathrm {m} }^{\ominus }}{R}}}$

A primera vista, això sembla oferir un mitjà per obtenir l'entalpia molar estàndard de la reacció estudiant la variació de K amb la temperatura. Però a la pràctica el mètode no és fiable perquè la propagació d'errors gairebé sempre dona errors molt grans en els valors calculats d'aquesta manera.

Efecte dels camps elèctrics i magnètics

L'efecte del camp elèctric en l'equilibri ha estat estudiat per Manfred Eigen,[14][15] entre d'altres.

Tipus d'equilibri

Procés de Haber-Bosch

1. N₂ (g) N₂ (adsorbit)
2. N₂ (adsorbit) 2 N (adsorbit)
3. H₂ (g) H₂ (adsorbit)
4. H₂ (adsorbit) 2 H (adsorbit)
5. N (adsorbit) + 3 H(adsorbit) NH₃ (adsorbit)
6. NH₃ (adsorbit) NH₃ (g)

L'equilibri es pot classificar a grans trets com a equilibri heterogeni i homogeni.[16] L'equilibri homogeni consisteix en reactius i productes que pertanyen a la mateixa fase, mentre que l'equilibri heterogeni entra en joc per a reactius i productes en diferents fases.

• En fase gasosa: motors de coets.[17]
• La síntesi industrial com l'amoníac en el procés de Haber-Bosch (representat a la dreta) té lloc mitjançant una successió d'etapes d'equilibri que inclouen processos d'adsorció.
• Química atmosfèrica.
• Aigua de mar i altres aigües naturals: oceanografia química.
• Distribució entre dues fases:
  • coeficient de distribució log D: important per a productes farmacèutics on la lipofilia és una propietat significativa d'un fàrmac.
  • extracció líquid-líquid, bescanvi iònic, cromatografia.
  • producte de solubilitat.
  • absorció i alliberament d'oxigen per part de l'hemoglobina a la sang.
• Equilibri àcid-base: constant d'acidesa, hidròlisi, dissolució amortidora, indicadors de pH, homeòstasi acidobàsica.
• Complexació metall-lligant: agents segrestadors, teràpia de quelació, reactius de contrast per ressonància magnètica, equilibri de Schlenk.
• Formació d'adductes: química hoste-hoste, química supramolecular, reconeixement molecular, tetròxid de dinitrogen.
• En determinades reaccions oscil·lants, l'aproximació a l'equilibri no és asimptòtica sinó en forma d'oscil·lació amortida.
• L'equació de Nernst relacionada en electroquímica dona la diferència de potencial de l'elèctrode en funció de les concentracions redox.
• Quan les molècules a cada costat de l'equilibri són capaces de reaccionar encara més de manera irreversible en reaccions secundàries, la relació de producte final es determina segons el principi de Curtin-Hammett.

En aquestes aplicacions s'utilitzen termes com ara «constant d'estabilitat», «constant de formació», «constant d'enllaç», «constant d'afinitat», «constant d'associació» i «constant de dissociació». En bioquímica, és habitual donar unitats per a «constants d'unió», que serveixen per definir les unitats de concentració utilitzades quan es va determinar el valor de la constant.

Composició d'una mescla

Quan l'únic equilibri és el de la formació d'un adducte 1:1 com a composició d'una mescla, hi ha moltes maneres de calcular la composició d'una mescla. Per exemple, vegeu la taula ICE per obtenir un mètode tradicional per calcular el pH d'una solució d'àcid feble.

Hi ha tres enfocaments per al càlcul general de la composició d'una mescla en equilibri.

1. L'enfocament més bàsic és manipular les diferents constants d'equilibri fins que les concentracions desitjades s'expressin en termes de constants d'equilibri mesurades (equivalent a mesurar potencials químics) i condicions inicials.
2. Minimitzar l'energia de Gibbs del sistema.[18][19]
3. Satisfer l'equació del balanç de matèria. Les equacions de balanç de masses són simplement afirmacions que demostren que la concentració total de cada reactiu ha de ser constant per la llei de conservació de la massa.

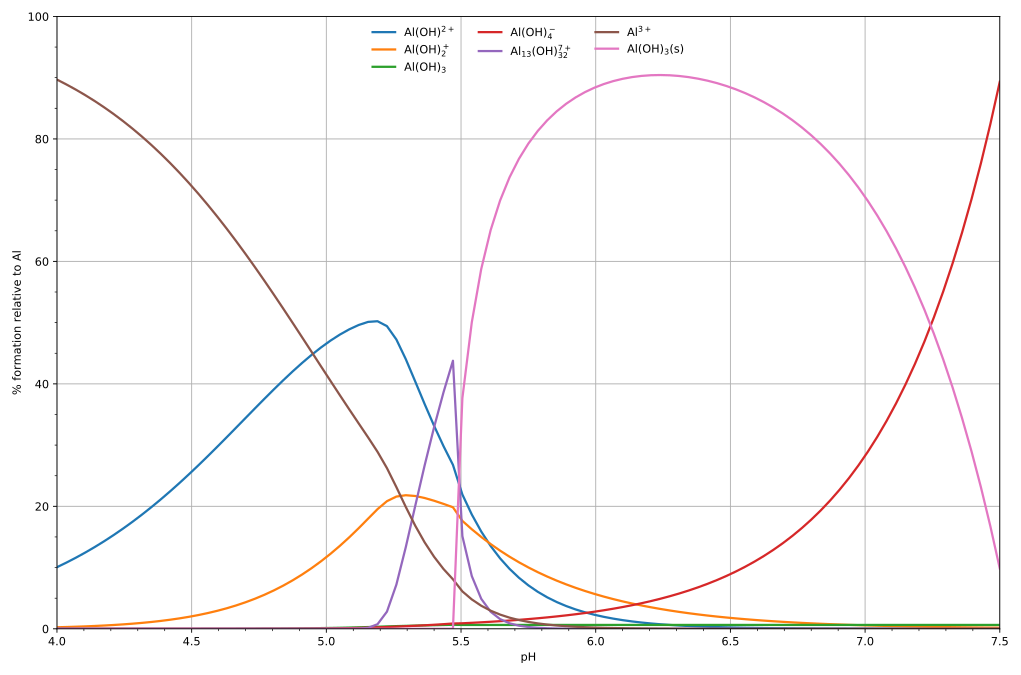
Equacions de balanç de massa

En general, els càlculs són força complicats o complexos. Per exemple, en el cas d'un àcid dibàsic, H₂A dissolt en aigua, els dos reactius es poden especificar com la base conjugada, A^2−, i el protó, H^+. Les següents equacions de balanç de masses podrien aplicar-se igualment bé a una base com l'1,2-diaminoetà, en aquest cas la base mateixa es designa com a reactiu A:

${\displaystyle T_{\mathrm {A} }=\mathrm {[A]+[HA]+[H_{2}A]} \,}$

${\displaystyle T_{\mathrm {H} }=\mathrm {[H]+[HA]+2[H_{2}A]-[OH]} \,}$

amb T_A la concentració total de l'espècie A. Tingueu en compte que és costum ometre les càrregues iòniques en escriure i utilitzar aquestes equacions.

Quan es coneixen les constants d'equilibri i s'especifiquen les concentracions totals, hi ha dues equacions en dues «concentracions lliures» desconegudes [A] i [H]. Això es dedueix del fet que [HA] = β₁[A][H], [H₂A] = β₂[A][H]^2 i [OH] = K_w[H]^−1

${\displaystyle T_{\mathrm {A} }=\mathrm {[A]} +\beta _{1}\mathrm {[A][H]} +\beta _{2}\mathrm {[A][H]} ^{2}\,}$

${\displaystyle T_{\mathrm {H} }=\mathrm {[H]} +\beta _{1}\mathrm {[A][H]} +2\beta _{2}\mathrm {[A][H]} ^{2}-K_{w}[\mathrm {H} ]^{-1}\,}$

per tant, les concentracions dels «complexes» es calculen a partir de les concentracions lliures i de les constants d'equilibri.

Les expressions generals aplicables a tots els sistemes amb dos reactius, A i B serien

${\displaystyle T_{\mathrm {A} }=[\mathrm {A} ]+\sum _{i}p_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}$

${\displaystyle T_{\mathrm {B} }=[\mathrm {B} ]+\sum _{i}q_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}$

És fàcil veure com això es pot estendre a tres o més reactius.

Àcids polibàsics

La composició de les solucions que contenen reactius A i H és fàcil de calcular en funció de p[H]. Quan es coneix [H], la concentració lliure [A] es calcula a partir de l'equació de balanç de massa en A.

El diagrama de la part inferior mostra un exemple de la hidròlisi àcid de Lewis d'alumini Al^3+_(aq) [Nota 3] mostra les concentracions d'espècies per a una solució 5 × 10^−6 M d'una sal d'alumini en funció del pH. Cada concentració es mostra com a percentatge del total d'alumini.

• 
  Concentracions d'espècies durant la hidròlisi de l'alumini

Dissolució i precipitació

El diagrama anterior il·lustra el punt que es pot formar un precipitat que no és una de les espècies principals en l'equilibri de la solució. A pH just per sota de 5,5, les principals espècies presents en una solució 5 μM d'Al^3+ són hidròxids d'alumini Al(OH)^2+, AlOH+
2 i Al
13(OH)7+
32, però en augmentar el pH Al(OH)₃ precipita de la solució.

Això passa perquè Al(OH)₃ té una energia reticular molt gran. A mesura que el pH augmenta, cada cop sorgeix més Al(OH)₃ de la solució. Aquest és un exemple del principi de Le Châtelier en acció: augmentar la concentració de l'ió hidròxid fa que precipiti més hidròxid d'alumini, que elimina l'hidròxid de la solució. Quan la concentració d'hidròxid és prou alta es forma l'aluminat soluble, Al(OH)^−4.

Un altre cas comú on es produeix la precipitació és quan un catió metàl·lic interacciona amb un lligand aniònic per formar un complex elèctricament neutre. Si el complex és hidròfob, precipitarà fora de l'aigua. Això passa amb l'ió níquel Ni^2+ i la dimetilglioxima, (dmgH₂): en aquest cas l'energia reticular del sòlid no és especialment gran, però supera molt l'energia de solvatació de la molècula Ni(dmgH)₂.

Minimització de l'energia de Gibbs

A l'equilibri, a una temperatura i pressió especificades, i sense forces externes, l'energia lliure de Gibbs G és com a mínim:

${\displaystyle dG=\sum _{j=1}^{m}\mu _{j}\,dN_{j}=0}$

on μj és el potencial químic de l'espècie molecular j, i Nj és la quantitat d'espècie molecular j. Es pot expressar en termes d'activitat termodinàmica com:

${\displaystyle \mu _{j}=\mu _{j}^{\ominus }+RT\ln {A_{j}}}$

on ${\displaystyle \mu _{j}^{\ominus }}$ és el potencial químic en estat estàndard, R és la constant del gas T és la temperatura absoluta i Aj és l'activitat.

Per a un sistema tancat, cap partícula no pot entrar ni sortir, tot i que es poden combinar de diverses maneres. El nombre total d'àtoms de cada element es mantindrà constant. Això vol dir que la minimització anterior s'ha de sotmetre a les restriccions:

${\displaystyle \sum _{j=1}^{m}a_{ij}N_{j}=b_{i}^{0}}$

on a_ij és el nombre d'àtoms de l'element i a la molècula j i b0
i és el nombre total d'àtoms de l'element i, que és una constant, ja que el sistema és tancat. Si hi ha un total de k tipus d'àtoms al sistema, llavors hi haurà k d'aquestes equacions. Si hi ha ions implicats, s'afegeix una fila addicional a la matriu a_ij especificant la càrrega respectiva de cada molècula que sumarà zero.

Aquest és un problema estàndard d'optimització, conegut com a minimització restringida. El mètode més comú per resoldre'l és utilitzar el mètode dels multiplicadors de Lagrange[17][20] (tot i que es poden utilitzar altres mètodes).

Definim:

${\displaystyle {\mathcal {G}}=G+\sum _{i=1}^{k}\lambda _{i}\left(\sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{0}\right)=0}$

on els λi són els multiplicadors de Lagrange, un per a cada element. Això permet tractar cadascun dels Nj i λj de manera independent, i es pot demostrar mitjançant les eines de càlcul multivariant que la condició d'equilibri ve donada per

${\displaystyle 0={\frac {\partial {\mathcal {G}}}{\partial N_{j}}}=\mu _{j}+\sum _{i=1}^{k}\lambda _{i}a_{ij}}$

${\displaystyle 0={\frac {\partial {\mathcal {G}}}{\partial \lambda _{i}}}=\sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{0}}$

(Per a la prova, vegeu multiplicadors de Lagrange).

Aquest és un conjunt d'equacions (m + k) en (m + k) incògnites (N_j i λ_i) i, per tant, es pot resoldre per a les concentracions d'equilibri N_j sempre que les activitats químiques es coneguin com a funcions de les concentracions a la temperatura i pressió donades (En el cas ideal, les activitats són proporcionals a les concentracions; Vegeu bases de dades termodinàmiques per a substàncies pures). S'ha de tenir compte que la segona equació és només les restriccions inicials per a la minimització.

Aquest mètode de càlcul de concentracions químiques d'equilibri és útil per a sistemes amb un gran nombre de molècules diferents. L'ús de k equacions de conservació d'elements atòmics per a la restricció de massa és senzill i substitueix l'ús de les equacions de coeficients estequiomètrics.[17] Els resultats són coherents amb els especificats per equacions químiques. Per exemple, si l'equilibri s'especifica mitjançant una única equació química:[21]

${\displaystyle \sum _{j=0}^{m}\nu _{j}R_{j}=0}$

on ν_j és el coeficient estequiomètric de la j-èssima molècula (negatiu per als reactius, positiu per als productes) i R_j és el símbol de la j-èssima molècula, una equació correctament equilibrada obeirà:

${\displaystyle \sum _{j=1}^{m}a_{ij}\nu _{j}=0}$

Multiplicant la primera condició d'equilibri per ν_j i utilitzant l'equació anterior s'obté:

${\displaystyle 0=\sum _{j=1}^{m}\nu _{j}\mu _{j}+\sum _{j=1}^{m}\sum _{i=1}^{k}\nu _{j}\lambda _{i}a_{ij}=\sum _{j=1}^{m}\nu _{j}\mu _{j}}$

Com a dalt, definint ΔG

${\displaystyle \Delta G=\sum _{j=1}^{m}\nu _{j}\mu _{j}=\sum _{j=1}^{m}\nu _{j}(\mu _{j}^{\ominus }+RT\ln(\{R_{j}\}))=\Delta G^{\ominus }+RT\ln \left(\prod _{j=1}^{m}\{R_{j}\}^{\nu _{j}}\right)=\Delta G^{\ominus }+RT\ln(K_{c})}$

on K_c és la constant d'equilibri i ΔG serà zero en equilibri.

Existeixen procediments anàlegs per a la minimització d'altres potencials termodinàmics.[17]

Notes

1. Berthollet, C. L.. Essai de statique chimique (en francès). París: Firmin Didot, 1803, p. 404–407.  Berthellot esmenta que quan va acompanyar Napoleó en la seva expedició a Egipte, ell (Berthellot) va visitar el llac Natron i va trobar carbonat de sodi a les seves ribes. Es va adonar que això era producte de la reacció inversa de la habitual Na₂CO₃ + CaCl₂ → 2NaCl + CaCO₃↓ i, per tant, que l'estat final d'una reacció era un estat d'equilibri entre dos processos oposats. De la pàgina 405: «... la décomposition du muriate de soude continue donc jusqu'à ce qu'il se soit formé assez de muriate de chaux, parce que l'acide muriatique devant se partager entre les deux bases en raison de leur action, il arrive un terme où leurs forces se balancent.» (... la descomposició del clorur de sodi continua així fins que es forma prou clorur de calci, perquè l'àcid clorhídric s'ha de compartir entre les dues bases en la proporció de la seva acció [és a dir, capacitat de reacció]; arriba a un [punt] final en què les seves forces s'equilibren.)
2. La notació va ser proposada el 1884 pel químic holandès Jacobus Henricus van 't Hoff. Vegeu: van 't Hoff, J.H.. Études de Dynamique Chemique (en francès). Amsterdam: Frederik Muller & Co., 1884, p. 4–5.  Van 't Hoff va anomenar «reaccions limitades» les reaccions que no es van completar. De les pàgines 4–5: «Or M. Pfaundler a relié ces deux phénomênes ... s'accomplit en même temps dans deux sens opposés.» (Ara el Sr. Pfaundler ha unit aquests dos fenòmens en un únic concepte en considerar el límit observat com el resultat de dues reaccions oposades, impulsant la de l'exemple citat a la formació de sal marina [és a dir, NaCl] i àcid nítric, i l'altre a l'àcid clorhídric i el nitrat de sodi. Aquesta consideració, que valida l'experiment, justifica l'expressió «equilibri químic», que s'utilitza per caracteritzar l'estat final de les reaccions limitades. Proposaria traduir aquesta expressió pel símbol següent:

   HCl + NO₃ Na NO₃ H + Cl Na.

   Així substitueixo, en aquest cas, el signe = de l'equació química pel signe , que en realitat no expressa només la igualtat sinó que també mostra la direcció de la reacció. Això expressa clarament que una acció química es produeix simultàniament en dues direccions oposades.)
3. El diagrama es va crear amb el programa HySS

Referències

1. Atkins i De Paula, 2006, p. 200-202.
2. Atkins i Loretta, 2008.
3. IUPAC, Compendium of Chemical Terminology, 2a ed. ("The Gold Book") (1997). Versió corregida en línia:  (2006–) "chemical equilibrium" (en anglès).
4. Brady, 2004.
5. Atkins, de Paula i Friedman, 2014, p. Fig. 73.2.
6. Schultz, 1999, p. 1391.
7. Clugston, 1990, p. 203.
8. Mortimer, 2008, p. 305.
9. Davies, 1962.
10. Grenthe, I.; Wanner, H. «Guidelines for the extrapolation to zero ionic strength» ( PDF) (en anglès). OECD Nuclear Energy Agency. Arxivat de l'original el 2008-12-17. [Consulta: 4 setembre 2022].
11. Rossotti i Rossotti, 1961.
12. Eagleson, Mary. «Biochemistry (2nd Ed.)». A: Concise Encyclopedia Chemistry, 1994. ISBN 0-89925-457-8. 
13. Beck i Nagypál, 1990.
14. «The Nobel Prize in Chemistry 1967» (en anglès). Nobel Prize.
15. Eigen, Manfred. «Immeasurably fast reactions» ( PDF) (en anglès). Nobel Prize, 11-12-1967.
16. «Equilibrium constants - Kc» (en anglès). Chemguide.
17. Gordon, Sanford; McBride, Bonnie J. «Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications» ( PDF) (en anglès). NASA, 1994. Arxivat de l'original el 2006-04-21. [Consulta: 4 setembre 2022].
18. Smith i Missen, 1991.
19. «Mathtrek Systems» (en anglès).
20. «Chemical Equilibrium with Applications» (en anglès). NASA. Arxivat de l'original el 2000-09-01. [Consulta: 4 setembre 2022].
21. Kittel i Kroemer, 1980.

Bibliografia

• Atkins, Peter; De Paula, Julio. Atkins' Physical Chemistry (en anglès). W. H. Freeman, 2006. ISBN 0-7167-8759-8. 
• Atkins, Peter W.; Jones, Loretta. Chemical Principles: The Quest for Insight (en anglès), 2008. ISBN 978-0-7167-9903-0. 
• Atkins, P.; de Paula, J.; Friedman, R. Physical Chemistry – Quanta, Matter and Change (en anglès). Freeman, 2014. 
• Beck, M. T.; Nagypál, I. Chemistry of Complex Equilibria (en anglès). Budapest: Akadémiai Kaidó, 1990. 
• Berthollet, C. L.. Essai de statique chimique (en francès). París: Firmin Didot, 1803. 
• Brady, James E. Chemistry: Matter and Its Changes (en anglès). Fred Senese, 2004. ISBN 0-471-21517-1. 
• Clugston, Michael J. «A mathematical verification of the second law of thermodynamics from the entropy of mixing» (en anglès). Journal of Chemical Education, 67(3), 1990. Bibcode: 1990JChEd..67Q.203C. DOI: 10.1021/ed067p203.
• Davies, C. W.. Ion Association (en anglès). Butterworths, 1962. 
• Kittel, C.; Kroemer, H. «9». A: Thermal Physics (en anglès). 2a edició. W. H. Freeman Company, 1980. ISBN 0-7167-1088-9. 
• Leggett, D. J.. Computational Methods for the Determination of Formation Constants (en anglès). Plenum Press, 1985. 
• Martell, A. E.; Motekaitis, R. J.. The Determination and Use of Stability Constants (en anglès). Wiley-VCH, 1992. 
• Mortimer, R. G.. Physical Chemistry (en anglès). Academic Press, 2008. 
• Rossotti, F. J. C.; Rossotti, H. The Determination of Stability Constants (en anglès). McGraw-Hill, 1961. 
• Schultz, Mary Jane «Why Equilibrium? Understanding Entropy of Mixing» (en anglès). Journal of Chemical Education, 76(10), 1999. Bibcode: 1999JChEd..76.1391S. DOI: 10.1021/ed076p1391.
• Smith, W. R.; Missen, R. W.. Chemical Reaction Equilibrium Analysis: Theory and Algorithms (en anglès). Malabar, FL: Krieger Publishing, 1991. 
• van 't Hoff, J. H.. Études de Dynamique Chemique (en francès). Amsterdam: Frederik Muller & Co., 1884. 
• Van Zeggeren, F.; Storey, S. H.. The Computation of Chemical Equilibria (en anglès). Cambridge University Press, 1970.  S'ocupa principalment dels equilibris de fase gasosa.

Vegeu també

• Acidosi
• Alcalosi
• Cinètica de Michaelis-Menten
• Constant d'equilibri
• Equació de Henderson-Hasselbalch
• Equilibri de Schlenk
• Gasometria arterial
• pCO₂
• pH
• pK_a
• Potencial normal d'elèctrode