|
আধুনিক পদাৰ্থবিজ্ঞান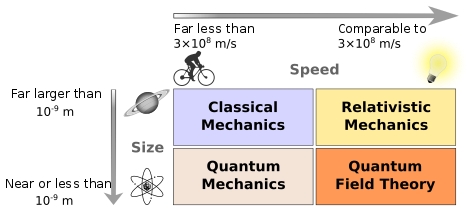 আধুনিক পদাৰ্থবিজ্ঞান বুলিলে নিউটনৰ পৰৱৰ্তী কালছোৱাত বিকশিত হোৱা পদাৰ্থবিজ্ঞানৰ ধাৰণাসমূহক বুজোৱা হয়। আচলতে ভৌতিক পৰিঘটনাসমূহক ধ্ৰুপদী তত্ত্বৰে ব্যাখ্যা আগবঢ়াবলৈ যাওঁতে কিছুমান আসোঁৱাহ ৰৈ গৈছিল। সেইবাবে প্ৰকৃতিৰ নীতি-নিয়মসমূহ সঠিকভাৱে বুজিবলৈ নিউটনৰ দিনৰ ধ্ৰুপদী তত্ত্বক অতিক্ৰম কৰি কিছুমান নতুন বিকশিত তত্ত্বৰ প্ৰয়োজন হৈছিল। প্ৰকৃতিৰ গূঢ়াৰ্থ বুজিবলৈ কোৱাণ্টাম বলবিজ্ঞান, আইনষ্টাইনৰ আপেক্ষিকতাবাদ তত্ত্ব অথবা দুয়োটাৰে আৱশ্যক হৈছিল। দৰাচলতে আধুনিক পদাৰ্থবিজ্ঞান বুলিলে কুৰি শতিকাৰ প্ৰথমভাগত জন্ম হোৱা তত্ত্ব বা ইয়াৰ প্ৰভাৱত পৰৱৰ্তী সময়ছোৱাত বিকশিত পদাৰ্থবিজ্ঞানৰ যিকোনো ক্ষেত্ৰকে বুজোৱা হয়। কম বেগ আৰু দীৰ্ঘ দূৰত্ব হৈছে ধ্ৰুপদী পদাৰ্থবিজ্ঞানৰ এক অবিচ্ছেদ্য অংগ। কিন্তু আধুনিক পদাৰ্থবিজ্ঞানে একেবাৰে চূড়ান্ত অৱস্থাবোৰহে বিশ্লেষণ কৰে। উদাহৰণস্বৰূপে কোৱাণ্টাম পৰিঘটনাসমূহ পৰমাণুৰ পৰ্যায়ৰ আকাৰতহে (প্ৰায় ১০−৯ মিটাৰ) দৃশ্যমান হয়। আনফালে আপেক্ষিকতাবাদৰ প্ৰভাৱসমূহ একেবাৰে পোহৰৰ বেগৰ পৰ্য্যায়তহে (প্ৰায় ৩ × ১০৮ মিটাৰ/ছেকেণ্ড) দৃষ্টিগোচৰ হয়। সাধাৰণতে কোৱাণ্টাম আৰু আপেক্ষিক প্ৰভাৱসমূহ যিকোনো পৰ্য্যায়ৰ স্কেলতে বিৰাজমান, কিন্তু দৈনন্দিন জীৱনত সিহঁতৰ প্ৰভাৱ প্ৰায় নগণ্য। থূলমূল আভাসআক্ষৰিক অৰ্থৰে চাবলৈ গ'লে আধুনিক পদাৰ্থবিজ্ঞান হৈছে সময়ৰ লগত খাপ খোৱা পদাৰ্থবিজ্ঞান। এইটো অৰ্থত ধ্ৰুপদী পদাৰ্থবিজ্ঞানৰ কিছু অংশও আধুনিক।[1] কিন্তু প্ৰায় ১৮৯০ চনৰ পিছৰ কালছোৱাত আৱিষ্কৃত কোৱাণ্টাম বলবিজ্ঞান, আপেক্ষিকতাবাদ আদি তত্ত্বই মানুহৰ দৃষ্টিভংগীৰ ব্যাপক পৰিৱৰ্তন ঘটাইছে।[1] সেইবাবে পদাৰ্থবিজ্ঞানৰ যিবোৰ অংশত কোৱাণ্টাম বলবিজ্ঞান বা আপেক্ষিকতাবাদৰ প্ৰভাৱ পৰিছে, সেইবোৰকহে আধুনিক পদাৰ্থবিজ্ঞানৰ আওতাত ৰখা হয়। আৰু এইটো অৰ্থতে 'আধুনিক পদাৰ্থবিজ্ঞান' শব্দটো ব্যৱহাৰ কৰা হয়। চূড়ান্ত (extreme) পৰিস্থিতিবোৰ অধ্যয়ন কৰিবলৈ আধুনিক পদাৰ্থবিজ্ঞানৰ সহায় লোৱা হয়। ক্ষুদ্ৰাতিক্ষুদ্ৰ পৰিস্থিতিবোৰৰ (নিম্ন উষ্ণতা, নিম্ন দূৰত্ব ইত্যাদি) ক্ষেত্ৰত কোৱাণ্টাম প্ৰভাৱ পৰিস্ফূত হয়, আনফালে বৃহৎ পৰিসৰৰ ক্ষেত্ৰত (অতি উচ্চ বেগ, দীৰ্ঘ দূৰত্ব ইত্যাদি) আপেক্ষিকতাবাদৰ প্ৰভাৱ দেখা যায়। এই দুই চূড়ান্ত পৰিস্থিতিৰ মাজৰ ভাগত ধ্ৰুপদী আচৰণবোৰে প্ৰভাৱ বিস্তাৰ কৰে। উদাহৰণস্বৰূপে কোঠালিৰ উষ্ণতাত গেছ এটাৰ আচৰণ অধ্যয়ন কৰিবলগীয়া হ'লে, বেছিভাগ পৰিঘটনাৰ বাবেই ধ্ৰুপদী তত্ত্ব মেক্সৱেল-ব'ল্টজমেন বিস্তাৰণৰ সহায় লোৱা হ'ব। কিন্তু পৰম শূন্য উষ্ণতাৰ ওচৰত মেক্সৱেল-ব'ল্টজমেন বিস্তাৰণে গেছৰ দৃশ্যমান আচৰণ ব্যাখ্যা কৰিব নোৱাৰে। তাৰ পৰিৱৰ্তে আধুনিক পদাৰ্থবিজ্ঞানৰ তত্ত্ব ফাৰ্মি-ডিৰাক বা ব'স-আইনষ্টাইন বিস্তাৰণহে প্ৰয়োগ কৰিবলগীয়া হয়।   বহুক্ষেত্ৰত কম বেগ আৰু দীৰ্ঘ দূৰত্বৰ বাবে আধুনিক পদাৰ্থবিজ্ঞানৰ তত্ত্বসমূহ প্ৰয়োগ কৰিও ধ্ৰুপদী পদাৰ্থবিজ্ঞানৰ ফলাফলসমূহ ঘূৰাই পাব পাৰি। ইয়াৰ ফলত লাভ কৰা ফলাফলবোৰক ধ্ৰুপদী সীমা (classical limit) বোলা হয়। 
- এফ. কে. ৰিচ্ছমায়াৰ, ই. এইচ. কেনাৰ্ড, টি. লৰিটচেন, ইণ্ট্ৰ'ডাকচন টু মডাৰ্ন ফিজিক্স, পঞ্চম সংস্কৰণ (১৯৫৫) হলমাৰ্কতলত বিষয়সমূহে আধুনিক পদাৰ্থবিজ্ঞানৰ মূল ভেটিটো গঢ় দিয়া বুলি ক'ব পাৰি।
লগতে চাওক
তথ্যসূত্ৰ
অতিৰিক্ত পঠনসামগ্ৰী
|
Portal di Ensiklopedia Dunia

