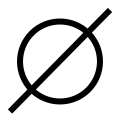
في الرياضيات ، وعلى الأخص في نظرية المجموعات ، المجموعة الخالية [ 1] الفئة الخالية [ 2] بالإنجليزية : Empty set ) هي مجموعة لا تحوي أي عنصر . أي:
M
=
∅
⇔
∀
x
:
x
∉
M
{\displaystyle M=\varnothing \Leftrightarrow \forall x:x\not \in M}
يعود أصل الرمز المستعمل من أجل الدلالة على المجموعة الفارغة إلى الحرف Ø ، المنتمي إلى الأبجدية الدنماركية والنرويجية والفاروية . ولا صلة له بالحرف الإغريقي Φ .
لكل مجموعة A :
المجموعة الفارغة هي مجموعة جزئية للمجموعة A.
اتحاد A مع المجموعة الفارغة هو A.
تقاطع A مع المجموعة الفارغة هو المجموعة الفارغة.
المجموعة الجزئية الوحيدة للمجموعة الفارغة هي المجموعة الفارغة نفسها.
الجداء الديكارتي ل A مع المجموعة الفارغة هو المجموعة الفارغة.
مجموعة التطبيقات للمجموعة الفارغة في A مفرد وعنصره الوحيد هو التطبيق الفارغ.
إذا كانت A مجموعة غير فارغة، فإن مجموعة التطبيقات ل A في المجموعة الفارغة هو المجموعة الفارغة. المجموعة الفارغة منتهية، وعدد عناصرها (card) هو 0.
Paul Halmos, Naive set theory . Princeton, NJ: D. Van Nostrand Company, 1960. Reprinted by Springer-Verlag, New York, 1974. ISBN 0-387-90092-6 (Springer-Verlag edition).
Jech, Thomas, 2003. Set Theory: The Third Millennium Edition, Revised and Expanded . Springer. ISBN 3-540-44085-2 .