|
Tegangan geser
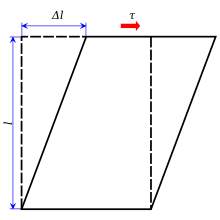 Tegangan geser (bahasa Inggris: shear stress), diberi lambang (Yunani: tau), didefinisikan sebagai komponen tegangan coplanar dengan penampang melintang sebuah benda. Tegangan geser timbul dari komponen vektor gaya paralel ke penampang melintang. tegangan normal, di sisi lain, muncul dari komponen vektor gaya tegak lurus dari penampang melintang bahan. Tegangan geser umumRumus untuk menghitung tegangan geser rata-rata adalah gaya dibagi luas:[1] di mana:
Bentuk lainmurniTegangan geser murni berhubungan dengan regangan geser murni, dilambangkan dengan , dengan persamaan berikut:[2] di mana adalah modulus geser bahan itu, yang dihitung dengan Di sini adalah modulus Young dan adalah rasio Poisson. Beam shearBeam shear didefinisikan sebagai tegangan geser internal suatu beam yang disebabkan oleh gaya geser pada beam itu. di mana
Rumus beam shear juga dikenal sebagai rumus "Zhuravskii Shear Stress" menurut Dmitrii Ivanovich Zhuravskii yang menurunkannya pada tahun 1855.[3][4] Impact shearTegangan geser maksimum yang ditimbulkan oleh subyek batangan bulat padat terhadap impak dihitung dengan persamaan: di mana
dan
Tegangan geser dalam cairanSetiap cairan (termasuk benda cair dan gas) bergerak sepanjang batasan (boundary) padat akan mengalami suatu tegangan geser pada batasan itu. Kondisi tidak selip[5] menyatakan bahwa kecepatan cairan pada suatu batasan (terhadap batasan itu) adalah nol, tetapi pada ketinggian tertentu dari batasan, kecepatan aliran harus sama dengan kecepatan cairan itu. Daerah antara kedua titik ini secara tepat dinamai lapisan batasan (boundary layer). Untuk semua cairan Newtonian dalam laminar flow tegangan geser berbanding lurus dengan laju regangan dalam cairan di mana viskositas merupakan konstanta proporsionalitas itu. Namun untuk cairan bukan-Newtonian, ini tidak berlaku karena pada cairan-cairan ini viskositas tidak konstan. Tegangan geser diberikan kepada batasan sebagai hasil kehilangan kecepatan ini. Tegangan geser, untuk suatu cairan Newtonian, pada elemen permukaan yang paralel terhadap suatu bidang datar, pada titik y, dihitung dengan: di mana
Lihat pula
Referensi
Pranala luar
|
||||||||
Portal di Ensiklopedia Dunia





















