Daftar identitas logaritma

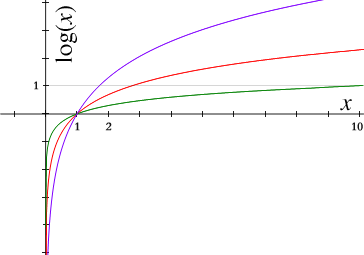
Logaritma
Domain dan Citra
Domain dari fungsi	${\displaystyle (0,\infty )}$
Daerah hasil fungsi	${\displaystyle (-\infty ,\infty )}$
Nilai-nilai spesifik
Nilai di ${\displaystyle +\infty }$	${\displaystyle \infty }$
Nilai maksimum	Tidak ada
Nilai minimum	Tidak ada
Sifat khusus
Akar	${\displaystyle 1}$
Invers	${\displaystyle x=b^{y}}$
Turunan	${\displaystyle {\frac {1}{x\ln b}}}$
Antiturunan	${\displaystyle x\log _{b}x-{\frac {x}{\ln b}}+C}$

Identitas logaritma atau dikenal sebagai hukum logaritma, ialah kumpulan rumus-rumus yang melibatkan logaritma dan bertujuan untuk mempermudah kalkulasi pada bentuk-bentuk yang cukup rumit.

Fungsi logaritma dapat didefinisikan sebagai

${\displaystyle b^{x}=c\iff \,^{b}\!\log c=x}$.

dimana ${\displaystyle b}$ adalah adalah basis atau bilangan pokok^[1] dari logaritma, dengan syarat ${\displaystyle 0<b<1}$ atau ${\displaystyle b>1}$, ${\displaystyle x}$ adalah bilangan yang dilogaritmakan yang disebut dengan numerus^[2], dan bilangan positif ${\displaystyle c}$ adalah hasil dari logaritma^[1][2] yang disebut dengan antilogaritma.^{[butuh rujukan]}

Sebagai catatan, notasi logaritma yang dipakai dalam halaman ini tetap memiliki makna yang sama dengan ${\displaystyle \log _{b}x}$, kendatipun notasinya berbeda.

Berikut adalah daftar identitas logaritma beserta dengan pembuktian-pembuktiannya, antara lain:

Salah satu yang paling mendasar dalam identitas logaritma, ialah ${\displaystyle ^{b}\!\log b=1}$, karena ${\displaystyle b^{1}=b}$. Terdapat sifat dasar lain, yaitu

• ${\displaystyle ^{b}\!\log 1=0}$, karena ${\displaystyle b^{0}=1}$.
• ${\displaystyle ^{b}\!\log b^{n}=n}$.

Sebagai pengecualian, logaritma dengan ${\displaystyle b=0}$ tidak memiliki nilai. Hasil limit dari ${\displaystyle ^{b}\!\log 0=-\infty }$ ketika ${\displaystyle b\to 0^{+}}$. Untuk memahami lebih lanjut mengenai konsep ini, lihat buktinya di sini.

• ${\displaystyle ^{b}\!\log xy=\,^{b}\!\log x+\,^{b}\!\log y}$^[3]

Sifat ini dapat diperumum ke kasus dengan numerus merupakan hasil perkalian banyak suku,

${\displaystyle ^{b}\!\log \left(\prod _{i=1}^{n}x_{i}\right)=\sum _{i=1}^{n}\,^{b}\!\log x_{i}}$.

• ${\displaystyle ^{b}\!\log \left({\frac {x}{y}}\right)=\,^{b}\!\log x-\,^{b}\!\log y}$^[3]

• ${\displaystyle ^{b}\!\log(x+y)=\,^{b}\!\log(x)+\,^{b}\!\log \left(1+{\frac {y}{x}}\right)}$
• ${\displaystyle ^{b}\!\log(x-y)=\,^{b}\!\log x+\,^{b}\!\log \left(1-{\frac {y}{x}}\right)}$

Lebih umumnya lagi,

${\displaystyle ^{b}\!\log \left(\sum _{i=0}^{n}x_{i}\right)=\,^{b}\!\log x_{0}+\,^{b}\!\log \left(1+\sum _{i=1}^{n}{\frac {a_{i}}{a_{0}}}\right)=\,^{b}\!\log x_{0}+\,^{b}\!\log \left(1+\sum _{i=1}^{n}b^{\left(^{b}\!\log x_{i}-^{b}\!\log x_{0}\right)}\right)}$.

Perubahan basis dapat dirumuskan sebagai

${\displaystyle ^{b}\!\log x={\frac {^{p}\!\log x}{^{p}\!\log b}}}$^[3]

dengan syarat ${\displaystyle 0<p<1}$ dan ${\displaystyle p>1}$ dan ${\displaystyle p\neq 1}$, dengan mengikuti definisi logaritma.^[4]

• ${\displaystyle ^{bc}\!\log x={\frac {1}{{\frac {1}{^{b}\!\log x}}+{\frac {1}{^{c}\!\log x}}}}}$
• ${\displaystyle ^{\frac {b}{c}}\!\log x={\frac {1}{{\frac {1}{^{b}\!\log x}}-{\frac {1}{^{c}\!\log x}}}}}$

Pertukaran basis pada logaritma dapat dirumuskan sebagai

${\displaystyle ^{b}\!\log x={\frac {1}{^{x}\!\log b}}}$.

• ${\displaystyle x^{\frac {\log(\log x)}{\log x}}=\log x}$ atau ${\displaystyle x^{\frac {\log a}{\log x}}=a}$

Sama halnya dengan penambahan dan pengurangan, maupun perkalian dan pembagian, logaritma dapat membatalkan eksponen karena kedua operasi tersebut saling invers. Secara matematis ini mengartikan,

${\displaystyle b^{^{b}\!\log x}=x}$ karena ${\displaystyle ^{b}\!\operatorname {antilog} (\,^{b}\!\log x)=x}$; dan

${\displaystyle ^{b}\!\log(b^{x})=x}$ karena ${\displaystyle ^{b}\!\log(\,^{b}\!\operatorname {antilog} x)=x}$.^[5]

Perhatikan bahwa sifat logaritma di atas dapat kita pakai untuk membuktikan bahwa ${\displaystyle ^{b}\!\log x^{\frac {1}{n}}={\frac {1}{n}}\,^{b}\!\log x}$.

• ${\displaystyle \lim _{x\to 0^{+}}\,^{b}\!\log x=-\infty }$
• ${\displaystyle \lim _{x\to \infty }\,^{b}\!\log x=\infty }$

Untuk membuktikan limit tersebut, perhatikan grafik fungsi logaritma basis ${\displaystyle b}$ sembarang (untuk ${\displaystyle b>1}$). Sebagai catatan, untuk ${\displaystyle 0<b<1}$,

• ${\displaystyle \lim _{x\to 0^{+}}\,^{b}\!\log x=\infty }$
• ${\displaystyle \lim _{x\to \infty }\,^{b}\!\log x=-\infty }$

Pembuktian yang serupa terhadap limit dari fungsi logaritma alami.

• ${\displaystyle \lim _{x\to 0^{+}}\ln x=-\infty }$
• ${\displaystyle \lim _{x\to \infty }\ln x=\infty }$

Sebagai tambahan, berikut adalah identitas logaritma dalam limit.

• ${\displaystyle \lim _{x\to 0^{+}}x^{c}\cdot \,^{b}\!\log x=0}$ jika ${\displaystyle c>0}$
• ${\displaystyle \lim _{x\to 0^{+}}{\frac {^{b}\!\log x}{x^{c}}}=0}$ jika ${\displaystyle c>0}$

Turunan logaritma dalam kalkulus dapat dirumuskan sebagai

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\log _{b}(x)={\frac {1}{x\ln(b)}}}$, dengan ${\displaystyle x>0}$, ${\displaystyle b>0}$, dan ${\displaystyle b\neq 1}$.

Turunan dalam basis lain, antara lain

• ${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\ln x={\frac {1}{x}}}$

Integral logaritma dalam kalkulus dapat dirumuskan sebagai

${\displaystyle \int \log _{b}(x)\,dx=x\log _{b}(x)-{\frac {x}{\ln(b)}}+C=x\left(\log _{b}(x)-{\frac {1}{\ln(b)}}\right)+C}$^[7]

Integral dalam basis lain, antara lain

• ${\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C\,}$

Sebagai catatan, halaman ini hanya menjelaskan dasar-dasarnya saja. Lihat Daftar integral dari fungsi logaritmik sebagai identitas adisionalnya.

• ${\displaystyle \ln(1+x)=\sum _{n\geq 1}{\frac {(-1)^{n-1}x^{n}}{n}}}$

• ${\displaystyle \log x\approx {\frac {x^{x}-1}{x}}}$^[8]
• ${\displaystyle \log(1+x)\approx x}$^[8]

• ${\displaystyle \ln(1+x)={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}}$

• ${\displaystyle \ln \left(1+{\frac {x}{y}}\right)={\cfrac {x}{y+{\cfrac {1x}{2+{\cfrac {1x}{3y+{\cfrac {2x}{2+{\cfrac {2x}{5y+{\cfrac {3x}{2+\ddots }}}}}}}}}}}}={\cfrac {2x}{2y+x-{\cfrac {(1x)^{2}}{3(2y+x)-{\cfrac {(2x)^{2}}{5(2y+x)-{\cfrac {(3x)^{2}}{7(2y+x)-\ddots }}}}}}}}}$

• Daftar identitas eksponensiasi

1. ^ ^{a b} Archangelia Maria Lelu, Desain Pembelajaran Pada Materi Fungsi Logaritma Menggunakan Pendekatan Pembelajaran Berbasis Masalah dan Hasil Pembelajaran Ditinjau dari Kemampuan Komunikasi Matematis Siswa Kelas X MIPA Diarsipkan 2021-10-22 di Wayback Machine., hlm. 15.
2. ^ ^{a b} Entis Sutisna, S.Pd, Fungsi Eksponen dan Fungsi Logaritma Matematika Peminatan Kelas X Diarsipkan 2021-10-21 di Wayback Machine., hlm. 29.
3. ^ ^{a b c d} Kanginan, Marthen; Nurdiansyah, Hadi; Akhmad, Ghany (2016). Matematika Untuk Siswa SMA/MA Kelas X. Yrama Widya. hlm. 74. ISBN 978-602-374-554-8.  Parameter |url-status= yang tidak diketahui akan diabaikan (bantuan)
4. ^ Referensinya (pada bagian definisi) mencakup di sini.
5. ^ "Antilogarithm". Wolfram MathWorld. 
6. ^ Dale Varberg, Edward Purcell, Steve Rigdon (2006). Kalkulus Edisi Kesembilan, Jilid 1. hlm. 336. (Penerjemah: I Nyoman Susila, Ph. D, Penerbit Erlangga)
7. ^ "Logarithm Rules". RapidTables. 
8. ^ ^{a b} "approximation of the log function". planetmath.org. Diakses tanggal 2013-03-22 15:18:38.  Parameter |first1= tanpa |last1= di Authors list (bantuan); Periksa nilai tanggal di: |access-date= (bantuan)