|
Konstanta (matematika)Dalam matematika, konstanta atau tetapan adalah suatu nilai tetap berlawanan dengan variabel yang berubah-ubah. Konstanta digunakan dalam berbagai disiplin ilmu, seperti fisika, geometri dan muncul dalam berbagai bentuk matematika lainnya. Fungsi konstan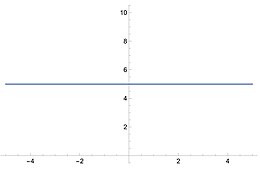 Sebuah konstan dapat dipakai untuk menyatakan sebuah fungsi konstan, sebuah fungsi yang mengabaikan argumen (nilai masukan)-nya dan selalu memberikan hasil nilai yang sama.[1] Misalkan, diketahui ada sebuah fungsi konstan dengan satu variabel, katakanlah . Fungsi ini mempunyai grafik yang memuat sebuah garis horizontal yang sejajar dengan sumbu-x.[2] Fungsi tersebut selalu memberikan nilai yang sama, yaitu 5, karena tidak ada variabel yang memuat di dalam bentuk fungsi tersebut. Ketergantungan konteksSifat konsep "konstanta" yang bergantung pada konteks dapat dilihat dalam contoh dari kalkulus dasar: "Konstanta" berarti tidak bergantung pada setiap variabel dan tidak berubah saat variabel berubah. Pada kasus pertama di atas, konstanta x berarti tidak bergantung pada h, sedangkan pada kasus kedua di atas, konstanta berarti tidak bergantung pada x. Dalam konteks yang lebih sempit, konstanta dapat dipandang sebagai variabel dalam konteks yang lebih luas. Konstanta matematika pentingAda beberapa nilai yang sering muncul dalam matematika dan secara konvensional dilambangkan dengan simbol tertentu. Simbol standar dan nilainya disebut konstanta matematika. Sebagai contoh:
Konstanta dalam kalkulusDalam kalkulus, konstanta diperlakukan dalam beberapa cara berbeda tergantung operasinya. Sebagai contoh, turunan dari fungsi konstanta adalah nol. Menurut definisi, hal ini dikarenakan konstanta tidak berubah. Jadi, turunannya adalah nol. Sebaliknya, jika mengintegrasikan sebuah fungsi konstanta, konstanta tersebut dikalikan dengan variabel integrasi. Ketika menghitung suatu limit, konstanta tetap sama seperti sebelum dan sesudah perhitungan. Integrasi fungsi dari satu variabel seringkali melibatkan konstanta integral. Konstanta tersebut muncul karena bahwa operator integral merupakan invers dari operator diferensial. Artinya, tujuan integrasi adalah untuk memulihkan fungsi asli sebelum diferensiasi. Seperti yang dijelaskan contoh di atas, turunan dari fungsi konstanta adalah nol dan operator diferensial adalah operator linear, sehingga fungsi yang hanya berbeda dengan suku konstanta memiliki turunan yang sama. Untuk membenarkannya dan memastikan bahwa semua solusi yang mungkin disertakan, konstanta integrasi ditambahkan ke integral taktentu. Biasanya, konstanta integrasi ditulis sebagai , dan mewakili konstanta dengan nilai tetap, namun nilainya belum ditentukan. Lihat pulaReferensi
Pranala luar
|
Portal di Ensiklopedia Dunia

![{\displaystyle {\begin{aligned}{\frac {d}{dx}}2^{x}&=\lim _{h\to 0}{\frac {2^{x+h}-2^{x}}{h}}=\lim _{h\to 0}2^{x}{\frac {2^{h}-1}{h}}\\[8pt]&=2^{x}\lim _{h\to 0}{\frac {2^{h}-1}{h}}&&{\text{karena }}x{\text{ konstanta (tidak bergantung pada }}h{\text{)}}\\[8pt]&=2^{x}\cdot \mathbf {konstanta,} &&{\text{dengan }}\mathbf {konstanta} {\text{ berarti tidak bergantung pada }}x.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4551104afed1a8341d32332dde2bcd3678e7685a)


