|
0,999...0,999… dalam matematika adalah suatu bilangan desimal yang memuat angka 9 berulang tak terhingga. Juga bisa ditulis sebagai , , atau . Bilangan ini merupakan sebuah bilangan real yang secara matematis memiliki nilai sama dengan 1. Dengan kata lain, "0,999…" mewakili bilangan yang sama dengan angka "1". Persamaan ini telah lama diterima oleh para matematikawan dan diajarkan di buku-buku teks pelajaran. Beberapa pembuktian matematis mengenai identitas ini telah dirumuskan. Ketidaktunggalan ekspansi bilangan real 0,999… tidaklah terbatas hanya pada sistem bilangan desimal. Fenomena yang sama juga terjadi pada semua sistem berbilangan pokok bulat, dan para matematikawan juga telah mengkuantifikasi cara penulisan 1 ke dalam representasi takbulat. Fenomena ini juga tidak hanya terjadi pada 1: setiap bilangan desimal berakhir bukan nol, memiliki kembaran dengan angka 9 tak terhingga, misalnya 28,3287 adalah sama dengan 28,32869999…. Atas alasan kesederhanaan, bilangan desimal berakhir tersebut hampir selalu dipilih, yang pada akhirnya terjadi miskonsepsi bahwa ia adalah satu-satunya representasi bilangan tersebut. Bahkan lebih luas lagi, sistem bilangan posisional apapun mengandung sejumlah tak terhingga bilangan dengan representasi berganda. Berbagai identitas ini telah diterapkan untuk membantu memahami pola ekspansi desimal pecahan dan struktur fraktal sederhana seperti himpunan Cantor. Pada beberapa dekade ini, para peneliti pendidikan matematika telah melakukan kajian sejauh mana tingkat penerimaan para siswa dalam menerima persamaan ini. Walaupun telah diyakinkan oleh buku teks, guru pengajar, dan penjelasan aritmetika mengenai persamaan ini, para siswa tetap merasa tidak yakin dan melakukan pembenaran lebih lanjut untuk menolak persamaan ini. Alasan penolakan para siswa biasanya didasarkan pada miskonsepsi umum mengenai bilangan real; yakni setiap bilangan real mempunyai ekspansi desimal yang tunggal, bahwa bilangan real kecil tak terhingga haruslah ada, ataupun ekspansi 0,999… pada akhirnya akan berakhir. Sistem bilangan yang menghapuskan intuisi yang salah ini dapat dibangun, tetapi hanya dapat dibangun di luar sistem bilangan real standar yang digunakan dalam matematika dasar. Pengantar0,999… adalah sebuah bilangan yang ditulis dengan menggunakan sistem bilangan desimal. Beberapa pembuktian sederhana 0,999… = 1 bergantung pada kemudahan sifat-sifat aritmetika sistem ini. Kebanyakan aritmetika desimal (penjumlahan, pengurangan, perkalian, pembagian, dan perbandingan) menggunakan manipulasi pada tingkat digit, yang mirip pada bilangan bulat. Pada bilangan bulat, dua desimal terhingga apapun dengan digit berbeda adalah dua bilangan yang berbeda. Secara khusus, bilangan apapun dalam bentuk 0,99…9, dengan angka 9 yang pada akhirnya berakhir adalah lebih kecil dari 1. Penafsiran yang salah terhadap arti penggunaan "…" (elipsis) pada 0,999… bertanggung jawab atas miskonspesi mengenai persamaannya dengan 1. Penggunaannya dalam hal ini berbeda dengan penggunaannya dalam bahasa maupun dalam 0,99…9, yang mana elipsis mengalamatkan bagian terhingga yang tidak dinyatakan ataupun diabaikan. Ketika digunakan dalam desimal berulang, "…" berarti bagian tak terhingga yang tidak disebutkan, dan hanya bisa diinterpretasikan sebagai sebuah bilangan menggunakan konsep matematika limit. Sehingga, dalam penggunaan matematika konvensional, nilai yang diberikan untuk notasi "0.999…" adalah bilangan real dengan limit deret konvergen (0,9, 0,99, 0,999, 0,9999, …). Tidak seperti pada kasus bilangan bulat dan desimal terhingga, notasi bilangan lainnya dapat mengekspresikan sebuah bilangan dengan banyak cara. Sebagai contoh penggunaan pecahan 1/3 = 2/6. Desimal tak terhingga, dapat mengekspresikan bilangan yang sama dengan paling banyak dua cara, yakni dengan deret sembilan berulang tak terhingga, dan dengan deret nol berulang tak terhingga (biasanya diabaikan penulisannya). Terdapat banyak pembuktian dalam berbagai tingkat kecermatan matematika yang membuktikan 0,999… = 1. Salah satu pembuktian cermat itu dapat dinyatakan secara singkat sebagai berikut: dua bilangan real adalah identik jika dan hanya jika perbedaan dua bilangan tersebut adalah nol. Kebanyakan orang akan menyetujui bahwa perbedaan antara 0,999… dengan 1, jika ada, adalah sangat kecil. Dengan mempertimbangkan barisan konvergen di atas, kita dapat menunjukkan bahwa besaran perbedaan ini haruslah lebih kecil dari kuantitas positif apapun, dan dapat ditunjukkan bahwa bilangan real satu-satunya yang memenuhi sifat ini adalah 0. Oleh karena perbedaannya adalah 0, disimpulkan bahwa bilangan 1 dan 0,999… adalah identik. Argumen yang sama juga menjelaskan mengapa 0,333… = 1/3, 0,111… = 1/9, dst. PembuktianAljabarPecahanSalah satu alasan mengapa desimal tak terhingga merupakan perluasan yang perlu dari desimal terhingga adalah untuk merepresentasikan pecahan. Dengan menggunakan pembagian panjang, pembagian bilangan bulat yang sederhana seperti 1⁄3 akan menghasilkan desimal berulang 0,333…. Desimal berulang ini mempunyai digit yang berulang tanpa akhir. Desimal ini memberikan bukti cepat 0,999… = 1. Perkalian 3 kali 3 menghasilkan 9 pada setiap digit, sehingga 3 × 0,333… sama dengan 0,999…. Dan 3 × 1⁄3 sama dengan 1, sehingga 0,999… = 1.[1] Bentuk pembuktian lainya adalah perkalian 1/9 = 0.111… dengan 9. Versi pembuktian yang sama yang lebih mudah dimengerti adalah berdasarkan persamaan berikut: Oleh karena kedua persamaan berlaku berdasarkan sifat transitif, 0,999… haruslah sama dengan 1. Hal yang sama, 3/3 = 1, dan 3/3 = 0,999…. Sehingga, 0.999… haruslah sama dengan 1. Manipulasi digitBentuk pembuktian lainnya menggunakan desimal berulang lainnya. Ketika sebuah bilangan dalam notasi desimal dikalikan dengan 10, digit itu tidak akan berubah, tetapi pemisah desimal akan berpindah satu digit ke kanan. Sehingga 10 x 0,999… sama dengan 9.999…. Pengurangan 0,999… dari 9,999… dapat dilakukan secara digit per digit; di setiap digit setelah pemisah desimal, hasil 9-9 adalah 0. Namun nol yang berulang-ulang ini tidak akan mengubah sebuah bilangan, sehingga perbedaannya adalah persis 9. Langkah akhirnya kemudian menggunakan aljabar. Misalnya bilangan desimal yang dipertanyakan (0.999…) disebut x. Maka 10x − x = 9. Ini adalah sama dengan 9x = 9. Pembagian kedua sisi oleh 9 menyelesaikan pembuktian: x = 1.[1] Validitas manipulasi digit pada bukti di atas tidak perlu dianggap sebagai sebuah aksioma; ia mengikuti hubungan dasar antara desimal dengan bilangan yang ia representasikan. Hubungan ini, yang dapat dikembangkan menjadi beberapa cara yang setara, telah membentuk hubungan desimal 0,999… dan 1,000... mewakili bilangan yang sama. AnalitikOleh karena permasalahan 0,999… tidak memengaruhi perkembangan formal matematika, permasalahan ini dapat ditunda sementara sampai kita dapat membuktikan teorema standar analisis real. Satu persyaratannya adalah mengkarakterisasikan bilangan real yang dapat ditulis ke dalam notasi desimal: terdiri dari tanda pilihan, barisan terhingga bilangan apapun dari digit yang membentuk bagian bilangan bulat, pemisah desimal, dan barisan digit yang membentuk bagian pecahan. Untuk tujuan diskusi 0,999…, bagian bilangan bulat dapat diringkas sebagai b0 dan dapat mengabaikan bilangan negatif, sehingga sebuah ekspansi desimal mempunyai bentuk: Adalah penting bahwa bagian pecahan, tidak seperti pada bagian bilangan bulat, tidaklah terbatas pada jumlah digit yang terhingga. Deret dan barisan tak terhinggaMetode ekspansi desimal yang paling umum digunakan adalah dengan mendefinisikannya sebagai penjumlahan deret tak terhingga. Secara umum: Untuk 0,999…, kita dapat menggunakan teorema konvergen deret geometri:[2]
Oleh karena 0,999… adalah penjumlahan dengan rasio umum : Pembuktian ini (sebenarnya 10 sama dengan 9,999…) muncul pada tahun 1770 pada buku "Vollständige Anleitung zur Algebra" (Bahasa Indonesia: Instruksi lengkap Aljabar) Leonhard Euler.[3] 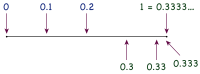 Hasil penjumlahan deret geometri itu sendiri telah ada sebelum Euler. Penjabaran abad-18 yang umumnya dilakukan adalah dengan menggunakan manipulasi suku per suku yang mirip dengan pembuktian aljabar di atas. Pada akhir tahun 1811, pada buku teks Bonnycastle An Introduction to Algebra, ia menggunakan argumen deret geometri untuk membenarkan pembuktian 0,999… tersebut.[4] Reaksi abad 19 yang menentang metode penjumlahan liberal tersebut memunculkan definisi penjumlahan yang sampai sekarang masih mendominasi, yakni: penjumlahan sebuah deret didefinisikan sebagai limit barisan dari jumlah parsialnya. Pembuktian teorema ini secara eksplisit menghitung barisan tersebut.[5] Sebuah barisan (x0, x1, x2, …) mempunyai limit x jika jarak |x − xn| menjadi sangat kecil ketika n bertambah. Penyataan 0,999… = 1 itu sendiri dapat diinterpretasikan dan dibuktikan sebagai limit: Pada bagian terakhir,——dibenarkan oleh aksioma yang menyatakan bahwa bilangan real mempunyai sifat Archimedes. Pandangan terhadap 0,999… yang berdasarkan limit ini mungkin akan lebih mudah diingat, tetapi kuranglah tepat. Sebagai contoh, buku teks The University Arithmetic tahun 1846 menjelaskan, ",999 + berlanjut sampai tak terhingga = 1 karena setiap aneksasi 9 membawa nilai itu semakin dekat dengan 1"; buku Arithmetic for Schools tahun 1895 mengatakan, "…ketika sejumlah bilangan 9 yang sangat banyak dibawa, perbedaan antara 1 dan,99999… akan menjadi tidak bisa dibayangkan kecilnya".[7] Heuristik seperti ini sering diinterpretasikan oleh para siswa mengimplikasikan 0,999… itu sendiri lebih kecil daripada 1. Interval bersarang dan batas atas terkecil Definisi deret di atas merupakan salah satu cara yang mudah untuk mendefinisikan bilangan real yang berasal dari ekspansi desimal. Pendekatan komplementer lainnya menggunakan proses yang berlawanan, yaitu untuk sebuah bilangan real yang diberikan, definisikan ekspansi desimalnya. Jika diketahui sebuah bilangan real x berada dalam interval tertutup [0, 10] (yakni lebih besar atau sama dengan 0 dan lebih kecil atau sama dengan 10), seseorang dapat membagi interval tersebut menjadi 10 interval yang bertumpang tindih hanya pada titik akhirnya: [0, 1], [1, 2], [2, 3],dan seterusnya sampai [9, 10]. Bilangan x haruslah berada dalam salah satu interval ini; jika ia ada dalam [2, 3], maka simpan digit "2" dan bagi interval tersebut menjadi [2, 2,1], [2,1, 2,2], …, [2,8, 2,9], [2,9, 3]. Kelanjutan proses ini akan menghasilkan barisan tak terhingga interval bersarang, yang ditandai oleh barisan tak terhingga digit-digit b0, b1, b2, b3, …, dan dapat ditulis
Pada formalisme ini, identitas 1 = 0,999… dan 1 = 1,000… merefleksikan fakta bahwa 1 berada di baik interval [0, 1] maupun [1, 2], sehingga seseorang dapat memilih salah satu subinterval tersebut untuk menemukan digitnya. Untuk memastikan notasi ini tidak menyalahgunakan tanda "=", seseorang perlulah menemukan cara untuk merekonstruksi sebuah bilangan real tunggal untuk setiap desimal. Hal ini dapat dilakukukan dengan menggunakan limit, tetapi terdapat pula cara-cara lainnya.[8] Salah satu pilihan yang tepat sasaran adalah teorema interval bersarang, yang memastikan bahwa untuk sebuah barisan tersarang dengan interval tertutup yang panjangnya menjadi sangat kecil, interval-intervalnya akan mengandung persis satu bilangan real pada perpotongannya. Sehingga b0,b1b2b3… didefinisikan menjadi bilangan tunggal yang terkandung dalam semua interval [b0, b0 + 1], [b0,b1, b0,b1 + 0,1], dan seterusnya. Maka 0,999… adalah bilangan real tunggal yang berada pada semua interval [0, 1], [0,9, 1], [0,99, 1], dan [0,99…9, 1] untuk setiap untaian 9 yang terhingga. Oleh karena 1 merupakan elemen pada setiap interval ini, 0,999… = 1.[9] Teorema interval bersarang ini biasanya bertumpu pada karakteristik dasar bilangan real, yaitu keberadaan batas atas terkecil atau suprema. Untuk secara langsung menggunakan karakteristik ini, seseorang dapat mendefinisikan b0,b1b2b3… sebagai batas atas himpunan hampiran {b0, b0,b1, b0,b1b2, …}.[10] Kita kemudian dapat menunjukkan bahwa definisi ini (atau definisi interval bersarang) konsisten dengan prosedur subdivisi, mengimplikasikan 0,999… = 1. Tom Apostol berkesimpulan,
Berdasarkan konstruksi bilangan realBeberapa pendekatan secara eksplisit mendefinisikan bilangan real sebagai struktur tertentu yang dibangun dari bilangan rasional menggunakan teori himpunan aksiomatik. Bilangan asli—0, 1, 2, 3, dan seterusnya—dimulai dari 0 dan berlanjut ke atas, sehingga setiap bilangan mempunyai penerusnya. Kita dapat memperluas bilangan asli dengan nilai negatifnya, sehingga didapatkan bilangan bulat, lebih jauh lagi bisa diperluas menjadi pecahan, sehingga didapatkanlah bilangan rasional. Sistem bilangan ini diikuti oleh aritmetika penjumlahan, pengurangan, perkalian, dan pembagian. Lebih rinci lagi, sistem ini melibatkan pengurutan, sehingga bilangan yang satu dapat dibandingkan dengan bilangan yang lain, sehingga terdapat hubungan lebih kecil, sama dengan, dan lebih besar. Langkah perluasan bilangan rasional menjadi bilangan real adalah perluasan yang sangat besar. Terdapat paling sedikit dua cara untuk melakukannya. Kedua cara ini dipublikasikan pada tahun 1872, yakni potongan Dedekind dan barisan Cauchy. Pembuktian 0,999… = 1 yang secara langsung menggunakan konstruksi ini dapat ditemukan dalam buku-buku teks analisis real. Potongan DedekindDalam pendekatan potongan Dedekind, setiap bilangan real x didefinisikan sebagai himpunan takhingga dari semua bilangan rasional yang lebih kecil daripada x.[12] Secara spesifik, bilangan real 1 adalah himpunan semua bilangan rasional yang lebih kecil dari 1.[13] Setiap ekspansi desimal positif dapat dengan mudah menentukan potongan Dedekind, yakni himpunan bilangan rasional yang lebih kecil dari beberapa tahap ekspansi. Sehingga bilangan real 0,999… adalah himpunan bilangan rasional r sedemikian rupanya r < 0, atau r < 0,9, atau r < 0,99, atau r lebih kecil dari bilangan lainnya yang berbentuk .[14] Setiap unsur 0,999… adalah lebih kecil dari 1, sehingga ia adalah unsur dari bilangan real 1. Kebalikannya, bilangan 1 adalah bilangan rasional , yang mengimplikasikan . OLeh karena 0,999… dan 1 mengandung bilangan rasional yang sama, 0,999… dan 1 adalah himpunan yang sama, sehingga 0,999… = 1. Definisi bilangan real sebagai potongan Dedekind pertama kali dipublikasikan oleh Richard Dedekind pada tahun 1872.[15] Pendekatan seperti di atas dengan penunjukkan sebuah bilangan ke setiap ekspansi desimalnya pertama kali terdapat dalam naskah yang berjudul "Is 0.999 … = 1?" oleh Fred Richman pada majalah Mathematics Magazine yang ditujukan ke para pengajar matematika tingkat perguruan tinggi, terutama tingkat junior/senior, dan murid-muridnya.[16] Richman menemukan bahwa dengan mengambil potongan Dedekind pada subhimpunan rapat bilangan rasional apapun akan menghasilkan hasil yang sama; khususnya, dia menggunakan pecahan desimal, di mana pembuktiannya dapat langsung terlihat: "Maka kita melihat bahwa dalam definisi tradisional bilangan real, persamaan 0.9* = 1 dari awalnya sudah dibangun."[17] Barisan CauchyPendekatan konstruksi bilangan real lainnya adalah dengan menggunakan pengurutan bilangan rasional secara tidak langsung. Pertama-tama, jarak antara x dan y didefinisikan sebagai nilai mutlak |x − y| dengan nilai mutlak |z| didefinisikan sebagai nilai terbesar z dan −z, sehingga ia tidak pernah negatif. Sehingga bilangan real didefinisikan sebagai barisan bilangan rasional yang mempunyasi sifat barisan Cauchy dengan menggunakan jarak ini, yakni barisan (x0, x1, x2, …). Dalam barisan (x0, x1, x2, …) yang merupakan pemetaan bilangan asli ke bilangan rasional ini, untuk bilangan rasional positif δ apapun terdapat N sedemikian rupanya |xm − xn| ≤ δ untuk semua m, n > N. (Jarak antara setiap suku menjadi lebih kecil dari bilangan rasional positif apapun.)[18] Jika (xn) dan (yn) adalah dua barisan Cauchy, keduanya didefinisikan sebagai bilangan real yang sama jika barisan (xn − yn) mempunyai limit 0. Pemenggalan bilangan desimal b0.b1b2b3… menghasilkan sebuah barisan bilangan rasional Cauchy; ini digunakan untuk mendefinisikan nilai real dari bilangan.[19] Sehingga dalam formalisme ini, tugas kita adalah menunjukkan bahwa barisan bilangan rasional mempunyai limit 0. Untuk n=0,1,2,… kita dapat tunjukkan bahwa pada suku ke-n Limit ini dapat dengan mudah dimengerti;[20] satu pembuktian yang memungkinkan adalah dalam definisi limit barisan, untuk ε = a/b > 0 kita dapat mengambil N = b. Sehingga 0,999… = 1. Definisi bilangan rasional sebagai barisan Cauchy pertama kali dipublikasi secara terpisah oleh Eduard Heine dan Georg Cantor pada tahun 1872.[15] GeneralisasiHasil 0,999… = 1 dapat digeneralisasi ke dalam dua cara. Pertama-tama, setiap bilangan bukan nol dengan notasi desimal terhingga (atau dengan kata lain akhiran 0 takhingga) memiliki kembaran dengan akhiran 9 tak terhingga. Sebagai contoh, 0,24999… persis sama dengan 0,25. Bilangan-bilangan ini merupakan persis pecahan desimal yang sama dan bilangan-bilangan ini rapat.[21] Kedua, teorema yang terbandingkan dapat diterapkan pada setiap bilangan pokok (basis). Sebagai contoh, dalam basis 2 (sistem bilangan biner), 0,111… sama dengan 1, dan dalam basis 3 (sistem bilangan terner) 0,222… sama dengan 1. Buku-buku teks analisis real biasanya akan mengabaikan contoh 0,999… dan sebaliknya memberikan contoh-contoh generalisasi ini dari awalnya.[22] Representasi alternatif 1 juga terjadi pada sistem bilangan berbasis non-integer. Sebagai contoh, dalam basis nisbah keemasan, dua representasi standarnya adalah 1,000… dan 0,101010…. Secara umum, untuk hampir semua q antara 1 dan 2, terdapat banyak ekspansi basis-q 1 yang tak terhitung banyaknya. Di sisi lain, terdapat tak terhingga banyaknya q (termasuk pula semua bilangan asli lebih dari 1) yang mana hanya terdapat satu ekspansi 1 basis-q selain 1.000…. Hasil ini pertama kali didapatkan oleh Paul Erdős, Miklos Horváth, dan István Joó sekitar tahun 1990. Pada tahun 1998 Vilmos Komornik dan Paola Loreti berhasil menentukan basis terkecil yang memungkinkan, yakin tetapan Komornik-Loreti q = 1,787231650…. Dalam basis ini, 1 = 0,11010011001011010010110011010011…; digit ini didapatkan dari barisan Thue-Morse yang tidak berulang.[23] Generalisasi yang paling jauh mengalamatkan sistem bilangan posisional yang paling umum. Sistem-sistem ini juga mempunyai banyak representasi. Sebagai contoh:[24]
Marko Petkovšek telah membuktikan bahwa ambiguitas ini merupakan konsekuensi yang perlu dalam penggunaan sistem posisional: untuk sistem penamaan semua bilangan real apapun, himpunan bilangan real dengan representasi berganda selalu rapat.[25] AplikasiSatu aplikasi 0,999… sebagai representasi 1 dapat terlihat pada teori bilangan dasar. Pada tahun 1802, H. Goodwin mempublikasikan sebuah pengamatan kemunculan 9 dalam representasi desimal berulang pecahan yang penyebutnya merupakan bilangan prima tertentu. Sebagai contoh:
E. Midy membuktikan hasil umum dari pecahan tersebut tahun 1836, dan sekarang disebut sebagai teorema Midy. Publikasi awalnya tidak ditulis dengan jelas, dan tidakklah jelas apakah pembuktiannya melibatkan 0,999…, tetapi paling tidak pembuktian modern W. G. Leavitt ada melibatkannya. Jika seseorang dapat membuktikan sebuah bilangan desimal dalam bentuk 0,b1b2b3… adalah sebuah bilangan bulat positif, maka itu haruslah 0,999…, yang merupakan sumber 9 dalam teorema itu.[26] Investigasi lebih lanjut dengan arah seperti ini dapat menghasilkan konsep pembagi persekutuan terbesar, aritmetik modular, bilangan prima Fermat, dan timbal balik kuadratik.[27]  Kembali ke analisis real, analog basis 3 0,222… = 1 memainkan peran penting dalam karakterisasi himpunan Cantor:
Digit ke-n representasi tersebut mencerminkan posisi titik tersebut pada tahap ke-n konstruksi. Sebagai contoh, titik ²⁄3 mempunyai representasi 0,2 atau 0,2000…, karena ia terletak di sebelah kanan penghapusan pertama dan di sebelah kiri pada setiap penghapusan selanjutnya. Titik 1⁄3 direpresentasikan tidak sebagai 0,1, tetapi sebagai 0,0222…, karena ia berada di sebelah kiri penghapusan pertama dan di sebelah kanan pada setiap penghapusan selanjutnya.[28] Sembilan berulang juga terdapat dalam hasil kerja Georg Cantor lainnya. Sembilan berulang ini harus dilibatkan dalam konstruksi pembuktian absah ketaktercacahan interval satuan dengan menerapkan argumen diagonal Cantor ke ekspansi desimal. Pembuktian seperti ini perlulah dapat menentukan pasangan bilangan real tertentu sebagai bilangan yang berbeda berdasarkan ekspansi desimalnya. Sehingga kita perlu menghindari pasangan seperti 0,2 dan 0,1999….[29] Varian yang mungkin lebih dekat dengan argumen Cantor awal sebenarnya menggunakan basis 2, dan dengan mengubah ekspansi basis 3 menjadi ekspansi basis 2, seseorang juga dapat membuktikan ketaktercacahan himpunan Cantor.[30] Skeptisisme dalam pendidikanPara siswa matematika sering menolak persamaan 0,999… dengan 1 oleh karena berbagai alasan, mulai dari penampilan kedua angka yang berbeda sampai dengan ketidakpercayaan terhadap konsep limit dan ketidaksetujuan terhadap sifat-sifat infinitesimal. Terdapat banyak faktor yang berkontribusi pada kebingungan ini:
Pemikiran-pemikiran ini merupakan pemikiran yang salah dalam konteks bilangan real standar, walaupun mungkin beberapa pemikiran ini absah dalam sistem bilangan yang lainnya. Kebanyakan penjelasan-penjelasan ini ditemukan oleh Profesor David Tall yang mempelajari karakteristik pengajaran dan pengenalan yang menyebabkan beberapa kesalahpahaman yang dia temui pada murid-murid universitasnya. Setelah menanyai murid-muridnya untuk mengetahui mengapa mayoritas besar pada awalnya menolak persamaan ini, ia menemukan bahwa "siswa terus membayangkan 0,999… sebagai sebuah barisan bilangan yang semakin mendekati 1 dan bukanlah nilai yang pasti, karena 'anda belum menentukan seberapa banyak tempat desimal yang ada' atau 'ia merupakan bilangan desimal yang memungkinkan yang paling dekat dengan 1'".[34] Dengan pembuktian dasar perkalian 0,333… = 1⁄3 dengan 3 sepertinya merupakan stategi yang sukses dalam meyakinkan siswa yang ragu-ragu bahwa 0,999… = 1. Namun, ketika dihadapkan dengan konflik antara kepercayaan mereka terhadap persamaan pertama dan ketidakpercayaan terhadap persamaan kedua, beberapa siswa mulai tidak mempercayai persamaan pertama atau menjadi frustasi.[35] Metode yang lebih canggih dan rumit juga tidak membantu, siswa yang secara penuh dapat menerapkan definisi cermat masih mungkin terperangkap ke dalam intuisi mereka ketika dikejutkan oleh hasil pembuktian matematika lanjutan. Sebagai contoh, seorang siswa analisis real mampu membuktikan 0,333… = 1⁄3 menggunakan definisi supremum, tetapi tetap bersikeras bahwa 0,999… < 1 didasari oleh pemahaman pembagian panjangnya.[36] Yang lainnya dapat membuktikan 1⁄3 = 0,333…, tetapi ketika disodorkan pembuktian pecahan, mereka bersikeras bahwa "logika" melebihi perhitungan matematika. Joseph Mazur menceritakan sebuah kisah mengenai murid kalkulusnya yang brilian, yang "menantang hampir semua apa yang saya katakan di kelas namun tidak pernah mempertanyakan kalkulatornya," dan yang percaya bahwa sembilan digit adalah semua yang diperlukan dalam matematika, termasuk perhitungan akar kuadrat dari 23. Siswa tersebut terganggu dengan argumen bahwa 9,99… = 10, mengatainya sebagai "proses pertumbuhan tak terhingga yang tidak bisa dibayangkan."[37] Dalam kebudayaan populerDengan berkembangnya internet, debat mengenai 0,999… telah keluar dari ruangan kelas dan merupakan hal yang umum terlihat dalam newsgroup dan forum internet, termasuk pula banyak yang sebenarnya tidak berhubungan dengan matematika. Dalam newsgroup Kolom surat kabar The Straight Dope edisi 2003 mendiskusikan 0,999… via 1⁄3 dan limit, dan mengenai miskonspesi ini berkata,
Permasalahan 0,999… juga tampaknya merupakan topik yang populer dalam tujuh tahun pertama forum Battle.net Blizzard Entertainment, sehingga perusahaan tersebut mengeluarkan sebuah "siaran pers" pada April Mop tahun 2004 bahwa 0,999… adalah 1:
Dua pembuktian kemudian diberikan, didasarkan pada limit dan perkalian dengan 10. Sistem bilangan alternatifWalaupun sistem bilangan real membentuk sebuah sistem bilangan yang sangat berguna, keputusan untuk menginterpretasikan frasa "0,999…" sebagai penamaan sebuah bilangan real pada akhirnya merupakan sebuah konvensi, dan Timothy Gowers berargumen dalam Mathematics: A Very Short Introduction bahwa identitas 0,999… = 1 itu sendiri juga merupakan sebuah konvensi:
Seseorang dapat menentukan sistem bilangan lainnya yang menggunakan aturan yang berbeda; dalam sistem bilangan seperti ini, pembuktian di atas perlu diinterpretasi ulang, dan seseorang mungkin akan menemukan bahwa, dalam sistem bilangan ini, 0,999… dan 1 bisa tidak identik. Namun, kebanyakan sistem bilangan merupakan perluasan dari sistem bilangan real, dan bukannya sistem bilangan alternatif yang berdiri sendiri, sehingga 0,999… = 1 tetap berlaku. Walaupun begitu, adalah penting untuk mengkaji sistem bilangan alternatif, bukan hanya bagaimana kelakuan 0,999…, tetapi juga kelakukan fenomena-fenomena terkait. Jika fenomena tersebut berbeda dari yang ada dalam sistem bilangan real, maka paling tidak satu asumsi yang dibangun ke dalam sistem itu haruslah telah patah/runtuh. Kecil tak terhinggaBeberapa pembuktian 0,999… = 1 bergantung pada sifat-sifat Archimedes bilangan real standar, yakni tidaklah ada bilangan kecil tak hingga (infinitesimal) bukan nol. Terdapat struktur aljabar yang tidak mengikuti sifat Archimedes, meliputi berbagai alternatif real standar. Arti 0,999… bergantung pada struktur mana yang kita gunakan. Sebagai contoh, bilangan dual memasukkan sebuah unsur kecil tak terhingga baru ε, yang beranalogi dengan satuan imajiner i dalam bilangan kompleks, kecuali bahwa ε² = 0. Struktur ini sangat berguna dalam diferensiasi automatik. Bilangan dual dapat diberikan urutan leksikografis, sehingga perkalian ε menjadi unsur non-Archimedes.[42] Namun, sebagai perluasan bilangan real, bilangan dual masih memiliki identitas 0,999…=1. Selain itu, manakala ε terdapat dalam bilangan dual, begitu pula dengan ε/2, sehingga ε bukanlah "bilangan dual positif paling kecil yang memungkinkan". Dalam bilangan real, tidak terdapat bilangan seperti itu. Analisis nonstandar dapat memberikan kita suatu sistem bilangan dengan susunan penuh infinitesimal (dan balikannya).[43] A.H. Lightstone mengembangkan ekspansi desimal non standar untuk bilangan real dalam (0, 1)∗.[44] Lightstone menunjukkan bagaimana kita dapat mengasosiasikan tiap-tiap bilangan real yang diperluas ke sebuah barisan digit yang diindeks menggunakan bilangan asli yang diperluas. Walaupun ia tidak secara langsung mendiskusikan bilangan 0,999..., ia menunjukkan bahwa bilangan real 1/3 diwakili oleh 0,333...;...333..., yang merupakan konsekuensi dari prinsip transfer. Dengan mengalikannya dengan 3, kita mendapatkan fakta bahwa hal ini juga berlaku bagi ekspansi desimal dengan 9 berulang. Lightstone menunjukkan bahwa dalam sistem in, ekspresi "0,333...;...000..." dan "0,999...;...000..." tidak memiliki padanan ke bilangan apapun. Bilangan p-adicKetika ditanyakan mengenai 0,999..., para pemula sering kali percaya bahwa bilangan ini haruslah memiliki angka "9 paling akhir" dan percaya bahwa 1 − 0,999... adalah bilangan positif yang dapat ditulis sebagai "0,000...1". Tak peduli apakah hal ini masuk akal, alasan dari pemikiran ini adalah sangat jelas: dengan menambahkan angka "1" pada digit "9" terakhir pada 0,999... akan membuat semua "9" menjadi "0" dan menghasilkan nilai 1. Namun pemikiran ini tidak dapat diterapkan karena ketiadaan angka "9 terakhir" pada bilangan 0,999....[45] Walaupun demikian, terdapat suatu sistem bilangan alternatif yang mengandung barisan angka 9 tak terhingga namun memiliki angka 9 yang terakhir. 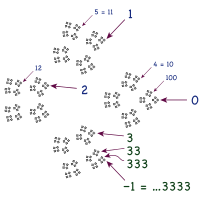 Bilangan p-adic adalah sistem bilangan alternatif dalam teori bilangan. Seperti bilangan real pada umumnya, bilangan p-adic dapat dibangun dari bilangan rasional melalui barisan Cauchy. Konstruksi ini memiliki sistem yang berbeda, yakni 0 lebih dekat dengan p, dan lebih dekat lagi dengan pn, daripada dengan 1. Bilangan p-adic membentuk medan untuk p prima dan cincin untuk p lainnya. Dalam bilangan 10-adic, analogi untuk ekspansi desimalnya berjalan ke arah kiri. Ekspansi bilangan 10-adic ...999 memiliki angka 9 terakhir dan tidak memiliki angka 9 paling awal. Seseorang dapat menambahkan angka 1 pada posisi 9 terakhir, dan ia akan menyebabkan bilangan ini menjadi berangka 0 sampai tak terhingga: 1 + ...999 = ...000 = 0, sehingga ...999 = −1.[46] Kita juga dapat menurunkannya menggunakan deret geometri. Deret tak terhingga yang diimplikasikan oleh "...999" tidak berkonvergen ke bilangan real manapun, tetapi ia berkonvergen kepada bilangan 10-adic, sehingga kita dapat menggunakan rumus: Oleh karena 0,999... = 1 (dalam sistem bilangan real) dan ...999 = −1 (dalam bilangan 10-adic), maka berdasarkan "keyakinan buta dan penyulapan simbol-simbol"[48] seseorang dapat menambahkan kedua persamaan tersebut dan berakhir pada ...999,999... = 0. Persamaan ini tidak masuk akal baik sebagai ekspansi 10-adic maupun sebagai ekspansi desimal yang biasa. Namun ini akan menjadi sangat bermakna dan betul apabila kita mengembangkan "teori desimal ganda".[49] Catatan kaki
Referensi
Pranala luarWikimedia Commons memiliki media mengenai 0.999….
|























