|
Sistem bilangan biner
Sistem bilangan biner adalah suatu notasi posisional dengan nilai basis 2. Setiap digit pada sistem ini disebut bit (binary digit). Karena penerapannya yang mudah sebagai gerbang logika dalam rangkaian-rangkaian elektronik, sistem biner digunakan oleh hampir semua perangkat komputer dan berbasis-komputer karena kesederhanaan bahasa dan kekebalannya terhadap derau (noise) dalam penerapan dunia nyata.[1] SejarahSistem bilangan binear modern dipelajari di Eropa pada abad ke-16 dan 17, oleh para matematikawan meliputi Thomas Harriot, Juan Caramuel y Lobkowitz, dan Gottfried Leibniz. Akan tetapi, sistem-sistem yang berkaitan dengan bilangan biner sudah muncul di banyak budaya kuno, seperti Mesir, China, dan India. Mesir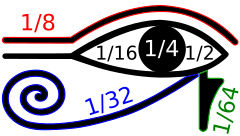 Para ahli tulis Mesir kuno menggunakan dua sistem kepenulisan yang berbeda untuk bilangan pecahan, yakni pecahan Mesir (tidak ada kaitan dengan sistem bilangan biner) dan pecahan Mata Horus (disebut demikian karena banyak sejarawan matematika percaya bahwa simbol-simbol yang digunakan dalam sistem ini dapat disusun untuk membentuk mata Horus, meskipun hal ini masih diperdebatkan).[2] Pecahan Mata Horus adalah sistem bilangan biner untuk besaran-besaran pecahan dari biji-bijian, cairan, dan ukuran lainnya; dalam sistem ini satu hekat dinyatakan sebagai jumlah dari pecahan biner 1/2, 1/4, 1/8, 1/16, 1/32, dan 1/64. Bentuk awal dari sistem ini dapat ditemukan dalam dokumen-dokumen dari Dinasti kelima Mesir, sekitar 2400 SM, dan bentuk hieroglif modernnya berasal dari Dinasti kesembilan belas Mesir, sekitar 1200 SM.[3] ChinaMasa klasikIndiaAfrikaKebudayaan lainEropa pra-LeibnizLeibnizPerkembangan selanjutnyaKepenulisanMencacah dalam binerMencacah dalam sistem desimalpendahuluan Mencacah dalam sistem binerPecahanAritmetika binerPenambahanPenguranganPerkalianPembagianAkar kuadratOperasi bitwiseKonversi dari dan ke sistem bilangan lainnya
Dari Biner ke Desimal Untuk setiap bilangan biner dengan digit: dn-1, ... d3, d2, d1, d0 Bilangan desimalnya adalah hasil penjumlahan dari digit biner () dikalikan dengan pangkat 2 nya (): decimal = d0 × 20 + d1 × 21 + d2 × 22 + ... Contoh: Tabel dibawah ini menunjukkan konversi bilangan biner 01010101 menjadi desimal.
Diperoleh hasil akhir bahwa 010101012 = 8510. Dari Desimal ke Biner
Desimal = 10 Bilangan yang mendekati 10 adalah 8 (23), selanjutnya hasil pengurangan 10-8 = 2 (21), sehingga dapat dijabarkan seperti berikut: 10 = (1 x 23) + (0 x 22) + (1 x 21) + (0 x 20) Dari perhitungan di atas bilangan biner dari 10 adalah 1010. Dapat juga dengan cara lain yaitu 10: 2 = 5 sisa 0 (0 akan menjadi angka terakhir dalam bilangan biner), 5 (hasil pembagian pertama): 2 = 2 sisa 1 (1 akan menjadi angka kedua terakhir dalam bilangan biner), 2 (hasil pembagian kedua): 2 = 1 sisa 0 (0 akan menjadi angka ketiga terakhir dalam bilangan biner), 1(hasil pembagian ketiga): 2 = 0 sisa 1 (1 akan menjadi angka pertama dalam bilangan biner) karena hasil bagi sudah 0 atau habis, sehingga bilangan biner dari 10 = 1010. Atau dengan cara yang singkat: 10:2=5(0), 5:2=2(1), 2:2=1(0), 1:2=0(1) sisa hasil bagi dibaca dari belakang menjadi 1010. Desimal ke binerBiner ke desimalHeksadesimalOktalMerepresentasikan bilangan riilContoh penerapanPengenalan Warna Citra BinerCitra biner (binary image) adalah citra yang hanya mempunyai dua nilai derajat: Meskipun saat ini citra berwarna lebih disukai karena memberi kesan yang lebih kaya daripada citra biner, namun tidak membuat citra biner mati. Pada beberapa aplikasi citra biner masih tetap dibutuhkan, misalnya citra logo instansi (yang hanya terdiri atas warna hitam dan putih), citra kode batang (bar code) yang tertera pada label barang, citra hasil pemindahan dokumen teks, dan sebagainya. objek di dalam citra biner adalah segmentasi objek. Proses segmentasi bertujuan mengelompokkan pixel-pixel objek menjadi wilayah (region) yang merepresentasikan objek. Ada dua pendekatan yang digunakan dalam segmentasi objek:
Pranala luarWikimedia Commons memiliki media mengenai Binary numeral system. Wikibooks memiliki buku di:
Referensi
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



