在同調代數中,蛇引理是構造長正合序列的關鍵工具,此引理在任何阿貝爾範疇中皆成立。依此構造的同態通常稱作連結同態。
敘述
考慮一阿貝爾範疇 (例如阿貝爾群或模的範疇)中的交換圖:
(例如阿貝爾群或模的範疇)中的交換圖:

使得每一橫列均為正合序列。此時存在一個聯繫 的核與上核的正合序列:
的核與上核的正合序列:

此外,若 是單射,則
是單射,則 亦然;若
亦然;若 是滿射,則
是滿射,則 亦然。
亦然。
引蛇出洞
為了理解蛇引理的由來,觀察下圖:
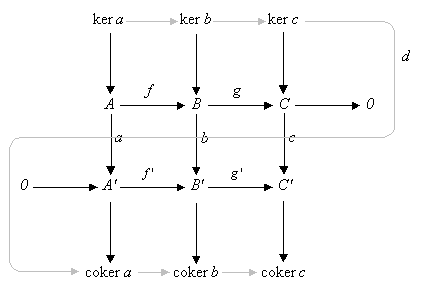
並注意到:引理給出的正合序列可在此圖中畫成倒S狀的蛇形。
構造連接同態
核間的同態與上核間的同態很容易構造,它們由該圖的交換性自然導出,正合性也可以直接代定義驗證。重點在於連接同態 及序列在該處的正合性。
及序列在該處的正合性。
對於模範疇的情形,同態 可如是構造:
可如是構造:
選定 ,並視之為
,並視之為 的元素;由於
的元素;由於 是滿射,存在
是滿射,存在 滿足
滿足 。由圖的交換性,我們有
。由圖的交換性,我們有
 (因為
(因為 )
)
於是 。由於底部的橫列正合,存在
。由於底部的橫列正合,存在 使得
使得 。置
。置 。今須驗證
。今須驗證 是明確定義的,即
是明確定義的,即 不依賴
不依賴 之選取;此外尚須驗證它是個同態,及序列的正合性。
之選取;此外尚須驗證它是個同態,及序列的正合性。
一旦完成以上幾點驗證,即證明了此引理在模範疇的情形。對一般情形,可利用核與上核的泛性;此外也能使用Mitchell嵌入定理,此定理斷言任一阿貝爾範疇都能遷入某個環 的
的 -模範疇。
-模範疇。
函子性
在應用上,我們常常需要長正合列的「函子性」或曰「自然性」(就自然變換意義言之);各種建構的函子性也是同調代數的基本哲學。此函子性可由蛇引理的函子性導出。
設交換圖
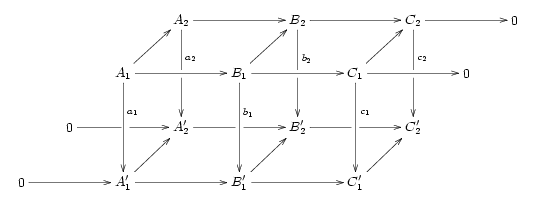
的橫列均為正合,則可利用蛇引理兩次,一次在「前」一次在「後」,產生兩條長正合序列;它們經由以下交換圖相連繫:

文獻
- Serge Lang, Algebra (2002), Graduate Texts in Mathematics 211, Springer. ISBN 0-387-95385-X
























