同調代數

同調代數是數學的一個分支，它研究同調與上同調技術的一般框架。

簡述

同調代數是一門相對年輕的學科，其源頭可追溯到代數拓撲（單純形同調）與抽象代數（合衝模）在十九世紀末的發展，這兩門理論各自由龐加萊與希爾伯特開創。

同調代數的發展與範疇論的出現密不可分。大致說來，同調代數是（上）同調函子及其代數結構的研究。「同調」與「上同調」是一對對偶的概念，它們滿足的範疇論性質相反（即：箭頭反向）。數學很大一部分的內在構造可藉鏈複形理解，其性質則以同調與上同調的面貌展現，同調代數能萃取這些鏈複形蘊含的資訊，並表之為拓撲空間、層、群、環、李代數與C*-代數等等「具體」對象的（上）同調不變量。譜序列是計算這些量的有力工具。

同調代數肇始即在代數拓撲中扮演要角。其影響日漸擴大，目前已遍及交換代數、代數幾何、代數數論、表示理論、算子代數、偏微分方程與非交換幾何。K-理論是一門獨立的學科，它也採用同調代數的辦法。

主要對象：鏈複形

主条目：鏈複形

同調代數領域的基本對象是一個鏈複形${\displaystyle (A_{\bullet },d_{\bullet })}$。這是一個由交換群、模或更廣義地說是由一個阿貝爾範疇的對象組成的序列A₀, A₁, A₂……。它們通過一系列同態d_n : A_n→A_n-1相連，使得每兩個連接的映射的合成 為零：對所有n有d_n o d_n+1 = 0（有時逕寫作${\displaystyle d^{2}=0}$）

${\displaystyle \ldots \to A_{n+1}{\begin{matrix}d_{n+1}\\\to \\\,\end{matrix}}A_{n}{\begin{matrix}d_{n}\\\to \\\,\end{matrix}}A_{n-1}{\begin{matrix}d_{n-1}\\\to \\\,\end{matrix}}A_{n-2}\to \ldots \to A_{2}{\begin{matrix}d_{2}\\\to \\\,\end{matrix}}A_{1}{\begin{matrix}d_{1}\\\to \\\,\end{matrix}}A_{0}{\begin{matrix}d_{0}\\\to \\\,\end{matrix}}0}$。

鏈複形的同調群定義為：

${\displaystyle H_{i}(A_{\bullet }):=\mathrm {Ker} (d_{i})/\mathrm {Im} (d_{i+1})}$

• 同調群皆為零的鏈複形稱作正合的。
• 兩個鏈複形${\displaystyle (A_{\bullet },d_{A,\bullet })}$、${\displaystyle (B_{\bullet },d_{B,\bullet })}$之間的鏈映射是一族同態${\displaystyle f_{n}:A_{n}\rightarrow B_{n}}$，使之滿足：${\displaystyle f_{n}\circ d_{A,n}=d_{B,n}\circ f_{n+1}}$；全體鏈複形依此構成一範疇。鏈映射誘導出同調群的映射。
• 對鏈映射可以定義同倫的概念，這是拓撲學的同倫在代數框架下的翻譯。同倫的鏈映射在同調群上誘導出相同的映射。
• 在同調群上誘導出同構的鏈映射稱作擬同構。

鏈複形概念的一個對偶版本是上鏈複形。一個上鏈複形${\displaystyle (A^{\bullet },d^{\bullet })}$是個序列A^0, A^1, A^2……。它們由一系列同態d^n : A^n→A^n+1相連，使得任何兩個接連的映射的合成為零：對所有n有d^n+1 o d^n = 0：

${\displaystyle 0\to A^{0}{\begin{matrix}d^{0}\\\to \\\,\end{matrix}}A^{1}{\begin{matrix}d^{1}\\\to \\\,\end{matrix}}A^{2}\to \ldots \to A^{n-1}{\begin{matrix}d^{n-1}\\\to \\\,\end{matrix}}A^{n}{\begin{matrix}d^{n}\\\to \\\,\end{matrix}}A^{n+1}\to \ldots }$。

關於鏈複形的種種定義可以照搬至上鏈複形；實質上，我們僅須將原定義中的所有箭頭反轉。例如上鏈複形的上同調群定義為：

${\displaystyle H^{i}(A^{\bullet }):=\mathrm {Ker} (d^{i})/\mathrm {Im} (d^{i-1})}$

形式地說，同調代數可定義為鏈複形與上鏈複形的抽象研究。以下我們將看到它的具體根源。

溯源

代數拓撲學的黎明

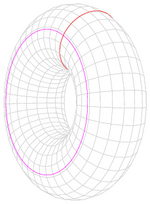
環面上的兩種閉曲線，它們都無法表成區域的邊界。

同調代數的根源之一在代數拓撲，而後者的歷史則可上溯至十九世紀中。早在黎曼關於阿貝爾簇的工作中，就已考慮過黎曼曲面上的閉曲線是否為一塊區域的邊界的問題；根據斯托克斯定理，閉形式在這類閉曲線上的積分恆為零，而這類曲線的多寡顯然牽涉到曲面的拓撲性狀。黎曼依此定義了「連通數」——用現代的語言表述即是${\displaystyle 1+\dim H_{1}(X;\mathbb {Z} /2\mathbb {Z} )}$，此量關係到黎曼曲面的虧格，直觀地理解便是曲面上有幾個「洞」。

龐加萊在1895年的經典論文Analysis Situs及其後續工作真正奠定了代數拓撲學的基礎。他考慮的對象是後來所謂的單純複形，這類空間在同胚的意義下可剖分為多面體，它包含了微分拓撲中處理的大多數有限維空間。龐加萊考慮一個單純複形${\displaystyle X}$中各種維度的單純形（零維的點、一維的線、二維的三角形、三維的四面體等等）的整係數線性組合，稱之為鏈，它們構成一系列的阿貝爾群${\displaystyle C_{0}(X),C_{1}(X),C_{2}(X),\ldots }$，其中下標代表維度。龐加萊還定義了一個邊界映射${\displaystyle \partial _{i}:C_{i}(X)\rightarrow C_{i-1}(X)}$，它在單純形上的作用是將${\displaystyle i}$維單純形的${\displaystyle (i-1)}$維邊界取適當正負號後作線性組合；彼此差個邊界的鏈在拓撲上稱作同調的，這也是同調代數的詞源。龐加萊證明${\displaystyle \partial _{i-1}\circ \partial _{i}=0}$，於是我們有以下鏈複形

${\displaystyle \cdots \longrightarrow C_{i}(X){\stackrel {\partial _{i}}{\longrightarrow }}C_{i-1}\longrightarrow \cdots {\stackrel {\partial _{1}}{\longrightarrow }}C_{0}(X)\longrightarrow 0}$

定義${\displaystyle X}$的貝蒂數與歐拉示性數：

• ${\displaystyle b_{i}(X):=\dim {\dfrac {\mathrm {Ker} (\partial _{i})}{\mathrm {Im} \partial _{i+1}}}\otimes \mathbb {Q} }$
• ${\displaystyle \chi (X):=\sum _{i}(-1)^{i}b_{i}=\sum _{i}(-1)^{i}\dim C_{i}(X)\otimes \mathbb {Q} }$

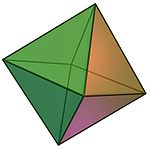
單純複形的例子：八面體，它有6個頂點、12個邊和8個面

這兩個量都與空間${\displaystyle X}$的剖分方式無關，僅決定於空間的倫型。起初龐加萊只考慮數值不變量；在1925年，埃米·诺特於一份只有14行的報告中指出：根本的不變量是阿貝爾群${\displaystyle H^{i}(X)=\mathrm {Ker} (\partial _{i})/\mathrm {Im} \partial _{i+1}}$，而不僅僅是它派生的非負整數${\displaystyle b_{i}=\dim H^{i}(X)\otimes \mathbb {Q} }$；群結構能給出更細的拓撲資訊，而空間的連續映射能導出同調群的同態。代數拓撲的風貌從此遂澈底改變。

循此脈絡，L. Mayer在1929年定義了抽象的鏈複形及其同調群。同調理論自此有了純代數的框架。

隨後十年間，數學家們為各種空間定義了形形色色的同調與上同調，例如在德拉姆上同調中，我們設${\displaystyle \Omega ^{i}(M)}$為光滑流形${\displaystyle M}$上的${\displaystyle i}$次微分形式，同態${\displaystyle d^{i}:\Omega ^{i}(M)\rightarrow \Omega ^{i+1}(M)}$定義為外微分。無論哪種理論，對同一空間總是給出相同的同調群；塞缪尔·艾伦伯格與诺曼·斯廷罗德在1945年以公理化方法梳理拓撲空間的（上）同調理論，從而證明先前種種理論只是同一個對象的不同面貌。此時同調代數儼然已自成一格了。

此後拓撲學仍不斷為同調代數注入動力，例子包括了：

• 万有系数定理：關係到函子${\displaystyle \mathrm {Tor} _{1}(-,-)}$與${\displaystyle \mathrm {Ext} ^{1}(-,-)}$。這個定理告訴我們如何從係數為${\displaystyle \mathbb {Z} }$的（上）同調群決定任意係數的情形。
• 非球空間的上同調群：它們可由基本群的群上同調算出，這也是一種Ext函子。
• 李群的上同調群：由其李代數決定，由此催生了李代數上同調理論。

希爾伯特與合衝模

同調代數的另一條線索可以追溯到十九世紀的顯學不變量理論與大衛·希爾伯特。希爾伯特為了研究不變量本身、不變量間的關係、以及關係間的關係……，而考慮自由分解的問題：設${\displaystyle A}$為諾特環，${\displaystyle M}$為有限生成的${\displaystyle A}$-模，

希爾伯特基底定理（1888年）。存在正整數${\displaystyle n_{0}}$及滿態射${\displaystyle \phi _{0}:A^{n_{0}}\rightarrow M}$。

設${\displaystyle M_{1}:=\mathrm {Ker} (\phi _{0})}$，則${\displaystyle 0\longrightarrow M_{1}\longrightarrow A^{n_{0}}{\stackrel {\phi _{0}}{\longrightarrow }}M\longrightarrow 0}$是${\displaystyle M}$的一個有限展示；${\displaystyle M_{1}}$稱作第一個合衝模（syzygy）。

另一方面，${\displaystyle M_{1}}$也是有限生成的，於是存在另一個有限展示

${\displaystyle 0\longrightarrow M_{2}\longrightarrow A^{n_{1}}{\stackrel {\phi _{1}}{\longrightarrow }}M_{1}\longrightarrow 0}$

${\displaystyle M_{2}}$稱作第二個合衝模。反覆操作遂得到一個${\displaystyle A}$-模的鏈複形：

${\displaystyle \cdots \rightarrow A^{n_{i}}\rightarrow A^{n_{i-1}}\rightarrow \cdots \rightarrow A^{n_{1}}\rightarrow A^{n_{0}}\rightarrow M\rightarrow 0}$

其中每個同態的核都是前一個同態的像；用現代語言來說，這乃是${\displaystyle M}$的一個自由分解，長度最短的自由分解稱作極小分解。自由分解的好處在於：自由模的不變量很容易計算，而透過自由分解又能適當地拼合各個${\displaystyle A^{n_{i}}}$上的資訊，從而推出${\displaystyle M}$的代數性質。這是同調代數的基本技術之一。

希爾伯特合衝定理（1890年）。上述分解在有限步之內停止；換言之，存在夠大的${\displaystyle N}$使得第${\displaystyle N}$個合衝模${\displaystyle M_{N}}$是自由模。當${\displaystyle k}$是域而${\displaystyle A:=k[X_{1},\ldots ,X_{n}]}$時，極小分解的長度不大於${\displaystyle n}$。

希爾伯特藉著一個分次版的合衝定理證明了：在同樣條件下，一個有限生成分次模的希爾伯特函數是個多項式；他藉此闡明了不變量的個數對次數的關係。希爾伯特考慮的自由分解是投射分解的特例；在現代的同調代數理論中，投射分解及內射分解是定義導函子的基礎。

當${\displaystyle A}$是局部環時，極小分解的長度稱作${\displaystyle M}$的投射維度，它相當於使下式成立的最小整數${\displaystyle n}$：

${\displaystyle \forall N,i>n,\Rightarrow \mathrm {Ext} _{A}^{i}(M,N)=0}$

對所有${\displaystyle A}$-模的投射維度取極大值，得到的數稱為同調維度；同調維度等於${\displaystyle \dim A}$若且唯若${\displaystyle A}$是正則局部環；在這個意義下，可以說極小分解反映了幾何性質。合衝模也是計算代數幾何中的重要方法。

嘉當-艾倫伯格革命

昂利·嘉當與塞缪尔·艾伦伯格在1956年出版的著作Homological Algebra標示了同調代數的成熟。書中的概念與工具影響之深廣，成為各領域數學家們不可須臾離的生活資料。以下舉出數點例子：

• 投射模與內射模
• 左正合函子與右正合函子
• 投射分解與內射分解，並由此定義一個函子的導函子。
• 將Tor函子與Ext函子分別定義為${\displaystyle M\otimes _{R}-}$與${\displaystyle \mathrm {Hom} _{R}(-,M)}$的右導函子與左導函子，並探討了同調維度。
• 介紹了譜序列，並用以計算Tor與Ext。
• 鏈複形的嘉當-艾倫伯格分解與超上同調，可視為導範疇的濫觴。

一直到1970年代，嘉當與艾倫伯格的著作都是同調代數的聖經，同時期受歡迎的教本還有麦克兰恩的Homology，格羅滕迪克的《代數幾何基礎》與東北論文。

嘉當在1980年接受牛津大學榮譽博士時，曾用拉丁文寫下這麼一段話：

……utinam intelligere possim rationacinationes pulcherrimas quae e propositione concisa DE QUADRATUM NIHILO EXAEQUARI fluunt……

但願吾能領會${\displaystyle d^{2}=0}$此簡潔公式之美妙推論[1]

格羅滕迪克的東北論文

更多信息：阿貝爾範疇

亞歷山大·格羅滕迪克在1955年左右對韋伊猜想發生興趣，而真正勾動他的是此猜想的上同調表述；格羅滕迪克為此開始研習同調代數，當時嘉當-艾倫伯格的書尚未出版。嘉當與艾倫伯格僅考慮模構成的範疇。格羅滕迪克在1956年一封給塞爾的信中寫道：

我了解到，如果能在比模更廣的範疇上制定導函子理論，則可輕易獲得空間的上同調。存在性來自一個一般的判準，而細層將扮演內射模的角色。基本譜序列將成為一些有用且可愛的一般譜序列的特例。但我不確定這在不可分空間上管不管用，而且我也想起你懷疑維度${\displaystyle \geq 2}$時是否存在上同調正合序列。也許這在嘉當-艾倫伯格的書裡多少都有明確表述，但我還無緣一讀。（1955年2月26日）[2]

這封信鋪陳了後來所謂東北論文[3]的梗概。空間的上同調係指層上同調，當時是以Čech上同調或細層分解定義的；而所謂細層是一類帶有單位分解的層，因此只在仿緊空間（當時稱作可分空間）上有細層分解；這對微分幾何與複幾何不成問題，但對一般的代數簇則是致命缺陷。塞爾回覆道：

“嘉當-艾倫伯格的書中並未以導函子演繹層上同調（至少在仿緊的情形）。嘉當意識到這個問題，並吩咐Buchsbaum去做，但看來他還沒做出來。主要的興趣應在於找出我們需要的細層性質，依此可以判斷不可分空間上是否有夠多細層（我想答案是否定的，但我一點也不確定！）。”（1955年3月12日）[4]

格羅滕迪克遂著手重寫同調代數的基礎。

這條思路在他於1957年發表於《東北數學雜誌》的論文Sur quelques points d'algèbre homologique[3]中開花結果。原本區區數頁的簡單定義變為102頁的範疇論論證，謠傳他因此花了兩年才找到地方刊登；但後續發展證明他的努力與收穫是相稱的。論文提出的重要觀念如下：

• 阿貝爾範疇的公理
• δ-函子與泛δ-函子
• 相對於一個函子的非循環對象：例如仿緊空間上的細層之於截面函子。
• 格羅滕迪克譜序列：涉及如何計算合成函子的導函子，可從此導出嘉當-艾倫伯格書中的許多譜序列與拓撲學中的Leray譜序列。

格羅滕迪克藉此將層上同調化為導函子的特例，阿貝爾範疇也成為同調代數的標準語言。

導範疇

更多信息：導範疇

八角形公理圖解，它是三角範疇最難理解的公理之一。

格羅滕迪克在1961年左右面臨一個技術瓶頸：為了為任意概形上的凝聚層建立對偶定理，必須為同調代數發展新工具。這個任務由他的學生讓-路易·韋迪耶（Jean-Louis Verdier）完成了。

Verdier在1967年的博士論文Des Catégories Dérivées des Catégories Abéliennes中引入了三角範疇與導範疇的觀念。約略地說，三角範疇是一種能製造長正合序列與上同調函子的範疇；一個阿貝爾範疇${\displaystyle {\mathcal {A}}}$上的鏈複形範疇${\displaystyle C({\mathcal {A}})}$便是一例。其次，我們等同${\displaystyle C({\mathcal {A}})}$中同倫等價的態射，從而得到商範疇${\displaystyle K({\mathcal {A}})}$，它仍然具備三角範疇的結構；最後，建構${\displaystyle K({\mathcal {A}})}$對擬同構的局部化以獲得導範疇${\displaystyle D({\mathcal {A}})}$，換言之即是為所有擬同構添加逆態射。

假設${\displaystyle {\mathcal {A}}}$有夠多內射元，則在導範疇裡同樣可以定義左正合函子${\displaystyle F}$的右導函子${\displaystyle RF(-)}$，它與古典定義${\displaystyle R^{n}F(-)}$的關係由下式給出：

${\displaystyle H^{n}(RF(X))=R^{n}F(X)}$

假設左正合函子${\displaystyle G}$將內射對象映至${\displaystyle F}$的非循環對象，此時格羅滕迪克譜序列化作格外簡明的形式：

${\displaystyle (R^{+}F)\circ (R^{+}G)=R^{+}(F\circ G)}$

對右正合函子也有相應的結果。儘管譜序列在導範疇的進路中不是那麼根本，但在具體計算時仍佔一席之地。

Verdier藉這套語言證明了Verdier對偶定理，這是龐加萊對偶定理的深遠推廣，適用於任何局部緊有限維拓撲空間。導範疇的應用仍在不斷擴大中；在代數幾何之外，導範疇理論的最大成功之一是證明了任意維度的黎曼-希爾伯特對應。

Verdier的博士論文直到1996年才出版，此前導範疇的第一手資料是由他執筆的SGA 4½末章：Catégories dérivées (état 0)。

單純形法

龐加萊研究拓撲的方法是將空間剖分為多面體，這時空間的拓撲性質完全決定於這些點、線、面……等等[「單純形」及其間的相交關係。將這套方法抽象化，便可對任何範疇${\displaystyle {\mathcal {A}}}$定義單純形對象（及其對偶上單純形對象）。在${\displaystyle {\mathcal {A}}}$為集合範疇的情形特別有用，此時的單純形對象稱為單純形集合（及其對偶上單純形集合）。對單純形集合可定義其幾何實現，這是一個CW-複形。對於來自一個源自拓撲空間的單純形集合，幾何實現不外是將空間「拼回去」；而對源於代數構造的單純形集，幾何實現則能用以構造分類空間。在單純形集合上可以抽象地開展同倫論的研究。

另一方面，若取${\displaystyle {\mathcal {A}}}$為一阿貝爾範疇，對任一單純形對象${\displaystyle A}$皆可定義一個鏈複形${\displaystyle N(A)}$。此時單純形對象與鏈複形的關係由以下定理闡明：

Dold-Kan對應定理（1957年）。函子${\displaystyle N}$給出範疇間的等價

{${\displaystyle {\mathcal {A}}}$中的單純形對象} ${\displaystyle {\stackrel {\sim }{\longrightarrow }}{\mathcal {C}}^{+}({\mathcal {A}}):=}$ { ${\displaystyle {\mathcal {A}}}$上的鏈複形${\displaystyle C_{n}}$，並滿足${\displaystyle n<0\Rightarrow C_{n}=0}$ }

透過這個對應，單純形集合理論可助同調代數一臂之力，例如我們可藉此定義更廣義的導函子，或得到某類對象的典範分解。

非交換理論

源於同調論的古典同調代數只給出「可交換」的資訊。對於空間${\displaystyle X}$上的非交換群層${\displaystyle G}$，古典方法只能定義第一個上同調${\displaystyle H^{1}(X;G)}$；這個集合分類了${\displaystyle X}$上的扭子。數學家們嘗試定義高階的非交換上同調，這方面的理論常牽涉到同倫理論、單純形集合，或者高階的範疇論（如疊論）。

同調代數與同倫代數

就模型範疇的觀點，同調代數可被視為同倫理論的一支。這是Daniel Quillen將模型範疇理論稱作同倫代數的原因 。

參考資料

1. 見文獻Methods of Homological Algebra, Preface
2. 見文獻Correspondance Grothendieck-Serre, pp.13-14
3. Grothendieck, A., Sur quelques points d’algèbre homologique, Tôhoku Mathematical Journal, (2), 1957, 9: 119–221 [2017-11-06], MR 0102537, doi:10.2748/tmj/1178244839, （原始内容存档于2020-08-20） . English translation （页面存档备份，存于互联网档案馆）
4. 見文獻Correspondance Grothendieck-Serre, p.15

外部連結

• Colin McLarty, The Rising Sea: Grotendieck on simplicity and generality I
• Colin MacLarty, Emmy Noether's Set-Theoretic Topology: From Dedekind to the first functors
• Charles Weibel, A History of Homological Algebra
• V.E. Govorov A.V. Mikhalev, Homological Algebra, Hazewinkel, Michiel (编), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 

文獻

• Henri Cartan, Samuel Eilenberg, Homological algebra. Reprint of the 1956 original. Princeton Landmarks in Mathematics. Princeton University Press, Princeton, NJ, 1999. xvi+390 pp. ISBN 0-691-04991-2
• Deligne, Pierre; ed. Séminaire de Géométrie Algébrique du Bois Marie - Cohomologie étale -（SGA 4½）（1977）, Lecture notes in mathematics 569), Berlin; New York: Springer-Verlag, iv+312.
• Alexander Grothendieck, Sur quelques points d'algèbre homologique. Tôhoku Math. J.（2）9, 1957, 119--221
• Gelfand, Sergei I.; Yuri Manin, Methods of homological algebra. Translated from Russian 1988 edition. Second edition. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. xx+372 pp. ISBN 3-540-43583-2
• Weibel, Charles A., An introduction to homological algebra. Cambridge Studies in Advanced Mathematics, 38. Cambridge University Press, Cambridge, 1994. xiv+450 pp. ISBN 0-521-43500-5; 0-521-55987-1
• Verdier, Jean-Louis, Des Catégories Dérivées des Catégories Abéliennes（1996）, Astérisque 239.