Set 類型 卡片遊戲 玩家數目 2人以上 所需技巧 視覺、邏輯思考、專心 牌的數量 81 遊戲時間 10-30分鐘
一組Set,三張牌的數字、圖案、顏色及紋路都不同,因此可組成Set 神奇形色牌 (Set )是由Marsha Falco在1974年發明的卡片遊戲 ,由Set企業 [ 1]
此遊戲是作者在擔任遺傳學家 時,由一個編碼系統衍生而來[ 2] 門薩學會 的門薩首選 ,在1995年德國玩家票選最佳遊戲
玩神奇形色牌 神奇形色牌的核心是組成Set的條件,只要桌面任意三張牌符合以下所有的條件,即為一個Set:
三張牌的數字相同,或是三張牌的數字完全不同。
三張牌的圖案相同,或是三張牌的圖案完全不同。
三張牌的紋路相同,或是三張牌的紋路完全不同。
三張牌的顏色相同,或是三張牌的顏色完全不同。 若有二張牌的特徵相同,但另一張牌和另外二張不同,這三張牌不能組成Set。
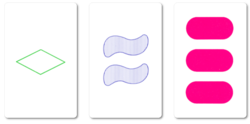
例如,以下的三張牌可以組成Set:
一個紅色實心菱形
二個紅色條紋菱形
三個紅色空心菱形 任選81張牌中的二張牌,都可以在剩下79張牌中找到一張牌,和前面的二張組成Set。
在標準的神奇形色牌遊戲中,發牌者將十二張牌放在桌上,若任一遊戲者找到一組Set,即可喊Set,並將三張牌拿走,發牌者將桌上的牌補足 ,到12張(若遊戲者喊了Set,但沒辦法很快的將三張牌拿走,會被處罰)。有可能十二張中都沒有三張牌可以組成Set,發牌者可以再發牌到15張,使讓遊戲者繼續找Set,若有需要可以再發牌到18張……。遊戲一直進行到所有的牌都發完,桌上沒有牌可以組成Set為止,此時拿到最多Set的遊戲者獲勝。
神奇形色牌也有很多不同的變體,其中包括不同的找Set方式,或是不同的遊戲者互動方式。也有許多狂熱的玩家繼續的創造遊戲的變體[ 3] [ 4]
任選兩張牌,只有一張牌可以和這兩張組成Set,因此任選三張牌,會組成Set的機率是1/79。.
若一直拿牌,拿到有其中有三張牌為Set為止,在拿到Set之前最多會拿到20張牌[ 5] A090245
有
(
81
2
)
3
=
81
×
80
2
×
3
=
1080
{\displaystyle {\frac {81 \choose 2}{3}}={\frac {81\times 80}{2\times 3}}=1080}
Set中有
d
{\displaystyle d}
4
−
d
{\displaystyle 4-d}
(
4
d
)
2
d
80
{\displaystyle {\frac {{4 \choose d}2^{d}}{80}}}
從81張牌中拿12張牌,可能的組合為
(
81
12
)
=
81
!
12
!
69
!
=
70724320184700
≈
7.07
×
10
13
{\displaystyle {81 \choose 12}={\frac {81!}{12!69!}}=70724320184700\approx 7.07\times 10^{13}}
一開始拿12張牌,其中沒有Set的機率是1/30,但後面的機會就快速的增加,第四回合時約為1/14,後續的二十回合慢慢上昇到1/13,因此大部份玩遊戲的時間中,拿12張牌沒有Set的機率是1/13到1/14之間[ 6]
在玩遊戲時,若發到15張牌,其中沒有Set的機率為1/88[ 6]
所有遊戲中只用到十二張牌,都沒有用到十五張牌的機率約為30%[ 6]
十二張牌中平均會有
(
12
3
)
⋅
1
79
≈
2.78
{\displaystyle {12 \choose 3}\cdot {\frac {1}{79}}\approx 2.78}
(
15
3
)
⋅
1
79
≈
5.76
{\displaystyle {15 \choose 3}\cdot {\frac {1}{79}}\approx 5.76}