杖头线

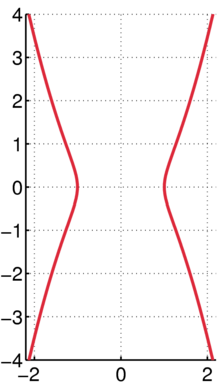
杖头线的圖，a = 1

杖头线（Kampyle of Eudoxus）是笛卡儿坐标系方程如下的曲線

${\displaystyle x^{4}=a^{2}(x^{2}+y^{2}),}$

但不包括x = y = 0的解。

另一種表示法

在極座標下，杖头线的方程如下

${\displaystyle r=a\sec ^{2}\theta .}$

其參數式為

${\displaystyle x=a\sec(t),\quad y=a\tan(t)\sec(t).}$

歷史

希臘天文學家及數學家歐多克索斯（c. 408 BC – c.347 BC）有研究此一四次曲線（英语：quartic curve），和求解經典的倍立方問題有關。

性質

杖头线對X軸及Y軸對稱，和X軸交點為(±a,0)，其拐点在

${\displaystyle \left(\pm a{\frac {\sqrt {6}}{2}},\pm a{\frac {\sqrt {3}}{2}}\right)}$

（四個拐点，每個象限各一個）。曲線上半部在${\displaystyle x\to \infty }$時漸近${\displaystyle x^{2}/a-a/2}$ as ${\displaystyle x\to \infty }$，可以寫成

${\displaystyle y={\frac {x^{2}}{a}}{\sqrt {1-{\frac {a^{2}}{x^{2}}}}}={\frac {x^{2}}{a}}-{\frac {a}{2}}\sum _{n=0}^{\infty }C_{n}\left({\frac {a}{2x}}\right)^{2n},}$

其中

${\displaystyle C_{n}={\frac {1}{n+1}}{\binom {2n}{n}}}$

是第${\displaystyle n}$個卡塔兰数。

參考資料

• J. Dennis Lawrence. A catalog of special plane curves. Dover Publications. 1972: 141–142. ISBN 0-486-60288-5. 

外部連結

• 約翰·J·奧康納; 埃德蒙·F·羅伯遜, Kampyle of Eudoxus, MacTutor数学史档案 （英语） 
• 埃里克·韦斯坦因. Kampyle of Eudoxus. MathWorld.